河南省商丘市柘城县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2021-04-16 类型:期末考试
一、填空题
-
1. 若二次根式 有意义,则x的取值范围是 .2. 已知直线 与 平行且经过点 ,则 的表达式是.3. 已知菱形的两条对角线长分别为4和9,则菱形的面积为.4. 如图,在矩形ABCD中,AC,BD相交于点O,AE平分 交BC于点E,若 ,则 .
 5. 若方程组 的解是 ,则直线y=﹣2x+b与直线y=x﹣a的交点坐标是.6. 某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)依次为95、90、88,则小彤这学期的体育成绩为分.7. 下列计算错误的是( )A、3+2 =5 B、 ÷2= C、 × = D、 =
5. 若方程组 的解是 ,则直线y=﹣2x+b与直线y=x﹣a的交点坐标是.6. 某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)依次为95、90、88,则小彤这学期的体育成绩为分.7. 下列计算错误的是( )A、3+2 =5 B、 ÷2= C、 × = D、 =二、选择题
-
8. 在一个直角三角形中,已知两直角边分别为6cm,8cm,则下列结论不正确的是( )A、斜边长为10cm B、周长为25cm C、面积为24cm2 D、斜边上的中线长为5cm9. 如图,▱ABCD中,对角线AC,BD相交于点O,OA=3,若要使平行四边形ABCD为矩形,则OB的长度为( )
 A、4 B、3 C、2 D、110. 下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差S2:
A、4 B、3 C、2 D、110. 下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差S2:甲
乙
丙
丁
平均数
 (cm)
(cm)175
173
175
174
方差S2(cm2)
3.5
3.5
12.5
15
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁11. 矩形、菱形、正方形都具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线互相平分且相等12. 已知正比例函数y=kx,且y随x的增大而减少,则直线y=2x+k的图象是( )A、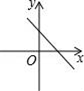 B、
B、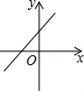 C、
C、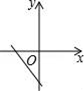 D、
D、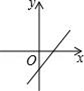 13. 如图,直线 与 的交点的横坐标为-2,则关于x的不等式 的整数解为( ).
13. 如图,直线 与 的交点的横坐标为-2,则关于x的不等式 的整数解为( ). A、-1 B、 C、-4 D、-314. 如图,平行四边形ABCD中, , , ,动点E从B点出发,沿 运动至A点停止,设运动的路程为x, 的面积为y,则y与x的函数关系用图象表示正确的是( )
A、-1 B、 C、-4 D、-314. 如图,平行四边形ABCD中, , , ,动点E从B点出发,沿 运动至A点停止,设运动的路程为x, 的面积为y,则y与x的函数关系用图象表示正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、
三、解答题
-
15. 计算:(1)、( + )( - )(2)、16. 如图,ABCD为任意四边形, 依次为各边中点,证明:四边形EFGH为平行四边形.
 17. 如图,折叠矩形ABCD的一边AD,使点D落在BC边上的点F处,折痕为AE,若BC=10cm,AB=8cm,求EF的长.
17. 如图,折叠矩形ABCD的一边AD,使点D落在BC边上的点F处,折痕为AE,若BC=10cm,AB=8cm,求EF的长. 18. 已知:如图,△OAB,点O为原点,点A、B的坐标分别是(2,1)、(﹣2,4).
18. 已知:如图,△OAB,点O为原点,点A、B的坐标分别是(2,1)、(﹣2,4). (1)、若点A、B都在一次函数y=kx+b图象上,求k,b的值;(2)、求△OAB的边AB上的中线的长.19.
(1)、若点A、B都在一次函数y=kx+b图象上,求k,b的值;(2)、求△OAB的边AB上的中线的长.19.正方形ABCD中,P为对角线BD上一点,PE⊥BC,垂足为E,PF⊥CD, 垂足为F,求证:EF=AP
 20. 某校要从王同学和李同学中挑选一人参加县知识竞赛在五次选拔测试中他俩的成绩如下表.
20. 某校要从王同学和李同学中挑选一人参加县知识竞赛在五次选拔测试中他俩的成绩如下表.第1次
第2次
第3次
第4次
第5次
王同学
60
75
100
90
75
李同学
70
90
100
80
80
根据上表解答下列问题:
(1)、完成下表:姓名
平均成绩(分)
中位数(分)
众数(分)
方差
王同学
80
75
75
李同学
(2)、在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则王同学、李同学在这五次测试中的优秀率各是多少?(3)、历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.21. 为改善生态环境,防止水土流失,某村计划在堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:甲林场
乙林场
购树苗数量
销售单价
购树苗数量
销售单价
不超过1000棵时
4元/棵
不超过2000棵时
4元/棵
超过1000棵的部分
3.8元/棵
超过2000棵的部分
3.6元/棵
设购买白杨树苗x棵,到两家林场购买所需费用分别为 (元)、 (元).则:
(1)、该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为元,若都在乙林场购买所需费用为元;(2)、分别求出 、 与x之间的函数关系式;(3)、如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?