江苏省泰州市兴化市2021届九年级下学期数学3月月考试卷
试卷更新日期:2021-04-16 类型:月考试卷
一、单选题
-
1. 一组数据4,10,12,14,则这组数据的平均数是A、9 B、10 C、11 D、122. 已知 ,则 的值为( )A、 B、2 C、3 D、3. 已知 是关于x的一元二次方程 的解,则 ( )A、 B、 C、 D、4. 若一个扇形的圆心角为90°,半径为6,则该扇形的面积为( )A、 B、 C、 D、5. 将抛物线 向右平移3个单位,再向上平移4个单位,得到的抛物线是( )A、 B、 C、 D、6. 如图,△ABC中,顶点A、B均在第二象限,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C',且△A'B'C'与△ABC的位似比为2:1,设点B的对应点B'的横坐标是3,则点B的横坐标是( )
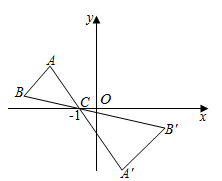 A、 B、﹣2 C、 D、﹣3
A、 B、﹣2 C、 D、﹣3二、填空题
-
7. 设x1 , x2是方程x2﹣3x+1=0的两个根,则x1•x2=.8. 如果4是a与8的比例中项,那么a的值为.9. 某中学为了选拔一名运动员参加市运会 米短比赛,有甲、乙两名运动员备选,他们最近测试的 次百米跑平均时间都是 秒,他们的方差分别是 (秒 ) (秒 ),如果要选择一名成绩优秀且稳定的人去参赛,应派去.10. 一个不透明的袋子中,袋中有1 个红球,2 个白球和3 个黑球,这些球除颜色外均相同,将球摇匀后,从袋子中任意摸出一个球,摸到(填“红”或“白”或“黑”)球的可能性最大.11. 已知两个相似三角形的相似比为4:9,那么这两个三角形的周长之比为.12. 如图, 、 、 、 为一个正多边形的顶点, 为正多边形的中心,若 ,则这个正多边形的边数为.
 13. 如图是一张长 ,宽 的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积 是的有盖的长方体铁盒.则剪去的正方形的边长为 .
13. 如图是一张长 ,宽 的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积 是的有盖的长方体铁盒.则剪去的正方形的边长为 .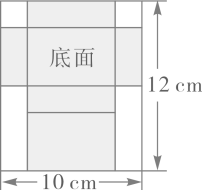 14. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是.
14. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是.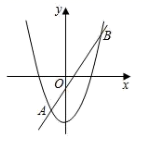 15. 如图,已知AB=BC= ,AC=4,点G为△ABC的重心,那么AG的长等于.
15. 如图,已知AB=BC= ,AC=4,点G为△ABC的重心,那么AG的长等于.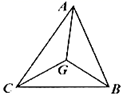 16. 如图,已知矩形ABCD,AB=2,AD=2 ,点E为对角线AC上一点(不与A、C重合),过点E作EF⊥DE交BC于点F,连接DF,则 的值等于.
16. 如图,已知矩形ABCD,AB=2,AD=2 ,点E为对角线AC上一点(不与A、C重合),过点E作EF⊥DE交BC于点F,连接DF,则 的值等于.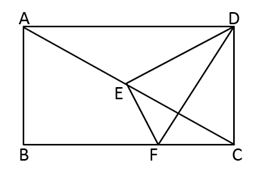
三、解答题
-
17.(1)、解方程: ;(2)、计算: .18. 已知抛物线 (m为常数).(1)、若抛物线与x轴只有一个公共点,求m的值;(2)、点 与 在抛物线 上,求m的值.19. 在不透明的口袋中装有 个白色、 个红色和若干个黄色的乒乓球(除颜外其余都相同),小明为了弄清黄色乒乓球的个数,进行了摸球的实验(每次只摸一个,记录颜色后放回,搅匀后重复上述步骤),下表是实验的部分数据:
摸球次数
摸到白球次数
摸到白球的概率
(1)、请你估计:摸出一个球恰好是白球的概率大约是(精确到 ),黄球有个;(2)、如果从上述口袋中,同时摸出 个球,求结果是一红一黄的概率.20. 中国教育科学研究院对全国 万个学生家庭进行的调查表明,孩子爱做家务的家庭比不爱做家务的家庭,孩子成绩优秀的比例高了 倍.为调查了解某区学生做家务的情况,随机发放调查表进行调查,要求被调查者从“A:不做家务,B:会煮饭或会做简单的菜,C:洗碗,D:保持自己的卧室清洁,E:洗衣服”五个选项中选择最常做的一项,将所有调查结果整理后绘制成不完整的频数分布直方图和扇形统计图.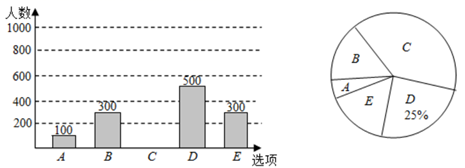
请结合统计图回答下列问题:
(1)、补全频数分布直方图;(2)、扇形统计图中,“会煮饭或会做简单的菜”对应的扇形圆心角是度;(3)、若某市有小学生约 万,请你估计做家务中“洗碗”的总人数.21. 如图,已知,在 , , , .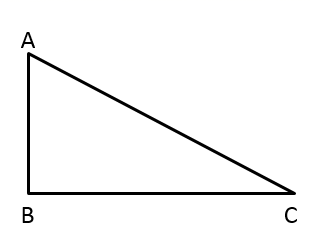
( 1 )在线段 找一点D,使得点D到边 的距离等于 的长(用尺规作图,保留作图痕迹,不要求写作法);
( 2 )在(1)的条件下,求 的长.
22. 某商店销售一款工艺品,每件的成本是30元,为了合理定价投放市场进行试销:据市场调查,销售单价是40元时,每天的销售量是80件,而销售单价每提高1元,每天就少售出2件,但要求销售单价不得超过55元.(1)、若销售单价为每件45元,求每天的销售利润;(2)、要使每天销售这种工艺品盈利1200元,那么每件工艺品售价应为多少元?23. 如图,将一个直角三角形形状的楔子( )从木桩的底端点P沿水平方向打入木桩底下,可以使木桩向上运动.如果楔子底面的斜角为 ,其高度 为 厘米,楔子沿水平方向前进一段距离(如箭头所示),留在外面的楔子长度 为 厘米.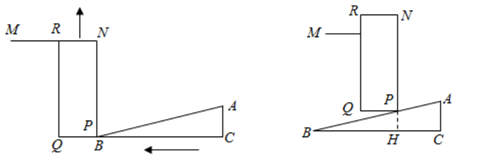 (1)、求 的长;(2)、木桩上升了多少厘米?( , , ,结果精确到 厘米)24. 给出① 平分 ;② 是 的切线,从①或②中选择一个填在下面的文字“且”后面的空格上,再将剩余的一项作为结论填在“则”后面的空格上,构成一个命题.并证明你所构造的命题是真命题.
(1)、求 的长;(2)、木桩上升了多少厘米?( , , ,结果精确到 厘米)24. 给出① 平分 ;② 是 的切线,从①或②中选择一个填在下面的文字“且”后面的空格上,再将剩余的一项作为结论填在“则”后面的空格上,构成一个命题.并证明你所构造的命题是真命题.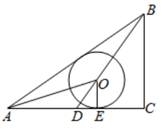 (1)、如图, 中, , 是中线,O在边 上,⊙O与 相切于点E;且 , 则;(2)、根据(1)中的真命题,当 , 时,求⊙O的半径.25. 如图,已知 中, , ,点D为边 上一动点,四边形 是正方形,连接 ,正方形对角线 交 于点F.
(1)、如图, 中, , 是中线,O在边 上,⊙O与 相切于点E;且 , 则;(2)、根据(1)中的真命题,当 , 时,求⊙O的半径.25. 如图,已知 中, , ,点D为边 上一动点,四边形 是正方形,连接 ,正方形对角线 交 于点F.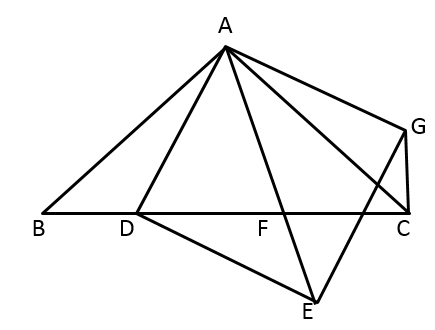 (1)、求证: ;(2)、若 ,求 的值;(3)、若 ,求 的值.26. 如图,在平面直角坐标系xOy中,抛物线y=ax2+(2a﹣ma)x﹣2am(a<0)与x轴分别交于点A、C,顶点坐标为D.
(1)、求证: ;(2)、若 ,求 的值;(3)、若 ,求 的值.26. 如图,在平面直角坐标系xOy中,抛物线y=ax2+(2a﹣ma)x﹣2am(a<0)与x轴分别交于点A、C,顶点坐标为D.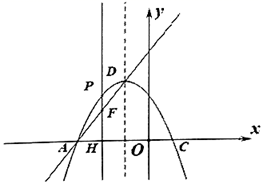 (1)、当a=﹣1,m=1时.
(1)、当a=﹣1,m=1时.①求点D的坐标;
②若F为线段AD上一动点,过点F作FH⊥x轴,垂足为H,交抛物线于点P,当PH+OH的值最大时,求点F的坐标.
(2)、当m= 时,若另一个抛物线y=ax2﹣(6a+ma)x+6am的顶点为E.试判断直线AD是否经过点E?请说明理由.