湖北省武汉市江夏区2021届九年级下学期数学3月月考试卷
试卷更新日期:2021-04-16 类型:月考试卷
一、单选题
-
1. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件是必然事件的是( )A、打开电视机,正在播放《中国好声音》 B、上学路上经过十字路口遇上红灯 C、掷一枚均匀的硬币,正面朝上 D、从1、2、3、4、5这五个数中任取一个数,取到的数一定大于03. 若 是一元二次方程 的两个根,则 的值是( )A、2 B、-2 C、3 D、-34. 点 关于原点对称的点的坐标为( )A、(-2,-3) B、(-2,3) C、(3,2) D、(-3,-2)5. 抛物线 的顶点坐标为( )A、(3,-5) B、(-3,5) C、(-3,-5) D、(3,5)6. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.若一次性摸出两个,则一次性取出的两个小球标号的和不小于4的概率是( )A、 B、 C、 D、7.
2. 下列事件是必然事件的是( )A、打开电视机,正在播放《中国好声音》 B、上学路上经过十字路口遇上红灯 C、掷一枚均匀的硬币,正面朝上 D、从1、2、3、4、5这五个数中任取一个数,取到的数一定大于03. 若 是一元二次方程 的两个根,则 的值是( )A、2 B、-2 C、3 D、-34. 点 关于原点对称的点的坐标为( )A、(-2,-3) B、(-2,3) C、(3,2) D、(-3,-2)5. 抛物线 的顶点坐标为( )A、(3,-5) B、(-3,5) C、(-3,-5) D、(3,5)6. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.若一次性摸出两个,则一次性取出的两个小球标号的和不小于4的概率是( )A、 B、 C、 D、7.如图,为估算学校的旗杆的高度,身高1.6米的小红同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m,BC=8m,则旗杆的高度是( ).
 A、6.4m B、7m C、8m D、9m8. 如图,在 中, , 是高,若 ,则 的值为( )
A、6.4m B、7m C、8m D、9m8. 如图,在 中, , 是高,若 ,则 的值为( ) A、 B、 C、2 D、9. 如图,在△ABC中,AB=AC , BC=6,E为AC边上的点且AE=2EC , 点D在BC边上且满足BD=DE , 设BD=y , S△ABC=x , 则y与x的函数关系式为( )
A、 B、 C、2 D、9. 如图,在△ABC中,AB=AC , BC=6,E为AC边上的点且AE=2EC , 点D在BC边上且满足BD=DE , 设BD=y , S△ABC=x , 则y与x的函数关系式为( )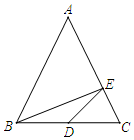 A、y= x2+ B、y= x2+ C、y= x2+2 D、y= x2+210. 如图,直线 交y轴于点A,交双曲线 于点B,将直线 向下平移4个单位长度后与y轴交于点C,交双曲线 于点D,若 ,则n的值( )
A、y= x2+ B、y= x2+ C、y= x2+2 D、y= x2+210. 如图,直线 交y轴于点A,交双曲线 于点B,将直线 向下平移4个单位长度后与y轴交于点C,交双曲线 于点D,若 ,则n的值( )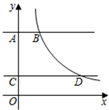 A、4 B、6 C、2 D、5
A、4 B、6 C、2 D、5二、填空题
-
11. 计算:= .
12. 若反比例函数y= 的图象位于一、三象限内,则k的取值范围是 .13. 某药品经过两次降价,每盒零售价由105元降到88元,已知两次降价的百分率相同,设每次降价的百分率为x,根据题意可列方程为.14. 如图,平行于 的直线 把 分成面积相等的两部分,则 . 15. 二次函数 的部分图象如图所示.对称轴为 ,图象过点A,且 ,以下结论:① ;② ;③关于x不等式 的解集: ;④ ;⑤若点 , 在此函数图象上,则 .其中正确的结论是.
15. 二次函数 的部分图象如图所示.对称轴为 ,图象过点A,且 ,以下结论:① ;② ;③关于x不等式 的解集: ;④ ;⑤若点 , 在此函数图象上,则 .其中正确的结论是. 16. 如图, 是 的直径, ,C为 的三等分点(更靠近A点),点P是 上一个动点,取弦 的中点D,则线段 的最大值为.
16. 如图, 是 的直径, ,C为 的三等分点(更靠近A点),点P是 上一个动点,取弦 的中点D,则线段 的最大值为.
三、解答题
-
17. 解方程:18. 如图,一次函数 的图象与反比例函数 的图象交于 、 两点.
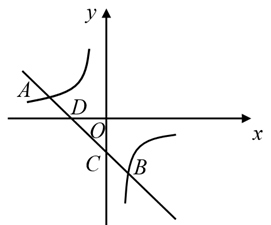 (1)、求反比例函数和一次函数解析式.(2)、结合图象直接写出不等式 的解集.19. 如图,已知 ,求证: .
(1)、求反比例函数和一次函数解析式.(2)、结合图象直接写出不等式 的解集.19. 如图,已知 ,求证: .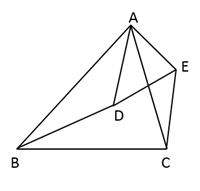 20. 如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点. 的顶点在格点上,仅用无刻度尺的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
20. 如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点. 的顶点在格点上,仅用无刻度尺的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题: (1)、在图1中,过点B作 边上的高 (H为垂足).(2)、在图2中,
(1)、在图1中,过点B作 边上的高 (H为垂足).(2)、在图2中,①在 边上找一点D,使 平分 .
② 边上找一点E,使 .
21. 如图, 为 的切线,A为切点,点B在 上,且 ,连 并延长交 的延长线于点C,交 于点D. (1)、求证: 为 的切线;(2)、连接 、 交于点E.若 , ,求 的值.22. 某水果连锁店销售热带水果,其进价为20元/千克,销售一段时间后发现:该水果的日销售y(千克)与售价x(元/千克)的函数图象关系 ,设日销售利润为w元.(1)、当日销售利润为1600元时,求售价x值;(2)、当售价为多少元/千克时,当日销售利润w最大,最大利润为多少元?(3)、由于某种原因,该水果进价提高了m元/千克 ,物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价的函数关系不变.若日销售最大利润是1280元,请直接写出m的值.23. 如图1, 是 的高, .
(1)、求证: 为 的切线;(2)、连接 、 交于点E.若 , ,求 的值.22. 某水果连锁店销售热带水果,其进价为20元/千克,销售一段时间后发现:该水果的日销售y(千克)与售价x(元/千克)的函数图象关系 ,设日销售利润为w元.(1)、当日销售利润为1600元时,求售价x值;(2)、当售价为多少元/千克时,当日销售利润w最大,最大利润为多少元?(3)、由于某种原因,该水果进价提高了m元/千克 ,物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价的函数关系不变.若日销售最大利润是1280元,请直接写出m的值.23. 如图1, 是 的高, .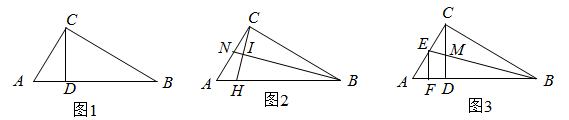 (1)、求证: .(2)、如图2, 是 的中线, 于点I交 于H点,若 ,求 的值.(3)、如图3,M是 的中点, 交 于E, 于F.若 , ,直接写出 的值.24. 如图,已知抛物线经y=ax2+bx﹣3过A(1,0),B(3,0),C三点.
(1)、求证: .(2)、如图2, 是 的中线, 于点I交 于H点,若 ,求 的值.(3)、如图3,M是 的中点, 交 于E, 于F.若 , ,直接写出 的值.24. 如图,已知抛物线经y=ax2+bx﹣3过A(1,0),B(3,0),C三点. (1)、求抛物线解析式;(2)、如图1,点P是BC上方抛物线上一点,作PQ⊥x轴交BC于Q点.请问是否存在点P使得△BPQ为等腰三角形?若存在,请直接写出P点坐标;若不存在,请说明理由;(3)、如图2,连接AC,点D是线段AB上一点,作DE∥BC交AC于E点,连接BE,若△BDE∽△CEB,求D点坐标.
(1)、求抛物线解析式;(2)、如图1,点P是BC上方抛物线上一点,作PQ⊥x轴交BC于Q点.请问是否存在点P使得△BPQ为等腰三角形?若存在,请直接写出P点坐标;若不存在,请说明理由;(3)、如图2,连接AC,点D是线段AB上一点,作DE∥BC交AC于E点,连接BE,若△BDE∽△CEB,求D点坐标.