河南省沁阳市2021届九年级下学期数学第二次月考试卷
试卷更新日期:2021-04-16 类型:月考试卷
一、单选题
-
1. 在下列函数中,y是x的反比例函数的是( )A、y=x-1 B、y= C、y=-2x-1 D、 =22. 如图所示的几何体的左视图是( )
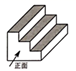 A、
A、 B、
B、 C、
C、 D、
D、 3. 若正比例函数y=﹣2x与反比例函数y=图象的一个交点坐标为(﹣1,2),则另一个交点的坐标为( )A、(2,﹣1) B、(1,﹣2) C、(﹣2,﹣1) D、(﹣2,1)4. 如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
3. 若正比例函数y=﹣2x与反比例函数y=图象的一个交点坐标为(﹣1,2),则另一个交点的坐标为( )A、(2,﹣1) B、(1,﹣2) C、(﹣2,﹣1) D、(﹣2,1)4. 如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( ) A、
A、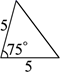 B、
B、 C、
C、 D、
D、 5. 若规定 ,则sin15°=( )A、 B、 C、 D、6. 如图1,在Rt△ABC中,∠B=90°,∠ACB=45°,延长BC到D,使CD=AC,则tan22.5°=( )
5. 若规定 ,则sin15°=( )A、 B、 C、 D、6. 如图1,在Rt△ABC中,∠B=90°,∠ACB=45°,延长BC到D,使CD=AC,则tan22.5°=( )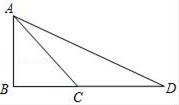 A、 B、 C、 D、7. 如图,一次函数 和反比例函数 的图象相交于 , 两点,则使 成立的 取值范围是( )
A、 B、 C、 D、7. 如图,一次函数 和反比例函数 的图象相交于 , 两点,则使 成立的 取值范围是( )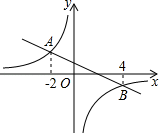 A、 或 B、 或 C、 或 D、 或8. 一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为( )
A、 或 B、 或 C、 或 D、 或8. 一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为( )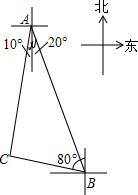 A、 海里/时 B、30海里/时 C、 海里/时 D、 海里/时9. 如图,四边形ABCD是矩形,点E、F是矩形ABCD外两点,AE⊥CF于H,AD=3,DC=4,DE= ,∠EDF=90°,则DF的长是( )
A、 海里/时 B、30海里/时 C、 海里/时 D、 海里/时9. 如图,四边形ABCD是矩形,点E、F是矩形ABCD外两点,AE⊥CF于H,AD=3,DC=4,DE= ,∠EDF=90°,则DF的长是( ) A、 B、 C、 D、10. 在四边形 ABCD 中,∠B=90°,AC=4,AB∥CD,DH 垂直平分AC,点 H 为垂足,设 AB=x,AD=y,则y 关于x 的函数关系用图象大致可以表示为 ( )
A、 B、 C、 D、10. 在四边形 ABCD 中,∠B=90°,AC=4,AB∥CD,DH 垂直平分AC,点 H 为垂足,设 AB=x,AD=y,则y 关于x 的函数关系用图象大致可以表示为 ( )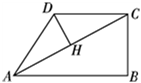 A、
A、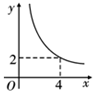 B、
B、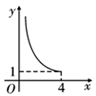 C、
C、 D、
D、
二、填空题
-
11. 如图,在△ABC中,DE∥BC,AD=2BD,则 =.
 12. 下图是由若干个相同的小正方体组合而成的一个几何体的三视图,则组成这个几何体的小正方体个数是.
12. 下图是由若干个相同的小正方体组合而成的一个几何体的三视图,则组成这个几何体的小正方体个数是. 13. 若点A(﹣1,y1)、B(1,y2)、C(3,y3)在反比例函数 的图象上,则y1、y2、y3的大小关系是.14. 如图所示,矩形ABCD的顶点D在反比例函数 (x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,△BCE的面积是6,则k=.
13. 若点A(﹣1,y1)、B(1,y2)、C(3,y3)在反比例函数 的图象上,则y1、y2、y3的大小关系是.14. 如图所示,矩形ABCD的顶点D在反比例函数 (x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,△BCE的面积是6,则k=.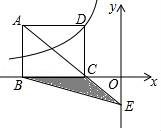
三、解答题
-
15. 计算:16. 如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(﹣2,3),B(﹣3,2),C(﹣1,1).
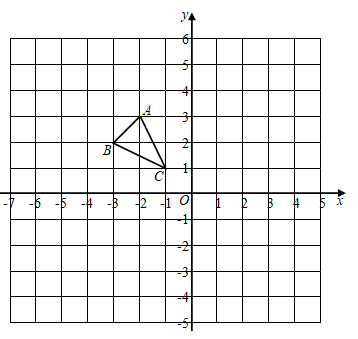 (1)、以坐标原点O为位似中心,2为位似比.将△ABC放大,得到△A´B´C´.请在平面直角坐标系中画出△A´B´C´;(2)、求出△A´B´C´的面积.17. 如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)、以坐标原点O为位似中心,2为位似比.将△ABC放大,得到△A´B´C´.请在平面直角坐标系中画出△A´B´C´;(2)、求出△A´B´C´的面积.17. 如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.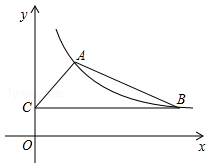 (1)、求该反比例函数的解析式;(2)、若△ABC的面积为6,求直线AB的表达式.18. 如图,点C在△ADE的边DE上,AD与BC相交于点F,∠1=∠2, .
(1)、求该反比例函数的解析式;(2)、若△ABC的面积为6,求直线AB的表达式.18. 如图,点C在△ADE的边DE上,AD与BC相交于点F,∠1=∠2, .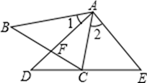 (1)、试说明:△ABC ∽△ADE;(2)、试说明:AF•DF=BF•CF.19. 如图,线段 表示信号塔, 表示一斜坡, .且点 三点在同一水平线上,点 在同一平面内,斜坡 的坡比为 米.某人站在坡顶D处测得塔顶A点的仰角为37°,站在坡底C处测得塔顶A点的仰角为48°(人的身高忽略不计),求信号塔的高度 (结果精确到1米).(参考数据: , ).
(1)、试说明:△ABC ∽△ADE;(2)、试说明:AF•DF=BF•CF.19. 如图,线段 表示信号塔, 表示一斜坡, .且点 三点在同一水平线上,点 在同一平面内,斜坡 的坡比为 米.某人站在坡顶D处测得塔顶A点的仰角为37°,站在坡底C处测得塔顶A点的仰角为48°(人的身高忽略不计),求信号塔的高度 (结果精确到1米).(参考数据: , ).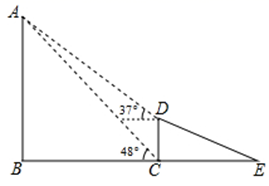 20. 如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
20. 如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.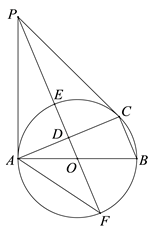
 (1)、求证:PA是⊙O的切线;(2)、证明: ;(3)、若BC=8,tan∠AFP= ,求DE的长.
(1)、求证:PA是⊙O的切线;(2)、证明: ;(3)、若BC=8,tan∠AFP= ,求DE的长.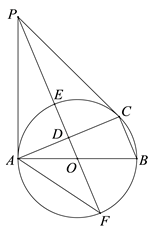 21.
21.
如图1,在 中, ,点D为 边上的动点, 交 于点E.
(1)、问题发现:如图2,当 时, ; 与 所在直线相交所成的锐角等于.(2)、类比探究:当 时,把 绕点A逆时针旋转到如图3的位置时,请求出 的值以及 与 所在直线相交所成的锐角.22. 如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.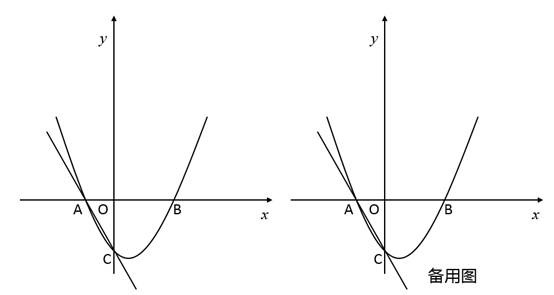 (1)、直接写出二次函数的解析式;(2)、点P在x轴正半轴上,且PA=PC,求OP的长;(3)、点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.若M在y轴右侧,且△CHM∽△AOC,求点M的坐标.
(1)、直接写出二次函数的解析式;(2)、点P在x轴正半轴上,且PA=PC,求OP的长;(3)、点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.若M在y轴右侧,且△CHM∽△AOC,求点M的坐标.