初中数学浙教版2020-2021学年九年级下学期数学期中模拟试卷(1)
试卷更新日期:2021-04-16 类型:期中考试
一、单选题
-
1. 如果一个数的倒数是-3,那么这个数的绝对值是( ).A、 B、- C、3 D、-32. 姑婆山景区是一个环境优美,景色宜人的森林景区,湖南中南林学院的教授曾对姑婆山景区的负氧离子进行过测量,经测量,姑婆山景区达到每立方厘米含负氧离子65558个,可将65558用科学记数法表示为( ).A、6.5558×105 B、6.5558×104 C、65.558×103 D、0.65558×1063. 如图, 是一个中心对称图形的一部分,O点是对称中心,点A和点B是一对对应点, ,那么将这个图形补成一个完整的图形是( )
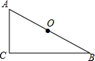 A、矩形 B、菱形 C、正方形 D、梯形4. 如图,在一张长方形纸片上画一条线段AB,将右侧部分纸片四边形ABCD沿线段AB翻折至四边形ABC'D',若∠ABC=58°,则∠1=( )
A、矩形 B、菱形 C、正方形 D、梯形4. 如图,在一张长方形纸片上画一条线段AB,将右侧部分纸片四边形ABCD沿线段AB翻折至四边形ABC'D',若∠ABC=58°,则∠1=( )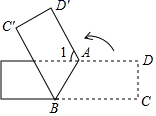 A、60° B、64° C、42° D、52°5. 某同学将自己7次体育测试成绩(单位:分)绘制成折线统计图,则该同学7次测试成绩的众数和中位数分别是( )
A、60° B、64° C、42° D、52°5. 某同学将自己7次体育测试成绩(单位:分)绘制成折线统计图,则该同学7次测试成绩的众数和中位数分别是( )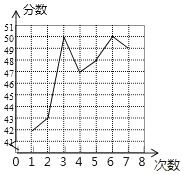 A、50和48 B、50和47 C、48和48 D、48和436. 小颖将一枚质地均匀的硬币连续掷了三次,你认为三次都是正面朝上的概率是( )A、
A、50和48 B、50和47 C、48和48 D、48和436. 小颖将一枚质地均匀的硬币连续掷了三次,你认为三次都是正面朝上的概率是( )A、 B、
C、
D、
7. 如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于( )
B、
C、
D、
7. 如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于( )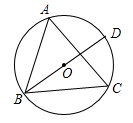 A、33° B、57° C、67° D、66°8. 关于x的一元二次方程x2﹣(k+2)x+2k=0的根的情况是( )A、有两个不相等的实数根 B、总有实数根 C、有两个相等的实数根 D、没有实数根9. 如图,已知 , , 于点C, 于点G,若 ,则 长度是( )
A、33° B、57° C、67° D、66°8. 关于x的一元二次方程x2﹣(k+2)x+2k=0的根的情况是( )A、有两个不相等的实数根 B、总有实数根 C、有两个相等的实数根 D、没有实数根9. 如图,已知 , , 于点C, 于点G,若 ,则 长度是( )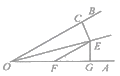 A、3 B、4 C、5 D、610. 如图,若点P为函数 图象上的一动点, 表示点P到原点O的距离,则下列图象中,能表示 与点P的横坐标 的函数关系的图象大致是( )
A、3 B、4 C、5 D、610. 如图,若点P为函数 图象上的一动点, 表示点P到原点O的距离,则下列图象中,能表示 与点P的横坐标 的函数关系的图象大致是( )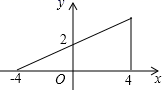 A、
A、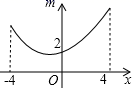 B、
B、 C、
C、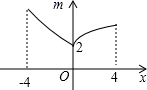 D、
D、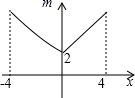
二、填空题
-
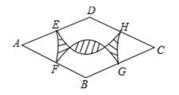
11. 分解因式:x3﹣25x=.12. 如图13,在边长为6的菱形ABCD中,分别以各顶点为圆心,以边长的一半为半径,在菱形内作四条圆弧,则图中阴影部分的周长是。(结果保留π)
 13. 若a、b是有理数,定义新运算△:a△b=2ab−1,例如(−3)△4=2×(−3)×4−1=−25,那么[3△(−2)]△1=.14. 如图,点E、F、G分别在菱形ABCD的边AB,BC,AD上,AE= AB,CF= CB,AG= AD.已知△EFG的面积等于6,则菱形ABCD的面积等于 .
13. 若a、b是有理数,定义新运算△:a△b=2ab−1,例如(−3)△4=2×(−3)×4−1=−25,那么[3△(−2)]△1=.14. 如图,点E、F、G分别在菱形ABCD的边AB,BC,AD上,AE= AB,CF= CB,AG= AD.已知△EFG的面积等于6,则菱形ABCD的面积等于 .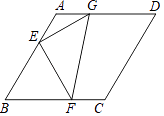 15. 如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE= ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为.
15. 如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE= ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为.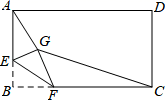 16. 如图,已知线段 ,P是直线 上一动点,点M,N分别为 , 的中点,对下列各值:①线段 的长;② 的周长;③ 的面积;④直线 , 之间的距离;⑤ 的大小.其中不会随点P的移动而改变的是.(填序号)
16. 如图,已知线段 ,P是直线 上一动点,点M,N分别为 , 的中点,对下列各值:①线段 的长;② 的周长;③ 的面积;④直线 , 之间的距离;⑤ 的大小.其中不会随点P的移动而改变的是.(填序号)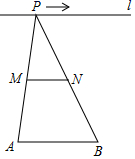
三、计算题
-
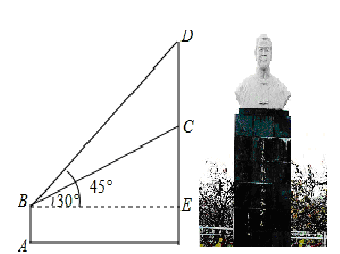
17. 已知 ,且 ,求 的值.18. 解不等式组 ,并求它的所有整数解的和.19. 如图,2019年阳信梨花会期间,部分同学利用周末时间参观各景点,来到朱万祥雕塑前,小明同学站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据: )
 20. 某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机抽取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:
20. 某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机抽取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下: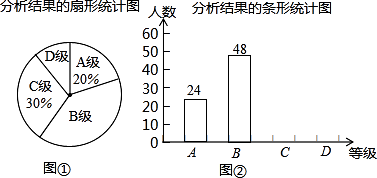
根据上述信息完成下列问题:
(1)、求本次调查共抽取了多少份书法作品?
(2)、请在图②中把条形统计图补充完整;(3)、已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
21. 疫情期间,甲厂欲购买某种无纺布生产口罩,A、B两家无纺布公司各自给出了该种无纺布的销售方案.A公司方案:无纺布的价格均为每吨1.95万元 ;
B公司方案:无纺布不超过30吨时,每吨收费2万元;超过30吨时,超过的部分每吨收费1.9万元.
设甲厂在同一公司一次购买无纺布的数量为x吨(x>0).
(Ⅰ)根据题意,填写下表:
一次购买数量(吨)
10
20
35
…
A公司花费(万元)
39
…
B公司花费(万元)
40
…
(Ⅱ)设在A公司花费 万元,在B公司花费 万元,分别求 、 关于x的函数解析式;
(Ⅲ)如果甲厂所需购买的无纺布是50吨,试通过计算说明选择哪家公司费用较少.
22. 如图,一次函数 的图象分别交 轴、 轴于 , 两点,交反比例函数 图象于 , 两点. (1)、求直线 的表达式;(2)、点 是线段 上一点,若 ,求 点的坐标.23. 如图
(1)、求直线 的表达式;(2)、点 是线段 上一点,若 ,求 点的坐标.23. 如图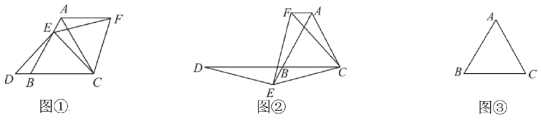 (1)、【问题提出】如图 ,已知 是等边三角形,点E在线段AB上,点D在直线BC上,且
(1)、【问题提出】如图 ,已知 是等边三角形,点E在线段AB上,点D在直线BC上,且 ,将 绕点C顺时针旋转 至 ,连接 试证明: .
(2)、如图 ,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系 请说明理由(3)、如果点E在线段BA的延长线上,其他条件不变,请在图 的基础上将图形补充完整 并写出AB,DB,AF之间的数量关系,不必说明理由24. 在 中, , , .
,将 绕点C顺时针旋转 至 ,连接 试证明: .
(2)、如图 ,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系 请说明理由(3)、如果点E在线段BA的延长线上,其他条件不变,请在图 的基础上将图形补充完整 并写出AB,DB,AF之间的数量关系,不必说明理由24. 在 中, , , .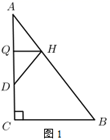
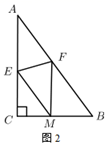
 (1)、如图1,折叠 使点 落在 边上的点D处,折痕交 、 分别于 、 ,若 ,则HQ= .(2)、如图2,折叠 使点 落在 边上的点 处,折痕交 、 分别于 、 .若 ,求证:四边形 是菱形.(3)、如图3,在(1)(2)的条件下,线段 上是否存在点 ,使得 和 相似?若存在,求出 的长;若不存在,请说明理由.
(1)、如图1,折叠 使点 落在 边上的点D处,折痕交 、 分别于 、 ,若 ,则HQ= .(2)、如图2,折叠 使点 落在 边上的点 处,折痕交 、 分别于 、 .若 ,求证:四边形 是菱形.(3)、如图3,在(1)(2)的条件下,线段 上是否存在点 ,使得 和 相似?若存在,求出 的长;若不存在,请说明理由.