2020-2021学年北师大版数学六年级下册期中专项复习:01圆柱
试卷更新日期:2021-04-15 类型:复习试卷
一、选择题
-
1. 下面( )是圆柱的展开图。A、
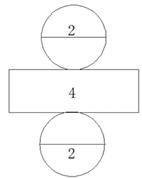 B、
B、 C、
C、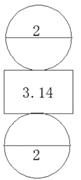 D、
D、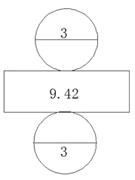 2. 一个圆柱纸筒,底面半径是1厘米,沿侧面高展开后的平面图是正方形,这个纸筒高是( )厘米。A、3.14 B、6.28 C、9.42 D、1.573. 用—块长12.56厘米、宽8厘米的长方形铁皮,配上下面( )圆形铁皮正好可以做成一个无盖的圆柱形容器。A、r=1厘米 B、r=2厘米 C、r=4厘米 D、r=5厘米4. 将圆柱的侧面展开,不可能得到的是( )A、平行四边形 B、长方形 C、正方形 D、扇形5. 一个圆柱侧面展开后是一个边长15.7厘米的正方形。这个圆柱的底面面积是( )平方厘米。A、15.7 B、19.625 C、78.56. 学校学术报告厅内有5根相同的圆柱形立柱,柱子的高是4米,底面的周长是π米。给这5根柱子刷油漆,每平方米用油漆0.4千克,一共需要油漆( )千克。A、2π B、π C、4π D、8π7. 如图,把底面直径4厘米的圆柱切成若干等份,拼成一个近似的长方体,这个长方体的表面积比原来增加40平方厘米。那么长方体的高是( )厘米。
2. 一个圆柱纸筒,底面半径是1厘米,沿侧面高展开后的平面图是正方形,这个纸筒高是( )厘米。A、3.14 B、6.28 C、9.42 D、1.573. 用—块长12.56厘米、宽8厘米的长方形铁皮,配上下面( )圆形铁皮正好可以做成一个无盖的圆柱形容器。A、r=1厘米 B、r=2厘米 C、r=4厘米 D、r=5厘米4. 将圆柱的侧面展开,不可能得到的是( )A、平行四边形 B、长方形 C、正方形 D、扇形5. 一个圆柱侧面展开后是一个边长15.7厘米的正方形。这个圆柱的底面面积是( )平方厘米。A、15.7 B、19.625 C、78.56. 学校学术报告厅内有5根相同的圆柱形立柱,柱子的高是4米,底面的周长是π米。给这5根柱子刷油漆,每平方米用油漆0.4千克,一共需要油漆( )千克。A、2π B、π C、4π D、8π7. 如图,把底面直径4厘米的圆柱切成若干等份,拼成一个近似的长方体,这个长方体的表面积比原来增加40平方厘米。那么长方体的高是( )厘米。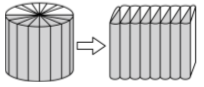 A、4 B、8 C、10 D、208. 圆柱的底面半径扩大2倍,高不变。它的体积扩大( )倍。A、2 B、4 C、8 D、169. 下面图形中,用“底面积×高”不能直接计算出体积的是( )。A、
A、4 B、8 C、10 D、208. 圆柱的底面半径扩大2倍,高不变。它的体积扩大( )倍。A、2 B、4 C、8 D、169. 下面图形中,用“底面积×高”不能直接计算出体积的是( )。A、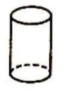 B、
B、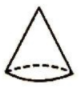 C、
C、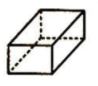 D、
D、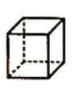 10. 如图,把圆柱体切拼成长方体,切拼后图形的体积和表面积( )。
10. 如图,把圆柱体切拼成长方体,切拼后图形的体积和表面积( )。 A、都不变 B、体积不变表面积变大 C、体积不变表面积变小 D、都变大11. 把一个长8分米、宽6分米、高7分米的长方体木块,削成一个体积最大的圆柱。求这个圆柱体积的算式是( )。A、3.14×( )²×7 B、3.14×( )²×6 C、3.14×( )²×7 D、3.14×( )²×8
A、都不变 B、体积不变表面积变大 C、体积不变表面积变小 D、都变大11. 把一个长8分米、宽6分米、高7分米的长方体木块,削成一个体积最大的圆柱。求这个圆柱体积的算式是( )。A、3.14×( )²×7 B、3.14×( )²×6 C、3.14×( )²×7 D、3.14×( )²×8二、判断题
-
12. 一个圆柱的侧面展开是正方形,则这个圆柱的高与底面直径相等。( )13. 圆柱和圆锥的高都有无数条。( )14. 圆柱的侧面展开后一定是长方形或正方形。( )15. 一个圆柱体的底面直径是d,高也是d,它的侧面展开图形是正方形。( )16. 把一个侧面积是157平方厘米的圆柱,沿底面半径平均分成若干等份切开,拼成一个近似的长方体,表面积增加25平方厘米。( )17. 用一张长方形的纸围成一个圆柱(不能有重合部分),有两种围法,这两种围法所得到圆柱的侧面积相等。( )18. 圆柱的底面半径扩大到原来的3倍,高不变,它的侧面积和底面积都扩大到原来的3倍。( )
三、填空题
-
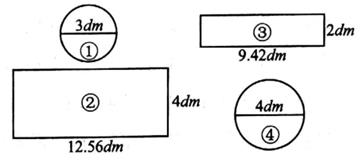
19. 制作一个无盖的圆柱形水桶,有以下四种型号的铁皮可供选择(不考虑损耗)。要恰好做成水桶,你选择的材料是号和号。
 20. 圆柱的侧面展开后的图形是 , 圆锥的侧面展开后的图形是 .21. 把一个底面直径为3厘米、高是5厘米的圆柱体沿直径切割成两个半圆柱,表面积增加了。22. 做一个底面直径为20厘米、长为90厘米的烟囱,至少需要平方厘米的铁皮。23. 把下图所示的长方形铁皮卷成一个高2分米的圆柱形铁桶,铁桶的底面直径大约是分米,加上底面后,铁桶的表面积约是平方分米,容积大约是升。(铁皮的厚度忽略不计)
20. 圆柱的侧面展开后的图形是 , 圆锥的侧面展开后的图形是 .21. 把一个底面直径为3厘米、高是5厘米的圆柱体沿直径切割成两个半圆柱,表面积增加了。22. 做一个底面直径为20厘米、长为90厘米的烟囱,至少需要平方厘米的铁皮。23. 把下图所示的长方形铁皮卷成一个高2分米的圆柱形铁桶,铁桶的底面直径大约是分米,加上底面后,铁桶的表面积约是平方分米,容积大约是升。(铁皮的厚度忽略不计) 24. 一个圆柱底面直径是6厘米,高4厘米,侧面积是平方厘米,体积是立方厘米。与这个圆柱等底等高的圆锥体积是立方厘米。25. 把一个长12分米的圆柱体木料,锯成3个小圆柱体,表面积增加了32平万分米,这根圆柱体木料的体积是立方分米。26. 一个圆柱形罐头盒的侧面贴着商标纸,圆柱底面半径是5cm,高是20cm。如果这张商标纸展开后是一个长方形,则它的长是cm,宽是cm,面积是cm2.27. 把一根长16米的方木锯成相等的5段,表面积增加了4平方米,这根方木的体积是立方米。28. 一个体积为200立方分米的正方体,削成一个最大的圆柱,这个圆柱的体积是立方分米。29. 一个圆柱的侧面展开后,正好得到1个边长25.12厘米的正方形,这个圆柱的体积是立方厘米。30. 有一根半径是2厘米,高6厘米的圆柱形钢材,加工成与它等底等高的圆锥,要切去立方厘米钢材。31. 如图所示,把一个高为10厘米的圆柱切成若干份,拼成一个近似的长方体。如果这个长方体的底面积是50平方厘米,那么,圆柱体积是立方厘米。
24. 一个圆柱底面直径是6厘米,高4厘米,侧面积是平方厘米,体积是立方厘米。与这个圆柱等底等高的圆锥体积是立方厘米。25. 把一个长12分米的圆柱体木料,锯成3个小圆柱体,表面积增加了32平万分米,这根圆柱体木料的体积是立方分米。26. 一个圆柱形罐头盒的侧面贴着商标纸,圆柱底面半径是5cm,高是20cm。如果这张商标纸展开后是一个长方形,则它的长是cm,宽是cm,面积是cm2.27. 把一根长16米的方木锯成相等的5段,表面积增加了4平方米,这根方木的体积是立方米。28. 一个体积为200立方分米的正方体,削成一个最大的圆柱,这个圆柱的体积是立方分米。29. 一个圆柱的侧面展开后,正好得到1个边长25.12厘米的正方形,这个圆柱的体积是立方厘米。30. 有一根半径是2厘米,高6厘米的圆柱形钢材,加工成与它等底等高的圆锥,要切去立方厘米钢材。31. 如图所示,把一个高为10厘米的圆柱切成若干份,拼成一个近似的长方体。如果这个长方体的底面积是50平方厘米,那么,圆柱体积是立方厘米。 32. “转化”是一种重要的数学思想方法,在学习中经常用到。例如,在学习小数乘法时,先把它转化为整数乘法,然后探究它的计算方法;在探充平行四边形面积公式时,先把它转化为长方形,然后推导出计算公式。请你再举一个学习数学知识时应用“转化”的例子:。33. 一个圆柱与一个圆锥的底面积相等,体积的比是6:1.如果圆锥的高是8.4厘米,那么圆柱的高是厘米.如果圆柱的高是8.4厘米,那么圆锥的高是厘米.34. 将好一个棱长为8厘米的正方体木块削成一个最大的圆柱,圆柱体积是立方厘米。35. 一瓶汽水的净含量是1.2L,把这样一瓶汽水倒入底面积20cm2 , 高12cm的圆柱形小杯中,能倒满杯。
32. “转化”是一种重要的数学思想方法,在学习中经常用到。例如,在学习小数乘法时,先把它转化为整数乘法,然后探究它的计算方法;在探充平行四边形面积公式时,先把它转化为长方形,然后推导出计算公式。请你再举一个学习数学知识时应用“转化”的例子:。33. 一个圆柱与一个圆锥的底面积相等,体积的比是6:1.如果圆锥的高是8.4厘米,那么圆柱的高是厘米.如果圆柱的高是8.4厘米,那么圆锥的高是厘米.34. 将好一个棱长为8厘米的正方体木块削成一个最大的圆柱,圆柱体积是立方厘米。35. 一瓶汽水的净含量是1.2L,把这样一瓶汽水倒入底面积20cm2 , 高12cm的圆柱形小杯中,能倒满杯。四、解答题
-
36. 如图,一个圆柱高8cm,如果它的高增加4cm,那么它的表面积就增加50.24cm2。求原来圆柱的体积。
 37. 一个圆柱形纸筒的高是18dm,它的侧面展开后是一个正方形。这个圆柱形纸筒的侧面积是多少平方分米?38. 一根长是2m、横截面直径是40cm的圆柱体木头浮在水面上,小明发现它正好有一半露出水面。这根木头与水接触的面积是多少平方厘米?这根木头露出水面部分的体积是多少立方厘米?
37. 一个圆柱形纸筒的高是18dm,它的侧面展开后是一个正方形。这个圆柱形纸筒的侧面积是多少平方分米?38. 一根长是2m、横截面直径是40cm的圆柱体木头浮在水面上,小明发现它正好有一半露出水面。这根木头与水接触的面积是多少平方厘米?这根木头露出水面部分的体积是多少立方厘米? 39. 用粗细不同的两根圆柱形木料,制作一个简易的木槌(如下图),如果要在木槌表面涂一层油漆,那么涂油漆的面积是多少平方厘米?
39. 用粗细不同的两根圆柱形木料,制作一个简易的木槌(如下图),如果要在木槌表面涂一层油漆,那么涂油漆的面积是多少平方厘米? 40. 一台压路机的前轮是圆柱形的,轮宽2m,直径1m。如果这台压路机在工作时前轮每分钟转10圈,那么它每分钟可压路面多少平方米?
40. 一台压路机的前轮是圆柱形的,轮宽2m,直径1m。如果这台压路机在工作时前轮每分钟转10圈,那么它每分钟可压路面多少平方米? 41. 把底面积相等的一块圆锥形铁块和一块圆柱形铁块先后浸没在长是10cm、宽是8cm的盛有水的长方体容器中,没有水溢出。先放入圆锥形铁块,水面上升了2cm;再放入圆柱形铁块,水面又上升了2cm。(1)、如果圆锥形铁块的高是12cm,那么圆柱形铁块的高是多少?(2)、如果每立方厘米铁块重7.8g,那么这个圆锥形铁块重多少克?42. 用一个底面直径和高都是10cm的圆柱形橡皮泥做手工作品,如果捏一个手工作品要用橡皮泥25cm3 , 那么这块橡皮泥最多能捏多少个这样的手工作品?43. 一瓶老酸奶(如图①),奶瓶深20cm,内直径是8cm,瓶中的酸奶深10cm。把瓶盖拧紧倒置放平,这时酸奶深15cm(如图②)。这个奶瓶最多能装多少毫升酸奶?
41. 把底面积相等的一块圆锥形铁块和一块圆柱形铁块先后浸没在长是10cm、宽是8cm的盛有水的长方体容器中,没有水溢出。先放入圆锥形铁块,水面上升了2cm;再放入圆柱形铁块,水面又上升了2cm。(1)、如果圆锥形铁块的高是12cm,那么圆柱形铁块的高是多少?(2)、如果每立方厘米铁块重7.8g,那么这个圆锥形铁块重多少克?42. 用一个底面直径和高都是10cm的圆柱形橡皮泥做手工作品,如果捏一个手工作品要用橡皮泥25cm3 , 那么这块橡皮泥最多能捏多少个这样的手工作品?43. 一瓶老酸奶(如图①),奶瓶深20cm,内直径是8cm,瓶中的酸奶深10cm。把瓶盖拧紧倒置放平,这时酸奶深15cm(如图②)。这个奶瓶最多能装多少毫升酸奶?
