初中数学北师大版八年级下学期期中考试复习专题：02 垂直平分线、角平分线
试卷更新日期：2021-04-15 类型：复习试卷
一、单选题
-
1. 如图，在△ABC中，∠ACB＝90°，边AB的垂直平分线交AB于点D，交AC于点E，连接BE，CD，若BC＝5，CD＝6.5，则△BCE的周长为（ ）
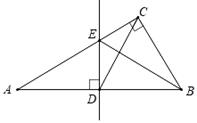A、16.5 B、17 C、18 D、202. 如图，在 中， ， 的垂直平分线DE分别交AB，BC于点D，E，则 的度数为（ ）
A、 B、 C、 D、3. 如图，已知AB=AC，∠A=36°，AB的垂直平分线MD交AC于点D，AB于M，以下结论：①△BCD是等腰三角形；②射线BD是△ACB的角平分线；③△BCD的周长C△BCD=AC+BC；④△ADM≌△BCD．正确的有（ ）
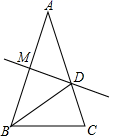A、①②③ B、①② C、①③ D、③④4. 如图，Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，过点D作DF⊥AB，垂足为点F，点E在边AC上，若DE＝DB，则下列结论不正确的是（ ）
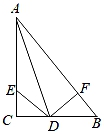A、DC＝DF B、DE＝BF C、AC＝AF D、AB＝AC+CE5. 如图所示，有三条道路围成Rt△ABC，其中BC=1000m，一个人从B处出发沿着BC行走了800m，到达D处，AD恰为∠CAB的平分线，则此时这个人到AB的最短距离为（ ）
A、1000m B、800m C、200m D、1800m二、填空题
-
6. 在 中， ， ， 是斜边 的中垂线，交 于点 ， 的周长为14，则 .7. 如图所示，在△ABC中，∠C = 90°，边AB的垂直平分线分别交AB，AC边于点D，E，连结BE.若AB = 10，BC = 6，则△ACE的周长是 .
8. 如图，在 中， 平分 点 分别是 上的动点.若 则 的最小值是.
三、解答题
-
9. 已知：OB是∠AOC的角平分线，OC是∠AOD的角平分线，∠COD＝40°．分别求∠AOD和∠BOC的度数．
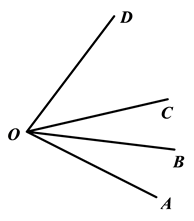10. 如图， ， 表示两个仓库，要在 ， 一侧的河岸边建造一个码头 ，使它到两个仓库的距离相等，码头 应建造在什么位置？
11. 如图，已知等腰三角形 的顶角 .
(1)、在 上作一点 ，使 （要求：尺规作图，保留作图痕迹，不必写作法和证明）.(2)、写出 的度数.四、综合题
