辽宁省盘锦市大洼区2020-2021学年九年级下学期数学开学考试试卷

试卷更新日期：2021-04-14 类型：开学考试

进入出卷网下载

一、单选题

1. 下列图形中，你认为既是中心对称图形又是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. “a是实数，|a|≥0”这一事件是（）

A、必然事件 B、不确定事件 C、不可能事件 D、随机事件

查看试题解析
3. 点 $B (1, - 2)$ 关于原点 $O$ 对称的点 $B_{1}$ 的坐标是（）

A、 $(1,2)$ B、 $(- 1, 0)$ C、 $(- 1, - 2)$ D、 $(- 1, 2)$

查看试题解析
4.
如图，点A是反比例函数y= $\frac{k}{x}$ 的图象上的一点，过点A作AB⊥x轴，垂足为B．点C为y轴上的一点，连接AC，BC．若△ABC的面积为3，则k的值是（　　）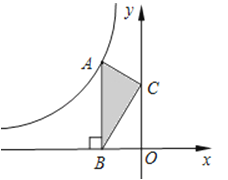

A、3 B、﹣3 C、6 D、﹣6

查看试题解析
5. 如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，若△ADE与四边形DBCE的面积相等，则 $\frac{D E}{B C}$ 等于（）

A、1 B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
6. 反比例函数 $y = \frac{m}{x}$ 的图象如图所示，下列说法正确的是（）

A、常数 $m < - 1$ B、在每个象限内， $y$ 随 $x$ 的增大而增大 C、若 $A (- 1 ， h)$ ， $B (2 ， k)$ 在图象上，则 $h < k$ D、若 $P (x ， y)$ 在图象上，则 $P' (x ， - y)$ 也在图象上

查看试题解析
7. 如图，⊙O是△ABC的内切圆，则点O是△ABC的（）

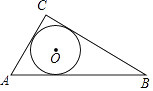A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 30 °$ ， $B C = 4 c m$ ，以点 $C$ 为圆心，以 $2 c m$ 的长为半径作圆，则 $⊙ C$ 与 $A B$ 的位置关系是（）

A、相交 B、相切 C、相离 D、相切或相离

查看试题解析
9. 如图，正方形 $A B C D$ 中， $M$ 是 $B C$ 上一点， $M E ⊥ A M$ ， $M E$ 交 $A D$ 的延长线于点 $E$ ．若 $A B = 12$ ， $B M = 5$ ，则 $D E$ 的长为（）

A、18 B、 $\frac{109}{5}$ C、 $\frac{96}{5}$ D、 $\frac{25}{5}$

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，下列说法① $a > 0$ ；② $b^{2} - 4 a c > 0$ ；③图象关于直线 $x = 1$ 对称；④ $4 a + 2 b + c > 0$ ；⑤当 $x > 1$ 时 $y$ 随 $x$ 的增大而增大，其中正确的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 某市民政部门举行“即开式福利彩票”销售活动，发行彩票10万张（每张彩票2元），在这些彩票中，设置如下奖项：

奖金（元）

10000

5000

1000

500

100

50

数量（个）

1

4

20

40

100

200

如果花2元钱购买1张彩票，那么所得奖金不多于100元的概率是

查看试题解析
12. 方程 $x (x - 1) = 2 (x - 1)$ 的根为．

查看试题解析
13. 如图，正五边形 $A B C D E$ 内接于 $⊙ O$ ，点 $F$ 在弧 $C D$ 上，则 $∠ B F E$ 的度数为

查看试题解析
14. 一药品售价100元，连续两次降价后的价格为81元，则平均每次降价的降价率是 %．

查看试题解析
15. 如图，正六边形内接于⊙O，小明向圆内投掷飞镖一次，则飞镖落在阴影部分的概率是．

查看试题解析
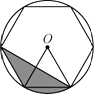16. 已知⊙O的直径AB=2，过点A的两条弦AC= $\sqrt{2}$ ， AD= $\sqrt{3}$ ，则∠CBD=

查看试题解析

三、解答题

17. 如图，在平面直角坐标系中， $△ A O B$ 为直角三角形， $A (- 2 ； 4)$ ， $B (- 2 ， 0)$ ，按要求解答下列问题：

(1)、以原点 $O$ 为位似中心画出 $△ A_{1} O B_{1}$ ，使它与 $△ A O B$ 的相似比为3：2

(2)、将 $△ A_{1} O B_{1}$ 绕点 $O$ 顺时针旋转90°，画出旋转后的 $R t △ A_{2} O B_{2}$

(3)、用点 $A_{1}$ 旋转到点 $A_{2}$ 所经过的路径与 $O A_{1}$ 、 $O A_{2}$ 围成的扇形做成一个圆锥的侧面（接缝忽略不计），求这个圆锥的高．（保留精确值）

查看试题解析
18. 红星粮库需要把晾晒场上的 $1200 t$ 玉米入库封存，

(1)、入库所需的时间 $d$ （单位：天）与入库平均速度 $v$ （单位： $t /$ 天）的函数关系是

(2)、已知粮库有60名职工晾晒，每天最多可入库300t玉米，预计玉米入库最快可在几天内完成？

(3)、60名职工连续工作两天后，天气预报说未来几天会下雨，粮库决定次日把剩下的玉米全部入库，则至少需要增加多少职工？

查看试题解析
19. 如图，甲、乙两个可以自由转动的均匀的转盘，甲转盘被分成4个面积相等的扇形，乙转盘被分成3个面积相等的扇形，每一个扇形都标有相应的数字，同时转动两个转盘，当转盘停止后，设甲转盘中指针所指区域内的数字为 $m$ ，乙转盘中指针所指区域内的数字为 $n$ （若指针指在边界线上时，重转一次，直到指针都指向一个区域为止）．

(1)、请你用画树状图或列表格的方法求出 $| m + n | > 1$ 的概率；

(2)、直接写出点 $(m ， n)$ 落在函数 $y = - \frac{1}{x}$ 图象上的概率

查看试题解析
20. 如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连结AC交⊙O于点F．

(1)、AB与AC的大小有什么关系？请说明理由；

(2)、若AB=8，∠BAC=45°，求：图中阴影部分的面积．

查看试题解析
21. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，点 $D$ 在线段 $A B$ 上，以 $A D$ 为直径的 $⊙ O$ 与 $B C$ 相交于点 $E$ ，与 $A C$ 相交于点 $F$ ， $D E = E F$ ．

(1)、写出图中所有与 $△ A D E$ 相似的三角形；

(2)、求证： $B C$ 是 $⊙ O$ 的切线；

(3)、若 $A C = 3$ ， $B C = 4$ ，求 $⊙ O$ 的半径 $r$ ；

查看试题解析
22. 某地计划对矩形广场进行扩建改造.如图，原广场长50m，宽40m，要求扩充后的矩形广场长与宽的比为3：2.扩充区域的扩建费用每平方米30元，扩建后在原广场和扩充区域都铺设地砖，铺设地砖费用每平方米100元.如果计划总费用642000元，扩充后广场的长和宽应分别是多少米？

查看试题解析
23. 鹏鹏童装店销售某款童装，每件售价为60元，每星期可卖100件，为了促销，该店决定降价销售，经市场调查反应：每降价1元，每星期可多卖10件．已知该款童装每件成本30元，设该款童装每件售价 $x$ 元，每星期的销售量为 $y$ 件．

(1)、每件童装降价元；（用含 $x$ 的式子表示）

(2)、求 $y$ 与 $x$ 之间的函数关系式（不求自变量的取值范围）；

(3)、当每件售价定为多少元时，每星期的销售利润最大，最大利润是多少？

(4)、当每件童装售价定为多少元时，该店一星期可获得3910元的利润？

查看试题解析
24. 在梯形 $A B C D$ 中， $A B // C D$ ， $∠ B C D = 90 °$ ， $B C = D C$ ，对角线 $A C$ 和 $B D$ 相交于点 $O$ ，等腰直角 $△ E C F$ 的直角顶点 $C$ 与梯形的顶点 $C$ 重合，将 $△ E C F$ 绕点 $C$ 旋转

(1)、如图1，当 $△ E C F$ 的一边 $C E$ 落在 $B C$ 边上，另一边 $C F$ 落在 $D C$ 边的延长线上时，求证： $△ B C F ≌ △ D C E$

(2)、继续旋转 $△ E C F$ ，旋转角为 $α$ ，请你在图2中画出图形，并判断（1）中的结论是否成立？若成立加以证明：若不成立，说明理由；

(3)、如图3，继续旋转 $△ E C F$ ，当三角形的一边 $C F$ 与梯形对角线 $A C$ 重合， $E F$ 与 $C D$ 相交于点 $P$ 时，若 $A B = 1$ ， $B C = 2$ ， $O F = \frac{\sqrt{5}}{6}$ ，分别求出线段 $O A$ 、 $O B$ 、 $E P$ 的长．

查看试题解析
25. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + 3$ 经过 $B (- 1 ， 0)$ 、 $C (3 ， 0)$ 两点，

(1)、求抛物线的解析式及顶点 $A$ 的坐标；

(2)、在二次函数的图象位于 $x$ 轴上方的部分有两个动点 $M$ 、 $N$ ，且点 $N$ 在点 $M$ 的左侧，过点 $M$ 、 $N$ 作 $x$ 轴的垂线，分别交 $x$ 轴于点 $H$ 、 $G$ ．
①当四边形 $M N G H$ 为正方形时，求 $M N$ 的长；

②当四边形 $M N G H$ 为矩形时，求矩形 $M N G H$ 周长的最大值

查看试题解析

奖金（元）	10000	5000	1000	500	100	50
数量（个）	1	4	20	40	100	200