初中数学浙教版2020-2021学年八年级下学期数学期中模拟试卷(1)
试卷更新日期:2021-04-14 类型:期中考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 + = B、 - =-1 C、 × = D、 ÷ =3. 如果关于x的一元二次方程(k-1)x2﹣2x+1=0有两个不相等的实数根,那么k的取值范围是( )A、k<2 B、k>2且k≠1 C、k<2且k≠1 D、k>24. 若 , , , 的平均数为4, , , , , 的平均数为6,则 , , , 的平均数为( )A、5 B、4.8 C、5.2 D、85. 一个多边形每一个外角都等于 ,则这个多边形的边数为( )A、12 B、10 C、8 D、66. 用反正法证明命题“如图,如果 , ,那么 ”时,证明的第一个步骤是( )
2. 下列计算正确的是( )A、 + = B、 - =-1 C、 × = D、 ÷ =3. 如果关于x的一元二次方程(k-1)x2﹣2x+1=0有两个不相等的实数根,那么k的取值范围是( )A、k<2 B、k>2且k≠1 C、k<2且k≠1 D、k>24. 若 , , , 的平均数为4, , , , , 的平均数为6,则 , , , 的平均数为( )A、5 B、4.8 C、5.2 D、85. 一个多边形每一个外角都等于 ,则这个多边形的边数为( )A、12 B、10 C、8 D、66. 用反正法证明命题“如图,如果 , ,那么 ”时,证明的第一个步骤是( ) A、假设 不平行于 B、假设 不平行于 C、假设 D、假设 不平行于7. 如图,在 中, , ,点 在 边上,以 , 为边作▱BCDE,则 的度数为
A、假设 不平行于 B、假设 不平行于 C、假设 D、假设 不平行于7. 如图,在 中, , ,点 在 边上,以 , 为边作▱BCDE,则 的度数为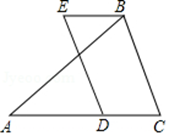 A、 B、 C、 D、8. 下列各组图形中,四个顶点一定在同一圆上的是( )A、矩形,菱形 B、矩形,正方形 C、菱形,正方形 D、平行四边形,菱形9. 如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )
A、 B、 C、 D、8. 下列各组图形中,四个顶点一定在同一圆上的是( )A、矩形,菱形 B、矩形,正方形 C、菱形,正方形 D、平行四边形,菱形9. 如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )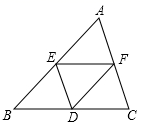 A、20 B、15 C、10 D、510. 如图,在 中, ,以其三边为边向外作正方形,过点 作 于点 ,再过点 作 分别交边 , 于点 , .若 , ,则 的长为
A、20 B、15 C、10 D、510. 如图,在 中, ,以其三边为边向外作正方形,过点 作 于点 ,再过点 作 分别交边 , 于点 , .若 , ,则 的长为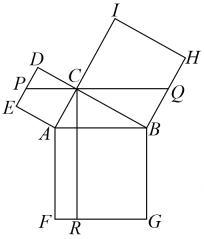 A、14 B、15 C、 D、
A、14 B、15 C、 D、二、填空题
-
11. 要使 有意义,则x的取值范围为.12. 某班7个兴趣小组的人数如下:5,6,6,x,7,8,9,已知这组数据的平均数为7,则这组数据的中位数是.13. 一个正n边形的每一外角都等于60°,则n的值是.14. 某商品原价289元,经过连续两次降价后,售价为256元.设平均每次降价的百分率为x,则x的值为 .15. 如图,在 中, ,D是BC上的任一点, 交AC于点E, 交AB于点F那么四边形AFDE的周长是 .
 16. 如图,点 的坐标为 ,点 在 轴上,把 沿 轴向右平移到 ,若四边形 的面积为9,则点 的坐标为 .
16. 如图,点 的坐标为 ,点 在 轴上,把 沿 轴向右平移到 ,若四边形 的面积为9,则点 的坐标为 .
三、解答题
-
17. 解方程(1)、(2)、(3)、(4)、18. 某中学课外兴趣活动小组准备围建一个矩形的苗圃圆.其中一边靠墙,另外三边用长为 的篱笆围成.已知墙长为 (如图所示),设这个苗圃园垂直于墙的一边 为 ,若苗圃园的面积为 ,求 的长度.
 19. 在平面直角坐标系中,△ABC的位置如图所示,三个顶点的坐标分别为:A(1,2)、B(2,3)、C(3,0).
19. 在平面直角坐标系中,△ABC的位置如图所示,三个顶点的坐标分别为:A(1,2)、B(2,3)、C(3,0).
⑴现将△ABC先向左平移5个单位长度,再向上平移2个单位长度,得到△A1B1C1 , 请在平面直角坐标系中画出△A1B1C1 .
⑵此时平移的距离是多少;
⑶在平面直角坐标系中画出△ABC关于点O成中心对称的△A2B2C2 .
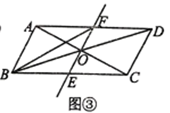
20.如图, 是 的中线, 是线段 上一点(不与点 重合). 交 于点 , ,连结 .
 (1)、如图1,当点 与 重合时,求证:四边形 是平行四边形;(2)、如图2,当点 不与 重合时,(1)中的结论还成立吗?请说明理由.(3)、如图3,延长 交 于点 ,若 ,且 .
(1)、如图1,当点 与 重合时,求证:四边形 是平行四边形;(2)、如图2,当点 不与 重合时,(1)中的结论还成立吗?请说明理由.(3)、如图3,延长 交 于点 ,若 ,且 .①求 的度数;
②当 , 时,求 的长.
21. 如图,平行四边形ABCD中,对角线AC与BD相交于点O,AG⊥BD于G,CH⊥BD于H. (1)、求证:OG=OH;(2)、若∠BAC=90°,∠AOD=120°,请直接写出图中所有长度是OG长度2倍的线段.22. 某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨),并将调查数据进行了如下整理:
(1)、求证:OG=OH;(2)、若∠BAC=90°,∠AOD=120°,请直接写出图中所有长度是OG长度2倍的线段.22. 某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨),并将调查数据进行了如下整理:
分组
划记
频数
2.0<x≤3.5
正正一
11
3.5<x≤5.0

19
5.0<x≤6.5
6.5<x≤8.0
8.0<x≤9.5

2
合计
50
 (1)、把上面的频数分布表和频数分布直方图补充完整;(2)、请你用频数分布直方图计算这50个家庭去年的月均用水量的平均数和中位数(各组的实际数据用该组的组中值表示);若该小区有2000个家庭,请你用频数分布直方图得到的数据估计该小区月均用水总量;(3)、为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量标准应该定为多少?为什么?
(1)、把上面的频数分布表和频数分布直方图补充完整;(2)、请你用频数分布直方图计算这50个家庭去年的月均用水量的平均数和中位数(各组的实际数据用该组的组中值表示);若该小区有2000个家庭,请你用频数分布直方图得到的数据估计该小区月均用水总量;(3)、为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量标准应该定为多少?为什么?