山东省烟台市栖霞市2019-2020学年七年级下学期数学期中试卷

试卷更新日期：2021-04-14 类型：期中考试

进入出卷网下载

一、单选题

1. 方程组 ${\begin{array}{l} x + y = 1 \\ 2 x + y = 5 \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ C、 ${\begin{array}{l} x = 4 \\ y = - 3 \end{array}$ D、 ${\begin{array}{l} x = - 2 \\ y = 3 \end{array}$

查看试题解析
2. 给出下列命题：
⑴三角形的一个外角一定大于它的一个内角.
⑵若一个三角形的三个内角之比为1：3：4，它肯定是直角三角形.
⑶三角形的最小内角不能大于60°.
⑷三角形的一个外角等于和它不相邻的两个内角的和.
其中真命题的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列事件中，必然事件是（　　）

A、抛掷1个均匀的骰子，出现6点向上 B、两直线被第三条直线所截，同位角相等 C、366人中至少有2人的生日相同 D、实数的绝对值是非负数

查看试题解析
4. 由方程组 ${\begin{array}{l} x + m = 4 \\ y - 3 = m \end{array}$ 可得出x与y的关系是（）

A、x+y=1 B、x+y=﹣1 C、x+y=7 D、x+y=﹣7

查看试题解析
5. 如图，下列条件： $① ∠ 1 = ∠ 3 ， ② ∠ 2 + ∠ 4 = 180^{\circ} ， ③ ∠ 4 = ∠ 5 ， ④ ∠ 2 = ∠ 3 ， ⑤ ∠ 6 = ∠ 2 + ∠ 3$ 中能判断直线 $l_{1} ∥ l_{2}$ 的有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
6. 某班四个小组进行辩论比赛，赛前三位同学预测比赛结果如下：
甲说：“第二组得第一，第四组得第三”；
乙说：“第一组得第四，第三组得第二”；
丙说：“第三组得第三，第四组得第一”；
赛后得知，三人各猜对一半，则冠军是（　　）

A、第一组 B、第二组 C、第三组 D、第四组

查看试题解析
7. 下列用消元法解二元一次方程组 ${\begin{array}{l} x - 2 y = - 1...... ① \\ 2 x - 5 y = 1...... ② \end{array}$ 中，错误的是（）

A、由①得： $x = 2 y - 1$ B、由① $\times 2 -$ ②得： $- 9 y = - 3$ C、由① $\times 5 -$ ② $\times 2$ 得： $x = - 7$ D、把① $\times 2$ 整体代入②得： $- 2 - y = 1$

查看试题解析
8. 如图，AB∥CD，BF平分∠ABE，且BF∥DE，则∠ABE与∠D的关系是（　　）

A、∠ABE=3∠D B、∠ABE+∠D=90° C、∠ABE+3∠D=180° D、∠ABE=2∠D

查看试题解析
9. 从一副扑克牌中任意抽出1张牌，抽得下列牌中的概率最大的是（）

A、小王 B、大王 C、10 D、黑桃

查看试题解析
10. 若二元一次方程3x﹣y=﹣7，x+3y=1，y=kx+9有公共解，则k的取值为（）

A、3 B、﹣3 C、﹣4 D、4

查看试题解析
11. 如图是郝老师的某次行车路线，总共拐了三次弯，最后行车路线与开始的路线是平行的，已知第一次转过的角度 $120 °$ ，第三次转过的角度 $135 °$ ，则第二次转过的角度是（）

A、 $75 °$ B、 $120 °$ C、 $135 °$ D、无法确定

查看试题解析
12. 下列说法中正确的是（）

A、通过多次试验得到某事件发生的频率等于这一事件发生的概率 B、某人前 9 次掷出的硬币都是正面朝上，那么第 10 次掷出的硬币反面朝上的概率一定大于正面朝上的概率 C、不确定事件的概率可能等于 1 D、试验估计结果与理论概率不一定一致

查看试题解析

二、填空题

13. 如图，用一根吸管吸吮烧杯中的豆浆，图2是其截面图，纸杯的上底面a与下底面b平行，c表示吸管，若∠1的度数为104°，则∠2的度数为．

查看试题解析
14. 如图，直线 $l_{1}$ ： $y = x + 2$ 与直线 $l_{2}$ ： $y = k x + b$ 相交于点P（m，4），则方程组 ${\begin{matrix} y = x + 2 \\ y = k x + b \end{matrix}$ 的解是．

查看试题解析
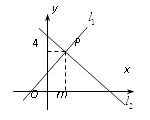15. 某十字路口设有交通信号灯，东西向信号灯的开启规律如下：红灯开启30秒后关闭，紧接着黄灯开启3秒后关闭，再紧接着绿灯开启42秒，按此规律循环下去.如果不考虑其他因素，当一辆汽车沿东西方向随机地行驶到该路口时，遇到红灯的概率是．

查看试题解析
16. 用白铁皮做罐头盒，每张铁皮可制盒身25个，或制盒底40个，一个盒身可以和两个盒底可制成一个罐头盒.现有36张白铁皮，设用x张制盒身，y张制盒底，恰好配套制成罐头盒，根据题意，可列方程组.

查看试题解析
17. 如图，BD、CE为△ABC的两条角平分线，则图中∠1、∠2、∠A之间的关系为.

查看试题解析
18. 现有八个大小相同的矩形，可拼成如图1、2所示的图形，在拼图2时，中间留下了一个边长为2的小正方形，则每个小矩形的面积是.

查看试题解析

三、解答题

19.

(1)、用代入法解方程组： ${\begin{array}{l} x - y = 3 \\ 7 x + 5 y = - 9 \end{array}$

(2)、用加减法解方程组： ${\begin{array}{l} \frac{x}{2} + \frac{y}{3} = 2 \\ 2 (x + 3) - 3 y = 1 \end{array}$

查看试题解析
20. 完成下列推理，并填写完理由
已知，如图，∠BAE+∠AED=180°，∠M=∠N，

试说明： $∠ 1 = ∠ 2$

解：∵∠BAE＋∠AED＝180º（已知）

∴   ▲    ∥   ▲    （   ▲    ）

∴∠BAE＝（两直线平行，内错角相等）

又∵∠M＝∠N （已知）

∴   ▲    ∥   ▲    （   ▲    ）

∴∠NAE＝   ▲    （   ▲    ）

∴∠BAE－∠NAE＝   ▲    （   ▲    ）

即∠1＝∠2

查看试题解析
21. 甲、乙两人玩“锤子、石头、剪子、布”游戏．他们在不透明的袋子中放入形状、大小均相同的19张卡片，其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为3、4、5、7，两人各随机摸出一张卡片（先摸者不放回）来比胜负，并约定：“锤子”胜“石头”和“剪子”，“石头”胜“剪子”，“剪子”胜“布”，“布”胜“锤子”和“石头”，同种卡片不分胜负．

(1)、若甲先摸，他摸出“石头”的概率是多少？

(2)、若甲先摸出了“石头”，则乙获胜的概率是多少？

(3)、若甲先摸，则他先摸出哪种卡片获胜的可能性最大？

查看试题解析
22. 小明准备完成题目：解方程组 ${\begin{array}{l} x - y = 4 \\ □ x + y = - 8 \end{array}$ ，发现系数“□”印刷不清楚．

(1)、他把“□”猜成3，请你解此时的方程组 ${\begin{array}{l} x - y = 4 \\ 3 x + y = - 8 \end{array}$ ．

(2)、张老师说：你在（1）中猜错了，我看到该题的正确答案里有结论： $x$ ， $y$ 互为相反数．依此说法，问原题中的“□”是多少？

查看试题解析
23. 如图，∠α和∠β的度数满足方程组 ${\begin{array}{l} 2 ∠ α + ∠ β = 235^{°} \\ ∠ β - ∠ α = 70^{°} \end{array}$ ，且CD∥EF，AC⊥AE．

(1)、求∠α和∠β的度数．

(2)、求∠C的度数．

查看试题解析
24. 已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物，计划同时租用A型车a辆和B型车b辆,一次运完，且每辆车都满载货物.根据以上信息解答下列问题：

(1)、1辆A型车和1辆B型车载满货物一次分别可运货物多少吨？

(2)、请帮助物流公司设计租车方案

(3)、若A型车每辆车租金每次100元，B型车每辆车租金每次120元.请选出最省钱的租车方案，并求出最少的租车费.

查看试题解析
25. 如图所示，在△ABC中，点D、E、F分别是AB、AC、BC上的点，且∠ADE=90°，∠DEF=90°，点P是FC上一点，直线DP交直线EF于点G，试探究∠BDP与∠EGP之间的数量关系．

(1)、请你完成这道思考题；

(2)、若将题中的条件“∠ADE=90°，∠DEF=90°，点P是FC上一点”改为“∠AED=∠C，∠B=∠DEF，点P是线段BC上一点（点P不与点F重合）”，其他条件均不变，则（1）中的结论是否仍然成立？请在备用图上画出图形，并说明理由．

查看试题解析