山东省青岛市西海岸新区、黄岛区2019-2020学年七年级下学期数学期中试卷
试卷更新日期:2021-04-14 类型:期中考试
一、单选题
-
1. 计算(-a3)2的结果是( )A、-a5 B、a5 C、a6 D、-a62. 芯片是手机、电脑等高科技产品最核心的部件,更小的芯片意味着更高的性能.目前我国芯片的量产工艺已达到14纳米,已知14纳米为0.000000014米,则0.000000014科学记数法表示为( )A、1.4×10﹣8 B、1.4×10﹣9 C、1.4×10﹣10 D、14×10﹣93. 在实验课上,小亮利用同一块木板测得小车从不同高度(h)与下滑的时间(t)的关系如下表:
支撑物高h(cm)
10
20
30
40
50
…
下滑时间t(s)
3.25
3.01
2.81
2.66
2.56
…
以下结论错误的是( )
A、当h=40时,t约2.66秒 B、随高度增加,下滑时间越来越短 C、估计当h=80cm时,t一定小于2.56秒 D、高度每增加了10cm,时间就会减少0.24秒4. 下列各式中计算正确的是( )A、(a+b)(b﹣a)=a2﹣b2 B、(﹣m﹣n)2=m2+2mn+n2 C、2m3÷m3=2m D、(﹣bc)4÷(﹣bc)2=﹣b2c25. 如图,直线AB∥CD,且AC⊥AD,∠ACD=58°,则∠BAD的度数为( ) A、29° B、30° C、32° D、58°6. 如图,下列不能判定DF∥AC的条件是( )
A、29° B、30° C、32° D、58°6. 如图,下列不能判定DF∥AC的条件是( ) A、∠A=∠BDF B、∠2=∠4 C、∠1=∠3 D、∠A+∠ADF=180°7. 把一张有一组对边平行的纸条,按如图所示的方式析叠,若∠EFB=35°,则下列结论错误的是( )
A、∠A=∠BDF B、∠2=∠4 C、∠1=∠3 D、∠A+∠ADF=180°7. 把一张有一组对边平行的纸条,按如图所示的方式析叠,若∠EFB=35°,则下列结论错误的是( ) A、∠C'EF=35° B、∠AEC=120° C、∠BGE=70° D、∠BFD=110°8. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A、∠C'EF=35° B、∠AEC=120° C、∠BGE=70° D、∠BFD=110°8. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( ) A、
A、 B、
B、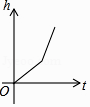 C、
C、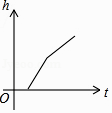 D、
D、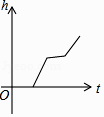
二、填空题
-
9. 计算:(π﹣3)0﹣(﹣ )﹣2+(﹣1)2020= .10. 有一个角的补角为125°,则这个角的余角是 °.11. am=6,an=3,则am﹣2n= .12. 已知实数a,b满足a+b=5,ab=﹣3,则a2+b2的值为 .13. 将一个等腰直角三角形的直角顶点和一个锐角顶点按如图方式分别放在直线a,b上,若a∥b,∠1=24°,则∠2的度数为°.
 14. 如图,现有A,C两类正方形卡片和B类长方形卡片各若干张,用它们可以拼成一些新的长方形.如果要拼成一个长为(3a+b),宽为(a+2b)的长方形,那么需要B类长方形卡片张.
14. 如图,现有A,C两类正方形卡片和B类长方形卡片各若干张,用它们可以拼成一些新的长方形.如果要拼成一个长为(3a+b),宽为(a+2b)的长方形,那么需要B类长方形卡片张. 15. 如图,已知AB∥DE,∠ABC=76°,∠CDE=150°,则∠BCD的度数为°.
15. 如图,已知AB∥DE,∠ABC=76°,∠CDE=150°,则∠BCD的度数为°. 16. 如图所示的图形都由同样大小的小圆圈按一定规律所组成的,若按此规律排列下去,则第n个图形中有个小圆圈.
16. 如图所示的图形都由同样大小的小圆圈按一定规律所组成的,若按此规律排列下去,则第n个图形中有个小圆圈.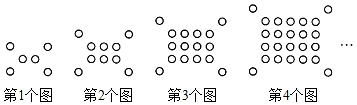
三、解答题
-
17. 如图,AB是某条河上的一座桥,现要在河的下游点C处再建一座与AB平行的桥CD,请用直尺和圆规画出CD的方向.
 18. 计算:(1)、(﹣2a2b)2•ab2÷(﹣a3b);(2)、(x﹣1)(x+1)(x2+1);(3)、20202﹣2022×2018(用乘法公式计算);(4)、(a﹣b﹣3)(a﹣b+3).19. 先化简,再求值[(x﹣2y)2﹣(x+y)(x﹣3y)]÷(﹣y),其中x=﹣1,y= .20. 完成下面的证明.
18. 计算:(1)、(﹣2a2b)2•ab2÷(﹣a3b);(2)、(x﹣1)(x+1)(x2+1);(3)、20202﹣2022×2018(用乘法公式计算);(4)、(a﹣b﹣3)(a﹣b+3).19. 先化简,再求值[(x﹣2y)2﹣(x+y)(x﹣3y)]÷(﹣y),其中x=﹣1,y= .20. 完成下面的证明.已知:如图, 与 互补, ,
求证:

证明: 与 互补
即 ,(已知)
▲ // ▲ ( ▲ )
.( ▲ )
又 ,(已知)
,即 .(等式的性质)
▲ // ▲ (内错角相等,两直线平行)
.( ▲ )
21. 如图所示,在一个边长为10cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化. (1)、在这个变化过程中,自变量.因变量各是什么?(2)、如果小正方形的边长为xcm,图中阴影部分的面积ycm2 , 请写出y与x的关系式;(3)、当小正方形的边长由1cm变化到3cm时,阴影部分的面积发生了怎样的变化?22. 如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)、在这个变化过程中,自变量.因变量各是什么?(2)、如果小正方形的边长为xcm,图中阴影部分的面积ycm2 , 请写出y与x的关系式;(3)、当小正方形的边长由1cm变化到3cm时,阴影部分的面积发生了怎样的变化?22. 如图,∠AGF=∠ABC,∠1+∠2=180°. (1)、试判断BF与DE的位置关系,并说明理由;(2)、若BF⊥AC,∠2=145°,求∠AFG的度数.23. 阅读理解:
(1)、试判断BF与DE的位置关系,并说明理由;(2)、若BF⊥AC,∠2=145°,求∠AFG的度数.23. 阅读理解:下面的图象表示2m的个位数字随m(m为正整数)变化的规律.请解答下列问题:
 (1)、根据图象回答下列问题:
(1)、根据图象回答下列问题:当m=4n(n为正整数)时,2m的个位数字是;
当m=4n+1(n为正整数)时,2m的个位数字是;
当m=4n+2(n为正整数)时,2m的个位数字是;
当m=4n+3(n为正整数)时,2m的个位数字是;
(2)、求:(2+1)(22+1)(24+1)(28+1)+1的个位数字.(3)、求:(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)的个位数字.24. 如图①,在长方形ABCD中,AB=10cm,BC=8cm,点P从A出发,沿A→B→C→D路线运动,到D停止;点P出发时的速度为每秒1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,△APD的面积S(cm2)与x(s)的函数关系图象.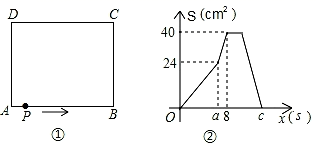 (1)、根据题目中提供的信息,求出图②中a,b,c的值;(2)、设点P运动的路程为y(cm).
(1)、根据题目中提供的信息,求出图②中a,b,c的值;(2)、设点P运动的路程为y(cm).①7s时,求y的值;
②请写出当点P改变速度后,y与x的函数关系式;
(3)、当点P出发后几秒时,△APD的面积S是长方形ABCD面积的 ?