山东省济南市长清区2019-2020学年七年级下学期数学期中试卷
试卷更新日期:2021-04-14 类型:期中考试
一、单选题
-
1. 在以下回收、绿色食品、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、a3•a2=a6 B、3a•4a=12a C、(﹣a3)4=a12 D、a8÷a2=a43. 数0.0000025用科学记数法表示为( )A、2.5×106 B、0.25×10﹣5 C、2.5×10﹣6 D、25×10﹣74. 下列事件是必然事件的是( )A、掷一枚质地均匀的硬币,一定正面向上 B、从一副扑克中任意抽出一张是黑桃 C、在一个三角形中,任意两边之和大于第三边 D、如果a2=b2 , 那么a=b5. 如图,已知AB∥CD,AD平分∠BAE,∠D=40°,则∠DAE的度数是( )
2. 下列计算正确的是( )A、a3•a2=a6 B、3a•4a=12a C、(﹣a3)4=a12 D、a8÷a2=a43. 数0.0000025用科学记数法表示为( )A、2.5×106 B、0.25×10﹣5 C、2.5×10﹣6 D、25×10﹣74. 下列事件是必然事件的是( )A、掷一枚质地均匀的硬币,一定正面向上 B、从一副扑克中任意抽出一张是黑桃 C、在一个三角形中,任意两边之和大于第三边 D、如果a2=b2 , 那么a=b5. 如图,已知AB∥CD,AD平分∠BAE,∠D=40°,则∠DAE的度数是( )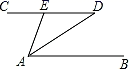 A、20° B、40° C、60° D、80°6. 点D、E分别在线段AB、AC上,CD与BE相交于点O,已知AE=AD,添加以下哪一个条件不能判定△ABE≌△ACD( )
A、20° B、40° C、60° D、80°6. 点D、E分别在线段AB、AC上,CD与BE相交于点O,已知AE=AD,添加以下哪一个条件不能判定△ABE≌△ACD( ) A、∠B=∠C B、∠BEA=∠CDA C、BE=CD D、AB=AC7. 李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A、∠B=∠C B、∠BEA=∠CDA C、BE=CD D、AB=AC7. 李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( ) A、金额 B、数量 C、单价 D、金额和数量8. 已知三角形三边长分别为5、a、9,则数a可能是( )A、4 B、6 C、14 D、159. 如图,在△ABC中,∠B=32°,∠BAC的平分线AD交BC于点D,若DE垂直平分AB,则∠C的度数为( )
A、金额 B、数量 C、单价 D、金额和数量8. 已知三角形三边长分别为5、a、9,则数a可能是( )A、4 B、6 C、14 D、159. 如图,在△ABC中,∠B=32°,∠BAC的平分线AD交BC于点D,若DE垂直平分AB,则∠C的度数为( )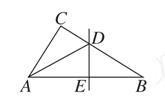 A、90° B、84° C、64° D、58°10. 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率是( )
A、90° B、84° C、64° D、58°10. 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率是( )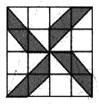 A、 B、 C、 D、11. 如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以A,P,B为顶点的三角形面积为y,则选项图象能大致反映y与x的函数关系的是( )
A、 B、 C、 D、11. 如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以A,P,B为顶点的三角形面积为y,则选项图象能大致反映y与x的函数关系的是( )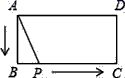 A、
A、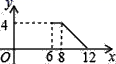 B、
B、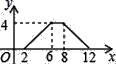 C、
C、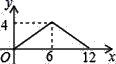 D、
D、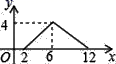 12. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①DE=CD;②AD平分∠CDE;③∠BAC=∠BDE;④BE+AC=AB,其中正确的是( )
12. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①DE=CD;②AD平分∠CDE;③∠BAC=∠BDE;④BE+AC=AB,其中正确的是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 计算:x(x﹣3)= .14. 在一个不透明的袋子中装有5个除颜色外完全相同的小球,其中2个蓝色,3个红色,从袋中随机摸出一个,摸到的是蓝色小球的概率是.15. 若x2﹣mx+9是个完全平方式,则m的值是 .16. 已知等腰三角形的两边长是3cm和6cm,则这个等腰三角形的周长是 cm.17. 某水果店卖出的香蕉数量(千克)与售价(元)之间的关系如下表:
数量(千克)
0.5
1
1.5
2
2.5
3
3.5
…
售价(元)
1.5
3
4.5
6
7.5
9
10.5
…
如果卖出的香蕉数量用x(千克)表示,售价用y(元)表示,则y与x的关系式为 .
18. 如图,依据尺规作图的痕迹,计算∠α=°.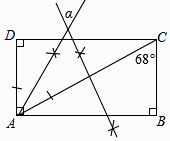
三、解答题
-
19.(1)、计算:(﹣1)2020+(﹣2)﹣2﹣(3.14﹣π)0;(2)、化简:(x+2)2﹣(x+1)(x﹣1).20. 先化简,再求值:(a2b﹣2ab2﹣b)÷b+(b﹣a)(b+a),其中a= ,b=1.21. 填空:如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系:

解:CD⊥AB
∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠ ▲ =90°(垂直定义)
∴DG∥AC,( ▲ )
∴∠2=∠ ▲ .(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠1=∠ ▲ (等量代换)
∴EF∥ ▲ (同位角相等,两直线平行)
∴∠AEF=∠ADC,( ▲ )
∵EF⊥AB,
∴∠AEF=90°
∴∠ADC=90°
即:CD⊥AB.
22. 已知,如图,AB=CD,AB∥CD,BE=FD,问△ABF与△CDE全等吗? 23. 如图(1),方格图中每个小正方形的边长为1,点A、B、C都是格点.
23. 如图(1),方格图中每个小正方形的边长为1,点A、B、C都是格点. (1)、画出 关于直线MN对称的 ;(2)、写出 的长度;24. 暑假将至,某商场为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被均匀地分为20份),并规定:顾客每 200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.若某顾客购物300元.
(1)、画出 关于直线MN对称的 ;(2)、写出 的长度;24. 暑假将至,某商场为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被均匀地分为20份),并规定:顾客每 200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.若某顾客购物300元. (1)、求他此时获得购物券的概率是多少?(2)、他获得哪种购物券的概率最大?请说明理由.25. 小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)、求他此时获得购物券的概率是多少?(2)、他获得哪种购物券的概率最大?请说明理由.25. 小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题: (1)、小明家到学校的路程是米.(2)、小明在书店停留了分钟.(3)、本次上学途中,小明一共行驶了米.一共用了分钟.(4)、我们认为骑单车的速度超过 300 米/分就超过了安全限度.问:在整个上学途中哪个时间段小明的骑车速度最快,最快速度为多少,在安全限度内吗?26. 如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)、小明家到学校的路程是米.(2)、小明在书店停留了分钟.(3)、本次上学途中,小明一共行驶了米.一共用了分钟.(4)、我们认为骑单车的速度超过 300 米/分就超过了安全限度.问:在整个上学途中哪个时间段小明的骑车速度最快,最快速度为多少,在安全限度内吗?26. 如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE. (1)、求证:DE=BD+CE.(2)、如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.27. 如图,已知在△ABC中,AB=AC,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.
(1)、求证:DE=BD+CE.(2)、如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.27. 如图,已知在△ABC中,AB=AC,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动. (1)、用含t的式子表示PC的长为;(2)、若点Q的运动速度与点p的运动速度相等,当t=2时,三角形BPD与三角形CQP是否全等,请说明理由;(3)、若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,
(1)、用含t的式子表示PC的长为;(2)、若点Q的运动速度与点p的运动速度相等,当t=2时,三角形BPD与三角形CQP是否全等,请说明理由;(3)、若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,