云南省昭通市昭阳区2019-2020学年八年级下学期数学期中试卷

试卷更新日期：2021-04-14 类型：期中考试

进入出卷网下载

一、填空题

1. 实数 $- \sqrt{2}$ 的相反数是.

查看试题解析
2. 分解因式：2x²﹣8=

查看试题解析
3. 一直角三角形的一直角边及斜边长分别是 $6 c m$ 和 $8 c m,$ 则这个三角形的第三边长 $c m$ ．

查看试题解析
4. 菱形周长为40 cm，它的一条对角线长12 cm，则菱形的面积为cm²

查看试题解析
5. 如图，在 $Rt Δ ABC$ 中， $∠ B = 90 °$ ， $AB = 30$ ， $BC = 40$ ，将 $Δ ABC$ 折叠，使点 $B$ 恰好落在边 $AC$ 上，与点 $B'$ 重合， $AE$ 为折痕，则 $EB'=$ .

查看试题解析
6. 已知点 $O$ 为水平直线 $A B$ 上一点（不与点 $A 、 B$ 重合），点 $D 、 E$ 在直线 $A B$ 的上方， $O D ⊥ O E ，$ 若 $∠ A O D = 50 °$ ，则 $∠ B O E$ 的度数为．

查看试题解析

二、单选题

7. 要使二次根式 $\sqrt{x - 3}$ 有意义，则x的取值范围是（）

A、x≠3 B、x＞3 C、x＜3 D、x≥3

查看试题解析
8. 下列根式中，与 $\sqrt{12}$ 为同类二次根式的是（）．

A、 $\sqrt{3}$ B、 $\sqrt{2}$ C、 $\sqrt{6}$ D、 $\sqrt{32}$

查看试题解析
9. 若 $a ， b$ 为实数，且 $| a + 1 | + \sqrt{b - 1} = 0 ，$ 则 ${(a b)}^{2020}$ 的值是（）

A、 $1$ B、 $- 1$ C、 $2$ D、 $- 2$

查看试题解析
10. 若等边△ABC的边长为4，那么△ABC的面积为（）.

A、 $2 \sqrt{3}$ B、 $4 \sqrt{3}$ C、8 D、4

查看试题解析
11. 如图，任意四边形ABCD各边中点分别是E，F，G，H，若对角线AC，BD的长都为20cm，则四边形EFGH的周长是（）

A、80cm B、40cm C、20cm D、10cm

查看试题解析
12. 如图，在▱ABCD中，已知AD=12cm，AB=8cm，AE平分∠BAD交BC边于点E，则CE的长等于（　）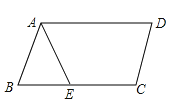　

A、8cm B、6cm C、4cm D、2cm

查看试题解析
13. 如图， $△ A B C$ 中， $A B = A C = 6 ， A E ⊥ A C ， D E$ 垂直平分 $A B$ 于点 $D ，$ 则 $E C$ 的长为（）

A、 $2 \sqrt{3}$ B、 $4 \sqrt{3}$ C、 $2 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析
14. 如图是“赵爽弦图”，由 $4$ 个全等的直角三角形拼成，若大正方形的面积是13，小正方形的面积是1，设直角三角形较长直角边为a，较短直角边为 $b$ ．则a+b的值是（）

A、 $3$ B、 $4$ C、 $5$ D、 $7$

查看试题解析

三、解答题

15. 计算：

(1)、 $2 \sqrt{12} - 6 \sqrt{\frac{1}{3}} + 3 \sqrt{48}$ ；

(2)、 $\sqrt{4} + 2020^{0} - | \sqrt{3} - 2 | + 1$ ．

查看试题解析
16. 已知：a＝2+ $\sqrt{3}$ ，b＝2﹣ $\sqrt{3}$ ，求：①a²+b² ， ② $\frac{a}{b} - \frac{b}{a}$ 的值．

查看试题解析
17. 如图，已知平行四边形 $A B C D$ 中， $A E$ 平分 $∠ B A D ， C F$ 平分 $∠ B C D$ ，分别交 $B C 、 A D$ 于点 $E 、 F ，$ 求证： $A E = C F$ ．

查看试题解析
18. 在正方形ABCD中，对角线BD所在的直线上有两点E、F满足BE=DF，连接AE、AF、CE、CF，如图所示．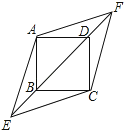

(1)、求证：△ABE≌△ADF；

(2)、试判断四边形AECF的形状，并说明理由．

查看试题解析
19. 求知中学有一块四边形的空地ABCD，如下图所示，学校计划在空地上种植草皮，经测量∠A=90°，AB =3m，BC =12m，CD =13m，DA= 4m，若每平方米草皮需要200元，问学校需要投入多少资金买草皮？

查看试题解析
20. 先化简，再求值：（1﹣ $\frac{1}{x + 2}$ ）÷ $\frac{x^{2} + 2 x + 1}{2 x + 4}$ ，其中x= $\sqrt{2}$ ﹣1．

查看试题解析
21. “褚橙”是云南特色水果之一，不仅味道独具一格，营养价值也十分高．某水果店在开业期间购进甲、乙两种型号的“褚橙”共 $200$ 箱．为了提升销量，对这两种“褚橙”进行打折出售．打折后甲型号“褚橙”每箱 $188$ 元，乙型号“褚橙”每箱 $148$ 元，这两种“褚橙”全部销售完后．销售总收入为 $32800$ 元．请问甲、乙两种型号的“褚橙”各有多少箱？

查看试题解析
22. 如图，平行四边形ABCD的对角线AC，BD相交于O，过点O的直线EF分别交AB，CD于E，F，连结DE，BF．
求证：四边形DEBF是平行四边形．

查看试题解析
23. 如图，在矩形ABCD中，AB=1cm，AD=3cm，点Q从A点出发，以1cm/s的速度沿AD向终点D运动，点P从点C出发，以1cm/s的速度沿CB向终点B运动，当这两点中有一点到达自己的终点时，另一点也停止运动，两点同时出发，运动了t秒.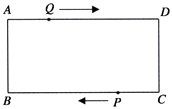

(1)、当0＜t＜3，判断四边形BQDP的形状，并说明理由；

(2)、求四边形BQDP的面积S与运动时间t的函数关系式；

(3)、求当t为何值时，四边形BQDP为菱形.

查看试题解析