云南省临沧市云县2019-2020学年八年级下学期数学期中试卷

试卷更新日期：2021-04-14 类型：期中考试

进入出卷网下载

一、填空题

1. 计算 $\sqrt{2}$ ×2 $\sqrt{2}$ ＝．

查看试题解析
2. 一个直角三角形的两条直角边长分别为3，4，则第三边为．

查看试题解析
3. 要使式子 $\sqrt{x + 5}$ 有意义，则x的取值范围是．

查看试题解析
4. 如图，在△ABC中，D、E分别为AB、AC边的中点，若DE=2，则BC边的长为．

查看试题解析
5. 如图，一棵大树在离地面3m、5m两处折成三段，中间一段AB恰好与地面平行，大树顶部落在离大树底部6m处，则大树折断前的高度是．

查看试题解析
6. 菱形 ABCD 的对角线 AC=4，BD=2，以 AC 为边作正方形 ACEF，则 BF 的长为．

查看试题解析

二、单选题

7. 下列式子是最简二次根式的是（）

A、 $\sqrt{15}$ B、 $\sqrt{1.5}$ C、 $\sqrt{20}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
8. 判断下列各组数能作为直角三角形三边长的是（）

A、3，4，6 B、4，5，7 C、2，3， $\sqrt{7}$ D、7，6， $\sqrt{13}$

查看试题解析
9. 如图，已知菱形ABCD的对角线交于点O，DB=6，AD=5，则菱形ABCD的面积为（）

A、20 B、24 C、30 D、36

查看试题解析
10. 在Rt△ABC中，∠ABC＝90°，D为斜边AC的中点，BD＝5，则AC＝（）

A、5 B、6 C、8 D、10

查看试题解析
11. 下列计算中，正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = \pm 3$ B、 $\sqrt{27} \div \sqrt{3} = 9$ C、 $\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{8} \times \sqrt{6}}{\sqrt{2}} = \sqrt{4} \times \sqrt{3}$

查看试题解析
12. 不能判定四边形ABCD为平行四边形的条件是（）

A、AB∥CD，AD="BC" ； B、AB∥CD，∠A=∠C； C、AD∥BC，AD="BC" ； D、∠A=∠C，∠B=∠D

查看试题解析
13. 如图，延长矩形ABCD的边BC至点E，使CE＝CA，连接AE，若∠BAC＝52°，则∠E的度数是（）

A、18° B、19° C、20° D、40°

查看试题解析
14. 已知a＝2+ $\sqrt{3}$ ，b＝2﹣ $\sqrt{3}$ ，则a²+b²的值为（）

A、12 B、14 C、16 D、18

查看试题解析

三、解答题

15. 计算： $\sqrt{24} + {(\sqrt{6} - 3)}^{0} - \sqrt{\frac{3}{2}} + {(2 \sqrt{2})}^{2}$

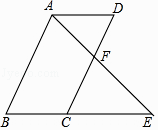
查看试题解析
16. 国家交通法规定：小汽车在城市街道上行驶速度不得超过60km/h，一辆小汽车在一条城市街道上由西向东行驶，此时在小汽车正南方向25m处有一个车速检测仪，过了4s后，测得小汽车距离测速仪65m．这辆小汽车超速了吗？通过计算说明理由（1m/s＝3.6km/h）

查看试题解析
17. 如图，四边形ABCD为平行四边形，F是CD的中点，连接AF并延长与BC的延长线交于点E．求证：BC=CE．

查看试题解析
18. 如图，在四边形ABCD中，AB＝1，AD＝ $\sqrt{3}$ ，BD＝2，∠ABC+∠ADC＝180°，CD＝ $\sqrt{2}$ ．求四边形ABCD的面积．

查看试题解析
19. 先化简，再求值： $(1 + \frac{1}{a - 1}) \div \frac{a^{2} + 2 a + 1}{a^{2} - 1}$ ，其中a＝ $\sqrt{3}$ ﹣1．

查看试题解析
20. 如图，在笔直的高速路旁边有A、B两个村庄，A村庄到公路的距离AC＝8km ， B村庄到公路的距离BD＝14km ，测得C、D两点的距离为20km ，现要在CD之间建一个服务区E ，使得A、B两村庄到E服务区的距离相等，求CE的长．

查看试题解析
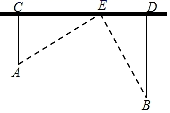21. 如图，在四边形ABCD中，AD∥BC，∠ABC＝∠ADC，对角线AC、BD相交于点O，OA＝OB．

(1)、求证：四边形ABCD是矩形；

(2)、若AB＝5，∠AOB＝60°，求BC的长．

查看试题解析
22. 观察下列等式
等式一： $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；

等式二： $\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；

等式三： $\frac{1}{\sqrt{4} + \sqrt{3}} = \frac{\sqrt{4} - \sqrt{3}}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})} = \sqrt{4} - \sqrt{3} = 2 - \sqrt{3}$ ；

……；

解决下列问题：

(1)、化简： $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ ；

(2)、若有理数a、b满足 $\frac{a}{\sqrt{2} + 1} + \frac{b}{\sqrt{2 - 1}} = - 1 + 2 \sqrt{2}$ ，求a＋b的值．

查看试题解析
23. 如图，四边形ABCD是菱形，∠ABC＝60°，AB＝10，连接BD，点P是BC上的点，连接AP，交BD于点E，连接EC

(1)、求证：△ABE≌△CBE；

(2)、求菱形ABCD的面积；

(3)、当点P在线段BC的延长线上时，是否存在点P，使得△PEC是直角三角形？若存在，求出BP的长；若不存在，请说明理由．

查看试题解析