山东省滕州市2019-2020学年八年级下学期数学期中试卷
试卷更新日期:2021-04-14 类型:期中考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如果一个等腰三角形的一个内角等于40°,则该等腰三角形的底角的度数为( ).A、40° B、70° C、40°或70° D、都不是3. 若 ,则下列式子中正确的是( )A、 B、 C、 D、4. 下列各式从左到右因式分解正确的是( )A、 B、 C、 D、5. 如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为( )
2. 如果一个等腰三角形的一个内角等于40°,则该等腰三角形的底角的度数为( ).A、40° B、70° C、40°或70° D、都不是3. 若 ,则下列式子中正确的是( )A、 B、 C、 D、4. 下列各式从左到右因式分解正确的是( )A、 B、 C、 D、5. 如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为( ) A、8 B、7 C、6 D、56. 如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(﹣1,0),AC=2.将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是( )
A、8 B、7 C、6 D、56. 如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(﹣1,0),AC=2.将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是( )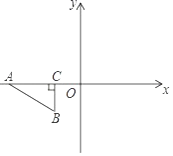 A、(2,2) B、(1,2) C、(﹣1,2) D、(2,﹣1)7. 观察图中的函数图象,则关于 的不等式 的解集为( )
A、(2,2) B、(1,2) C、(﹣1,2) D、(2,﹣1)7. 观察图中的函数图象,则关于 的不等式 的解集为( ) A、 B、 C、 D、8. 在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A、 B、 C、 D、8. 在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( ) A、点M B、点N C、点P D、点Q9. 如图,天平右盘中的每个砝码的质量为10g,则物体M的质量m(g)的取值范围在数轴上可表示为( )
A、点M B、点N C、点P D、点Q9. 如图,天平右盘中的每个砝码的质量为10g,则物体M的质量m(g)的取值范围在数轴上可表示为( ) A、
A、 B、
B、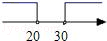 C、
C、 D、
D、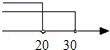 10. 如图,将△AOB绕点O按逆时针方向旋转 后得到△COD,若 ,则 的度数是( )
10. 如图,将△AOB绕点O按逆时针方向旋转 后得到△COD,若 ,则 的度数是( )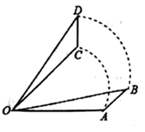 A、 B、 C、 D、11. 如图,O是△ABC的两条垂直平分线的交点,∠BAC=70°,则∠BOC=( )
A、 B、 C、 D、11. 如图,O是△ABC的两条垂直平分线的交点,∠BAC=70°,则∠BOC=( )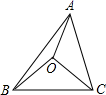 A、120° B、125° C、130° D、140°12. 如图所示,在 中, 是 的平分线, 于点 , .给出下列结论:① 是等腰三角形;② 是等腰三角形;③ ;④ .其中正确的是( )
A、120° B、125° C、130° D、140°12. 如图所示,在 中, 是 的平分线, 于点 , .给出下列结论:① 是等腰三角形;② 是等腰三角形;③ ;④ .其中正确的是( ) A、②③④ B、①②③④ C、②③ D、③
A、②③④ B、①②③④ C、②③ D、③二、填空题
-
13. 若 的 倍与 的和大于 ,则满足条件的 的最小整数为 .14. 长和宽分别是a,b的长方形的周长为16,面积为9,则a2b+ab2的值为 .15. 下面三个命题: 底边和顶角对应相等的两个等腰三角形全等; 两边及其中一边上的中线对应相等的两个三角形全等; 斜边和斜边上的中线对应相等的两个直角三角形全等,其中正确的命题的序号为 .16. 如图,将直角三角形ABC沿着点B到点C的方向平移到三角形DEF的位置,已知AB=10,HD=4,CF=6,则阴影部分的面积是.
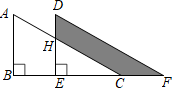 17. 在 中, 的垂直平分线交AB于点D,交AC于点E,已知 的周长为30,则BC= .
17. 在 中, 的垂直平分线交AB于点D,交AC于点E,已知 的周长为30,则BC= . 18. 在 中, ,以 的边 为一边的等腰三角形,它的第三个顶点在 的斜边 上,则这个等腰三角形的腰长为.
18. 在 中, ,以 的边 为一边的等腰三角形,它的第三个顶点在 的斜边 上,则这个等腰三角形的腰长为.三、解答题
-
19. 分解因式:(1)、(2)、20. 若关于 的二元一次方程组 的解满足 ,求出满足条件的 的所有正整数数值.21. 如图,在正方形网格中, 的三个顶点都在格点上,点 的坐标分别为
 (1)、画出 关于原点 对称的(2)、平移 ,使点 移动到点 ,画出平移后的 ,并写出点 的坐标;(3)、 与 成中心对称,写出其对称中心的坐标.22. 如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)、画出 关于原点 对称的(2)、平移 ,使点 移动到点 ,画出平移后的 ,并写出点 的坐标;(3)、 与 成中心对称,写出其对称中心的坐标.22. 如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F. (1)、若∠C=36°,求∠BAD的度数.(2)、若点E在边AB上,EF//AC叫AD的延长线于点F.求证:FB=FE.23. 如图所示,在 和 中, ,点 是 的中点, ,垂足为 ,且
(1)、若∠C=36°,求∠BAD的度数.(2)、若点E在边AB上,EF//AC叫AD的延长线于点F.求证:FB=FE.23. 如图所示,在 和 中, ,点 是 的中点, ,垂足为 ,且 (1)、求证:△ 是等腰直角三角形;(2)、若 ,求 的长.24.(1)、解不等式组 并把解集表示在数轴上;(2)、现有 两种商品,每件单价分别为 元, 元如果小静准备购买 两种商品共 件,总费用不超过 元,且不低于 元,问有几种购买方案?哪种方案费用最低?25. [问题情境]在课堂上,学习兴趣小组对一道数学问题进行了深入探究:在 中, ,点 是 的中点,连接 .(1)、[探索发现]
(1)、求证:△ 是等腰直角三角形;(2)、若 ,求 的长.24.(1)、解不等式组 并把解集表示在数轴上;(2)、现有 两种商品,每件单价分别为 元, 元如果小静准备购买 两种商品共 件,总费用不超过 元,且不低于 元,问有几种购买方案?哪种方案费用最低?25. [问题情境]在课堂上,学习兴趣小组对一道数学问题进行了深入探究:在 中, ,点 是 的中点,连接 .(1)、[探索发现]如图①, 与 的数量关系是
 (2)、[猜想验证]
(2)、[猜想验证]如图②,若 是线段 上动点(点 不与点 重合),连接 ,将线段 绕点 逆时针旋转 ,得到线段 ,连接BF,请猜想 三者之间的数量关系,并证明你的结论;
 (3)、[拓展延伸]
(3)、[拓展延伸]若点 是线段 延长线上一动点,按照(2)中的作法,请在图③中补全图形,并探究 三者之间的数量关系.
