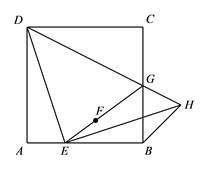山东省临沂市沂水县2019-2020学年八年级下学期数学期中试卷
试卷更新日期:2021-04-14 类型:期中考试
一、单选题
-
1. 使二次根式 有意义的 的取值范围是( )A、 B、 C、 D、2. 下列各式中,是最简二次根式的是( )A、 B、 C、 D、3. 如图,点E在正方形ABCD的边AB上,若正方形ABCD的面积是3, ,那么EB的长为( )
 A、1 B、 C、 D、34. 下列运算正确的是( )A、 B、 C、 D、5. 如图,在 中, ,点 , 分别是边 , 的中点,那么 的长为
A、1 B、 C、 D、34. 下列运算正确的是( )A、 B、 C、 D、5. 如图,在 中, ,点 , 分别是边 , 的中点,那么 的长为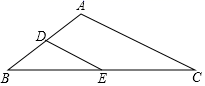 A、2 B、1.5 C、4 D、36. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A、2 B、1.5 C、4 D、36. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( ) A、90° B、60° C、45° D、30°7. 已知直角三角形ABC中, , ,若 ,则AB长为( )A、2 B、3 C、4 D、8. 如图所示□ABCD , 再添加下列某一个条件, 不能判定□ABCD是矩形的是( )
A、90° B、60° C、45° D、30°7. 已知直角三角形ABC中, , ,若 ,则AB长为( )A、2 B、3 C、4 D、8. 如图所示□ABCD , 再添加下列某一个条件, 不能判定□ABCD是矩形的是( ) A、AC=BD B、AB⊥BC C、∠1=∠2 D、∠ABC=∠BCD9. 如图,从一个大正方形中截去面积为 和 的两个正方形,则剩余部分的面积为( )
A、AC=BD B、AB⊥BC C、∠1=∠2 D、∠ABC=∠BCD9. 如图,从一个大正方形中截去面积为 和 的两个正方形,则剩余部分的面积为( )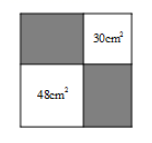 A、 B、 C、 D、10. 如图,在▱ABCD中,AB
A、 B、 C、 D、10. 如图,在▱ABCD中,AB AC,若AB=4,AC=6,则BD的长是( )
AC,若AB=4,AC=6,则BD的长是( )  A、11 B、10 C、9 D、811. 为了研究特殊四边形,李老师制作了这样一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD,并在A与C、B与D两点之间分别用一根橡皮筋拉直固定,课上,李老师右手拿住木条BC,用左手向右推动框架至AB⊥BC(如图2)观察所得到的四边形,下列判断正确的是( )
A、11 B、10 C、9 D、811. 为了研究特殊四边形,李老师制作了这样一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD,并在A与C、B与D两点之间分别用一根橡皮筋拉直固定,课上,李老师右手拿住木条BC,用左手向右推动框架至AB⊥BC(如图2)观察所得到的四边形,下列判断正确的是( ) A、∠BCA=45° B、AC=BD C、BD的长度变小 D、AC⊥BD12. 如图,矩形 中, 是 中点,作 的角平分线交 于 点,若 , ,则 的长度为( )
A、∠BCA=45° B、AC=BD C、BD的长度变小 D、AC⊥BD12. 如图,矩形 中, 是 中点,作 的角平分线交 于 点,若 , ,则 的长度为( ) A、 B、 C、 D、13. 如图,在四边形ABCD中, , , , ,分别以点A,C为圆心,大于 长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为( )
A、 B、 C、 D、13. 如图,在四边形ABCD中, , , , ,分别以点A,C为圆心,大于 长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为( )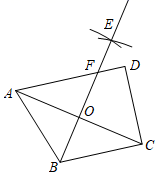 A、 B、6 C、 D、814. 将四根长度相等的细木条首尾顺次相接,用钉子钉成四边形ABCD,转动这个四边形可以使它的形状改变.当 时,如图(1),测得 ;当 时,如图(2),此时AC的长为( )
A、 B、6 C、 D、814. 将四根长度相等的细木条首尾顺次相接,用钉子钉成四边形ABCD,转动这个四边形可以使它的形状改变.当 时,如图(1),测得 ;当 时,如图(2),此时AC的长为( ) A、 B、 C、3 D、
A、 B、 C、3 D、二、填空题
-
15. 若 ,则 的值为 .16. 如图,在平行四边形ABCD中, , ,则 .
 17. 如图,点P(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的坐标为.
17. 如图,点P(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的坐标为. 18. 如图,在菱形ABCD中,过点C作 交对角线 于点 ,且 ,若 ,则 .
18. 如图,在菱形ABCD中,过点C作 交对角线 于点 ,且 ,若 ,则 . 19. 在数学课上,老师提出如下问题:如图1,将锐角三角形纸片ABC经过两次折叠,得到边AB,BC,CA上的点D,E,F.折叠方法如下:如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D;(2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.则下列结论:①四边形DECF一定是矩形,②四边形DECF一定是菱形,③四边形DECF一定是正方形.其中错误的是(填序号)
19. 在数学课上,老师提出如下问题:如图1,将锐角三角形纸片ABC经过两次折叠,得到边AB,BC,CA上的点D,E,F.折叠方法如下:如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D;(2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.则下列结论:①四边形DECF一定是矩形,②四边形DECF一定是菱形,③四边形DECF一定是正方形.其中错误的是(填序号)
三、解答题
-
20. 计算:(1)、(2)、21.
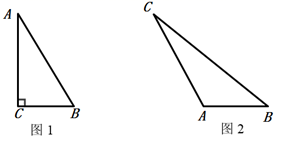 (1)、如图1,在 中, , , ,求 的长.(2)、如图2,在 中, , , ,求 的长.22. 在平行四边形ABCD中,用尺规作图 的角平分线(不用写过程,留下作图痕迹),交DC边于点H,若 , ,求平行四边形ABCD的周长.
(1)、如图1,在 中, , , ,求 的长.(2)、如图2,在 中, , , ,求 的长.22. 在平行四边形ABCD中,用尺规作图 的角平分线(不用写过程,留下作图痕迹),交DC边于点H,若 , ,求平行四边形ABCD的周长. 23. 如图, 是 的边 上一点, , 交 于点 ,若 .
23. 如图, 是 的边 上一点, , 交 于点 ,若 . (1)、求证:四边形CDBE是平行四边形;(2)、若 , ,求四边形CDBE的面积.24.(1)、填空:(只填写符号: )
(1)、求证:四边形CDBE是平行四边形;(2)、若 , ,求四边形CDBE的面积.24.(1)、填空:(只填写符号: )①当 , 时, ;
②当 , 时, ;
③当 , 时, ;
④当 , 时, ;
⑤当 , 时, ;
⑥当 , 时, ;
则关于 与 之间数量关系的猜想是 .
(2)、请证明你的猜想;(3)、实践应用:要制作面积为1平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.