山东省聊城市高唐县2019-2020学年八年级下学期数学期中试卷
试卷更新日期:2021-04-14 类型:期中考试
一、单选题
-
1. 在-1.414, , ,3.14,2 ,3.212212221…这些数中,无理数的个数为( )
A、2 B、3 C、4 D、52. 一个正数的两个平方根分别是2a-1与-a+2,则a的值为( )A、1 B、-1 C、2 D、-23. 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别是a,b,c.若a=5,b=12,则c的长为( )A、 B、13 C、18 D、1694. 下列不等式变形正确的是( )A、由 得 B、由 得 C、由 得 D、由 得5. 下列二次根式中,不能与 合并的是( )A、 B、 C、 D、6. 下列命题是假命题的是( )A、对角线互相平分的四边形是平行四边形 B、对角线相等且互相平分的四边形是矩形 C、对角线互相垂直平分的四边形是菱形 D、对角线互相垂直的四边形是正方形7. 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( ) A、OE= DC B、OA=OC C、∠BOE=∠OBA D、∠OBE=∠OCE8. 如图,在Rt△PQR中,∠PRQ=90°,RP=RQ,边QR在数轴上.点Q表示的数为1,点R表示的数为3,以Q为圆心,QP的长为半径画弧交数轴负半轴于点P1 , 则P1表示的数是( )
A、OE= DC B、OA=OC C、∠BOE=∠OBA D、∠OBE=∠OCE8. 如图,在Rt△PQR中,∠PRQ=90°,RP=RQ,边QR在数轴上.点Q表示的数为1,点R表示的数为3,以Q为圆心,QP的长为半径画弧交数轴负半轴于点P1 , 则P1表示的数是( )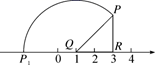 A、-2 B、-2 C、1-2 D、2 -19. 如图,将长方形纸片ABCD沿BD折叠,得到△ , 与AB交于点E,若∠1=35°,则∠2的度数为( )
A、-2 B、-2 C、1-2 D、2 -19. 如图,将长方形纸片ABCD沿BD折叠,得到△ , 与AB交于点E,若∠1=35°,则∠2的度数为( )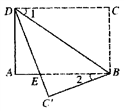 A、30° B、20° C、35° D、55°10. 如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2 , DE=2,则四边形 OCED 的面积为( )
A、30° B、20° C、35° D、55°10. 如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2 , DE=2,则四边形 OCED 的面积为( )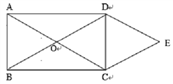 A、2 B、4 C、4 D、811. 关于x的不等式组 的解集为x<3,那么m的取值范围为( )A、m=3 B、m>3 C、m<3 D、m≥312. 如图,在矩形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )
A、2 B、4 C、4 D、811. 关于x的不等式组 的解集为x<3,那么m的取值范围为( )A、m=3 B、m>3 C、m<3 D、m≥312. 如图,在矩形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )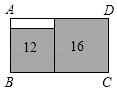 A、(8﹣4 )cm2 B、(4﹣2 )cm2 C、(16﹣8 )cm2 D、(﹣12+8 )cm2
A、(8﹣4 )cm2 B、(4﹣2 )cm2 C、(16﹣8 )cm2 D、(﹣12+8 )cm2二、填空题
-
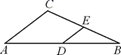
13. 若 有意义,则a的取值范围为14. 菱形的两条对角线分别是12和16,则此菱形的边长是 .15. 下列等式:① =±12,② =﹣2,③ =2,④ =- ,⑤ =﹣2;其中正确的有 . 只填序号)16. 如图,在△ABC中,点D,E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长等于 .
 17. 关于x的不等式组 无解,则m的取值范围是 .
17. 关于x的不等式组 无解,则m的取值范围是 .三、解答题
-
18. 已知2a﹣1的平方根是±3,3a﹣b﹣1的立方根是2,求a+b的算术平方根.19. 先化简,再求值:(1)、已知x=2+ ,y=2- ,求(x+y)(x-y)+y(x+2y)-(x-y)2的值;(2)、已知x= + ,y= - ,求x3y-xy3的值.20. 解下列不等式或不等式组:(1)、解不等式:5(x-2)+8<6(x-1)+7(2)、解不等式组: ,并把解集在数轴上表示出来.
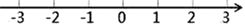 21. 如图,在RtΔABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,求EB′的长.
21. 如图,在RtΔABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,求EB′的长.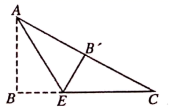 22. 已知:如图,点E为 中DC边的延长线上一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于点O,连接OF,猜想:AB与OF的关系,并证明你的结论.
22. 已知:如图,点E为 中DC边的延长线上一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于点O,连接OF,猜想:AB与OF的关系,并证明你的结论.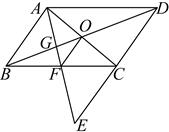 23. 小花家在装修客厅时,购进彩色地砖和原色地砖共120块,一共花费了8700元.已知原色地砖的价钱是60元/块,彩色地砖的价钱是110元/块.(1)、两种型号的地砖各采购了多少块?(2)、如果厨房也要铺这两种型号的地砖共70块,且采购费用不超过4400元,那么彩色地砖最多能采购多少块?24. 已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.
23. 小花家在装修客厅时,购进彩色地砖和原色地砖共120块,一共花费了8700元.已知原色地砖的价钱是60元/块,彩色地砖的价钱是110元/块.(1)、两种型号的地砖各采购了多少块?(2)、如果厨房也要铺这两种型号的地砖共70块,且采购费用不超过4400元,那么彩色地砖最多能采购多少块?24. 已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.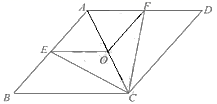 (1)、求证:△BCE≌△DCF;(2)、当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.25. 如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于点Q.
(1)、求证:△BCE≌△DCF;(2)、当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.25. 如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于点Q.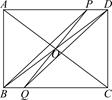 (1)、求证:四边形PBQD为平行四边形;(2)、若AB=3 cm,AD=4 cm,P从点A出发.以1 cm/s的速度向点D匀速运动.设点P运动时间为t s,问:四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由.
(1)、求证:四边形PBQD为平行四边形;(2)、若AB=3 cm,AD=4 cm,P从点A出发.以1 cm/s的速度向点D匀速运动.设点P运动时间为t s,问:四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由.