山东省济南市长清区2019-2020学年八年级下学期数学期中试卷

试卷更新日期：2021-04-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列代数式是分式的是（）

A、 $\frac{1}{2 - a}$ B、 $\frac{x - y}{2}$ C、 $\frac{x}{2}$ D、 $\frac{1}{π - 1}$

查看试题解析
2. 下列四个城市的地铁标志中，既是中心对称又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列各式从左到右的变形中，是因式分解的为（）

A、x（a+2b）＝ax+2bx B、x²﹣1+4y²＝（x﹣1）（x+1）+4y² C、x²﹣4y²＝（x+2y）（x﹣2y） D、ax+bx﹣c＝x（a+b）﹣c

查看试题解析
4. 已知一个多边形的内角和是540°，则这个多边形是（）

A、四边形 B、五边形 C、六边形 D、七边形

查看试题解析
5. 不等式组 ${\begin{matrix} 3 x - 1 > 2 \\ 2 - x \geq 0 \end{matrix}$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
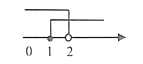6. 下列选项中，不能判定四边形ABCD是平行四边形的是 $($ 　　 $)$

A、 $AD / / BC$ ， $AB / / CD$ B、 $AB / / CD$ ， $AB = CD$ C、 $AD / / BC$ ， $AB = DC$ D、 $AB = DC$ ， $AD = BC$

查看试题解析
7. 下列各式中最简分式是 $($ $)$

A、 $\frac{12 a}{15 b}$ B、 $\frac{2 x}{6 x + 1}$ C、 $\frac{x + 1}{3 x + 3}$ D、 $\frac{5 a}{a}$

查看试题解析
8. 若关于 $x$ 的一元一次不等式组 ${\begin{array}{l} 1 - 2 x > x - 2 \\ x - a > 0 \end{array}$ 无解，则a的取值范围是（）

A、 $a > 1$ B、 $a \geq 1$ C、 $a \leq - 1$ D、 $a < - 1$

查看试题解析
9. 若分式 $\frac{x^{2} - 1}{x^{2} + x}$ 的值为0，则x的值是（）

A、1或-1 B、1 C、-1 D、0

查看试题解析
10. 如图，直线 $y = k x + 3$ 经过点(2，0)，则关于x的不等式 $k x + 3 \geq 0$ 的解集是（）

A、 $x > 2$ B、 $x < 2$ C、 $x \geq 2$ D、 $x \leq 2$

查看试题解析
11. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A'B'C ，连接AA'，若∠1=25°，则∠BAA'的度数是(　　)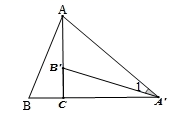

A、70° B、65° C、60° D、55°

查看试题解析
12. 如图，在Rt△ABC 中， $A B = A C$ ，D、E是斜边BC上两点，且∠DAE=45°，将△ $A D C$ 绕点 $A$ 顺时针旋转90 $°$ 后，得到△ $A F B$ ，连接 $E F$ .列结论：
①△ADC≌△AFB；②△ $A B E$ ≌△ $A C D$ ；③△ $A E D$ ≌△ $A E F$ ；④ $B E + D C = D E$
其中正确的是（）

A、②④ B、①④ C、②③ D、①③

查看试题解析

二、填空题

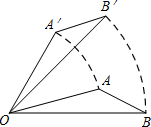
13. 用不等式表示：x与5的差不大于x的2倍：．

查看试题解析
14. 因式分解：2a²﹣8= ．

查看试题解析
15. △ABC中，D、E分别为AB、AC的中点，若DE＝4，AD＝3，AE＝2，则△ABC的周长为．

查看试题解析
16. 如图，将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′，若∠AOB＝15°，则∠AOB′的度数是．

查看试题解析
17. 小丽在化简分式 $\frac{*}{x^{2} - 1} = \frac{x - 1}{x + 1}$ 时，*部分不小心滴上了墨水，请你推测，*部分的代数式应该是．

查看试题解析
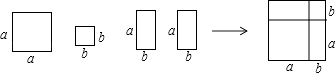
18.
利用1个a×a的正方形，1个b×b的正方形和2个a×b的矩形可拼成一个正方形（如图所示），从而可得到因式分解的公式．

查看试题解析

三、解答题

19. 因式分解：

(1)、 $a (x - y) - b (y - x)$ ；

(2)、 $3 a x^{2} + 6 a x y + 3 a y^{2}$

查看试题解析
20. 解分式方程： $\frac{1}{x - 2}$ = $\frac{3}{x}$

查看试题解析
21. 解不等式组： ${\begin{array}{l} 3 x - 2 < x + 4 \\ x + 1 > 4 x - 5 \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
22. 先化简，再求值： $(\frac{3 x}{x - 2} - \frac{x}{x + 2}) \cdot \frac{x^{2} - 4}{x}$ ，其中x＝1．

查看试题解析
23. 如图，平行四边形ABCD中，E、F分别是对角线BD上的两点，且BE＝DF，连接AE、AF、CE、CF．四边形AECF是什么样的四边形，说明你的道理．

查看试题解析
24. 如图，在平面直角坐标系中，Rt△ABC 的三个顶点分别是 A（﹣3，2），B（0，4），C（0，2）．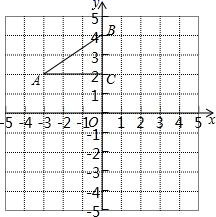

(1)、将△ABC 以点 O 为旋转中心旋转 180°，画出旋转后对应的△A₁B₁C₁；

(2)、平移△ABC，使对应点 A₂ 的坐标为（0，﹣4），写出平移后对应△A₂B₂C₂的中B₂ ， C₂点坐标．

查看试题解析
25. 为防控新冠肺炎，某药店用1000元购进若干医用防护口罩，很快售完，接着又用2500元购进第二批口罩，已知第二批所购口罩的数量是第一批所购口罩数的2倍，且每只口罩的进价比第一批的进价多 0.5元。求第一批口罩每只的进价是多少元？

查看试题解析
26. 某联通公司有甲、乙两种手机收费业务：甲种业务规定月租费10元，每通话1分钟收费0.3元；乙种业务不收月租费，但每通话1分钟收费0.4元．

(1)、分别写出甲、乙两种收费标准下每月应交费用y（元）与通话时间x分钟之间的关系式；

(2)、选择哪种业务对顾客更合算？

查看试题解析
27. 如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB的中点，点P为直线BC上的动点（不与点B点C重合），连接OC、OP，将线段OP绕点P顺时针旋转60°，得到线段PQ，连接BQ．

(1)、观察猜想：如图①，线段BQ与CP的数量关系是；∠CBQ＝；

(2)、探究证明：
如图②，当点P在CB的延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由．

查看试题解析