山东省济南市历城区2019-2020学年八年级下学期数学期中试卷
试卷更新日期:2021-04-14 类型:期中考试
一、单选题
-
1. 在以下四个标志图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 ,则下列结论错误的是( )A、 B、 C、 D、3. 如图,直线m∥n,点A在直线m上,点B、C在直线n上,AB=CB,∠1=70°,则∠BAC等于( )
2. 若 ,则下列结论错误的是( )A、 B、 C、 D、3. 如图,直线m∥n,点A在直线m上,点B、C在直线n上,AB=CB,∠1=70°,则∠BAC等于( )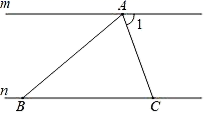 A、40° B、55° C、70° D、110°4. 下列等式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、5. 在数轴上表示不等式组 的解集,正确的是( )A、
A、40° B、55° C、70° D、110°4. 下列等式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、5. 在数轴上表示不等式组 的解集,正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,在平面直角坐标系中,已知点 ,点 ,平移线段AB,使点A落在点 处,则点B的对应点 的坐标为( )
6. 如图,在平面直角坐标系中,已知点 ,点 ,平移线段AB,使点A落在点 处,则点B的对应点 的坐标为( )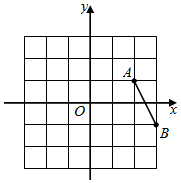 A、 B、 C、 D、7. 若a,b,c是三角形的三边,则代数式(a-b)2-c2的值是( )A、正数 B、负数 C、等于零 D、不能确定8. 如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径画弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
A、 B、 C、 D、7. 若a,b,c是三角形的三边,则代数式(a-b)2-c2的值是( )A、正数 B、负数 C、等于零 D、不能确定8. 如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径画弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( ) A、90° B、95° C、100° D、105°9. 如图,在△ABC中,∠BAC=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AD的长为( )
A、90° B、95° C、100° D、105°9. 如图,在△ABC中,∠BAC=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AD的长为( ) A、2 B、3 C、4 D、610. 如图,长和宽为a、b的长方形的周长为14,面积为10,则ab(a+b)的值为( )
A、2 B、3 C、4 D、610. 如图,长和宽为a、b的长方形的周长为14,面积为10,则ab(a+b)的值为( ) A、140 B、70 C、35 D、2411. 如图,在△ABC中,AB= ,AC= ,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( )
A、140 B、70 C、35 D、2411. 如图,在△ABC中,AB= ,AC= ,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( ) A、3 B、2 C、2 D、412. 如图,在 中, ,将 绕点A逆时针旋转 ,使点C落在点E处,点B落在点D处,则 两点间的距离为( )
A、3 B、2 C、2 D、412. 如图,在 中, ,将 绕点A逆时针旋转 ,使点C落在点E处,点B落在点D处,则 两点间的距离为( )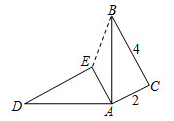 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 因式分解:a2-9=.14. 若 ,则ab(填“<、>或=”号).15. 如图,在△ABC中,∠C=90°,AD平分∠CAB,AD=5,AC=4,则D点到AB的距离是 .
 16. 如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式kx+6>x+b的解集是 .
16. 如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式kx+6>x+b的解集是 . 17. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A'B'C',连接A'C,则线段A'C的长为 .
17. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A'B'C',连接A'C,则线段A'C的长为 . 18. 如图, 度, , ,且 ,AF平分 交BC于F,若 , ,则线段AD的长为 .
18. 如图, 度, , ,且 ,AF平分 交BC于F,若 , ,则线段AD的长为 .
三、解答题
-
19. 分解因式:(1)、(2)、20. 解不等式: ≥ ,并把它的解集在数轴上表示出来.
 21. 解不等式组 ,并把不等式组的解集在数轴上表示出来.
21. 解不等式组 ,并把不等式组的解集在数轴上表示出来.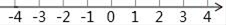 22. 解不等式组: 并写出满足条件的所有整数x的值.23. 已知:如图,在 中, ,垂足为点 , ,垂足为点 ,且 .
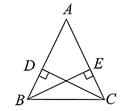
22. 解不等式组: 并写出满足条件的所有整数x的值.23. 已知:如图,在 中, ,垂足为点 , ,垂足为点 ,且 .求证: .
 24. 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
24. 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形). (1)、将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;(2)、将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;(3)、直接写出点B2 , C2的坐标.25. 今年 3 月 12 日植树节期间, 学校预购进 A、B 两种树苗,若购进 A种树苗 3 棵,B 种树苗 5 棵,需 2100 元,若购进 A 种树苗 4 棵,B 种树苗 10棵,需 3800 元.(1)、求购进 A、B 两种树苗的单价;(2)、若该单位准备用不多于 8000 元的钱购进这两种树苗共 30 棵,求 A 种树苗至少需购进多少棵?26. 如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=8cm.点D从点C开始沿射线CB方向以每秒2厘米的速度运动,连结AD,设运动时间为t秒.
(1)、将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;(2)、将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;(3)、直接写出点B2 , C2的坐标.25. 今年 3 月 12 日植树节期间, 学校预购进 A、B 两种树苗,若购进 A种树苗 3 棵,B 种树苗 5 棵,需 2100 元,若购进 A 种树苗 4 棵,B 种树苗 10棵,需 3800 元.(1)、求购进 A、B 两种树苗的单价;(2)、若该单位准备用不多于 8000 元的钱购进这两种树苗共 30 棵,求 A 种树苗至少需购进多少棵?26. 如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=8cm.点D从点C开始沿射线CB方向以每秒2厘米的速度运动,连结AD,设运动时间为t秒. (1)、求AB的长.(2)、当t为多少时,△ABD为等腰三角形.27. 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=6,D在线段BC上,E是线段AD的一点.现以CE为直角边,C为直角顶点,在CE的下方作等腰直角△ECF , 连接BF .
(1)、求AB的长.(2)、当t为多少时,△ABD为等腰三角形.27. 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=6,D在线段BC上,E是线段AD的一点.现以CE为直角边,C为直角顶点,在CE的下方作等腰直角△ECF , 连接BF .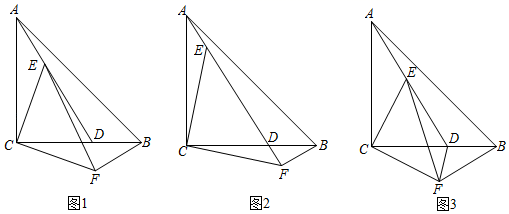 (1)、如图1,求证:AE=BF;(2)、当A、E、F三点共线时,如图2,若BF=2,求AF的长;(3)、如图3,若∠BAD=15°,连接DF , 当E运动到使得∠ACE=30°时,求△DEF的面积.
(1)、如图1,求证:AE=BF;(2)、当A、E、F三点共线时,如图2,若BF=2,求AF的长;(3)、如图3,若∠BAD=15°,连接DF , 当E运动到使得∠ACE=30°时,求△DEF的面积.