江西省萍乡市安源区2019-2020学年八年级下学期数学期中试卷
试卷更新日期:2021-04-14 类型:期中考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知等腰三角形的一边长为2,周长为8,那么它的腰长为 ( )A、2 B、3 C、2或3 D、不能确定3. 如图,在△ABC中,AB=AD=DC,∠BAD=26°,则∠C的度数是( )
2. 已知等腰三角形的一边长为2,周长为8,那么它的腰长为 ( )A、2 B、3 C、2或3 D、不能确定3. 如图,在△ABC中,AB=AD=DC,∠BAD=26°,则∠C的度数是( ) A、36° B、77° C、64° D、38.5°4. 如图,在 中, ,沿 折叠 ,使点 恰好落在边 上点 处,若 ,则 的大小为( )
A、36° B、77° C、64° D、38.5°4. 如图,在 中, ,沿 折叠 ,使点 恰好落在边 上点 处,若 ,则 的大小为( ) A、 B、 C、 D、5. 已知不等式组 有解,则a的取值范围为( )A、a>﹣2 B、a≥﹣2 C、a<2 D、a≥26. 不等式组 的解集在数轴上可以表示为( )。A、
A、 B、 C、 D、5. 已知不等式组 有解,则a的取值范围为( )A、a>﹣2 B、a≥﹣2 C、a<2 D、a≥26. 不等式组 的解集在数轴上可以表示为( )。A、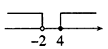 B、
B、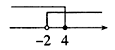 C、
C、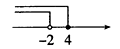 D、
D、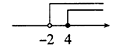 7. 用反证法证明:“一个三角形中,至少有一个内角大于或等于60°”.应假设( )A、一个三角形中没有一个内角大于或等于60° B、一个三角形中至少有一个内角小于60° C、一个三角形中三个内角都大于或等于60° D、一个三角形中有一个内角大于或等于60°8. 如图,一次函数y=kx+b(k、b为常数,且k≠0)与正比例函数y=ax(a为常数,且a≠0)相交于点P,则不等式kx+b<ax的解集是( )
7. 用反证法证明:“一个三角形中,至少有一个内角大于或等于60°”.应假设( )A、一个三角形中没有一个内角大于或等于60° B、一个三角形中至少有一个内角小于60° C、一个三角形中三个内角都大于或等于60° D、一个三角形中有一个内角大于或等于60°8. 如图,一次函数y=kx+b(k、b为常数,且k≠0)与正比例函数y=ax(a为常数,且a≠0)相交于点P,则不等式kx+b<ax的解集是( ) A、x>1 B、x<1 C、x>2 D、x<2
A、x>1 B、x<1 C、x>2 D、x<2二、填空题
-
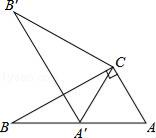
9. 三角形的两边长分别是3和7,则其第三边x的范围为 .10. 命题“全等三角形的面积相等”的逆命题是11. 不等式 的负整数解为 .12. 已知 , ,则2x3y+4x2y2+2xy3=.13. 等腰三角形腰上的高与腰的夹角为47°,则这个三角形的顶角为度.14. 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为 .
 15. 如图,在△ABC中,∠B=30°,ED垂直平分BC , ED=3.则CE的长为 .
15. 如图,在△ABC中,∠B=30°,ED垂直平分BC , ED=3.则CE的长为 .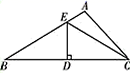 16. 如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为 .
16. 如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为 .
三、解答题
-
17. 分解因式:(a2+1)2-4a218. 解不等式组,并把解集在数轴上表示出来:19. 用圆规、直尺作图,不写作法,但要保留作图痕迹.
已知:四边形ABCD
求作:点P,使∠PBC=∠PCB,且点P到AD和DC的距离相等.
 20. 小丽准备用35元买牛奶和面包,已知一盒牛奶3.5元,一个面包5元,她买了4盒牛奶,她最多还能买多少个面包.21. 在保护地球爱护家园活动中,校团委把一批树苗分给初三(1)班同学去栽种.如果每人分2棵,还剩42棵;如果前面每人分3棵,那么最后一人得到的树苗少于5棵(但至少分得一棵).那么初三(1)班至少有多少名同学?最多有多少名同学?22. 如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O
20. 小丽准备用35元买牛奶和面包,已知一盒牛奶3.5元,一个面包5元,她买了4盒牛奶,她最多还能买多少个面包.21. 在保护地球爱护家园活动中,校团委把一批树苗分给初三(1)班同学去栽种.如果每人分2棵,还剩42棵;如果前面每人分3棵,那么最后一人得到的树苗少于5棵(但至少分得一棵).那么初三(1)班至少有多少名同学?最多有多少名同学?22. 如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O (1)、求证:OB=OC;(2)、若∠ABC=50°,求∠BOC的度数.
(1)、求证:OB=OC;(2)、若∠ABC=50°,求∠BOC的度数.
