初中数学浙教版2020-2021学年七年级下学期数学期中模拟试卷（2）

试卷更新日期：2021-04-13 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示，△DEF经过平移可以得到△ABC，那么∠C的对应角和ED的对应边分别是（）

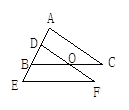A、∠F，AC B、∠BOD，BA C、∠F，BA D、∠BOD，AC

查看试题解析
2. 下列方程中，是二元一次方程的是（　　）

A、xy＝2 B、3x＝4y C、x+ $\frac{1}{y}$ ＝2 D、x²+2y＝4

查看试题解析
3. 计算 $y^{2} \cdot (- 2 x y)$ 的结果是（）

A、 $- 2 x y^{3}$ B、 $2 x^{2} y^{3}$ C、 $- 2 x^{2} y^{3}$ D、 $2 x y^{3}$

查看试题解析
4. 如图，下列四个角中，与∠1构成一对同位角的是（）

A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
5. 已知 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$ 是方程mx-y=2的解，则m的值是（）

A、 $- 1$ B、 $- \frac{1}{3}$ C、1 D、5

查看试题解析
6. 计算 ${(- \frac{2}{3})}^{2018} \times {(1.5)}^{2019}$ 的结果是（）

A、 $- \frac{2}{3}$ B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、 $- \frac{3}{2}$

查看试题解析
7. 如图，给出下列条件：①∠1＝∠2：②∠3＝∠4：③AB∥CE，且∠ADC＝∠B：④AB∥CE，且∠BCD＝∠BAD.其中能推出BC∥AD的条件为（）

A、①② B、②④ C、②③ D、②③④

查看试题解析
8. 下列各式不能用平方差公式计算的是（）

A、（2a－3b）（3a＋2b） B、（4a² －3bc）（ 4a² ＋3bc） C、（3a＋2b）（2b－3a） D、（3m＋5）（5－3m）

查看试题解析
9. 下列因式分解正确的是（）

A、m²+n²=(m+n)(m-n) B、a³-a=a(a+1)(a-1) C、a²-2a+1=a(a-2)+1 D、x²+2x-1=(x-1)²

查看试题解析
10. 如图，将长方形ABCD的各边向外作正方形，若四个正方形周长之和为24，面积之和为6，则长方形ABCD的面积为（）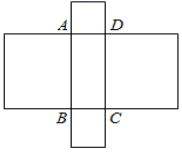

A、4 B、3 C、5 D、6

查看试题解析

二、填空题

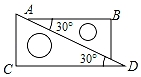
11. 若方程2x^2a^＋^b^－⁴＋4y^3a^－^2b^－³＝1是关于x，y的二元一次方程，则a＝， b＝.

查看试题解析
12. 如图，将两个含30°角的直角三角板的最长边靠在一起滑动，可知直角边AB∥CD，依据是.

查看试题解析
13. 设 $M = x + y$ ， $N = x - y$ ， $P = x y$ .若 $M = 1$ ， $N = 2$ ，则 $P =$ .

查看试题解析
14. 计算： $(1 - 2 y) (2 y + 1) =$ ．

查看试题解析
15. 如图，a//b，点B在直线b上，且AB⊥BC，∠1=35°，那么∠2=.

查看试题解析
16. 如图，AB∥CD，AB⊥AE，∠CAE＝42°，则∠ACD的度数为.

查看试题解析

三、解答题

17. 关于x、y的二元一次方程组 ${\begin{matrix} a x + b y = 2 \\ a x - b y = 4 \end{matrix}$ 与 ${\begin{matrix} 2 x - 3 y = 4 \\ 4 x - 5 y = 6 \end{matrix}$ 的解相同，求a、b的值.

查看试题解析
18. 先化简，再求值：
$\frac{1}{2} x - 2 (x - \frac{1}{3} y^{2}) + (- \frac{3}{2} x + \frac{1}{3} y^{2})$ ，其中： $x = - 2$ ， $y = \frac{1}{2}$

查看试题解析
19. 一名34岁的男子带着他的两个孩子一同进行晨跑，下面是两个孩子与记者的对话：

根据对话内容，请你用方程的知识帮记者求出哥哥和妹妹的年龄.

查看试题解析
20. 综合题。

(1)、计算： $| - 3 | + \sqrt{16} + \frac{1}{2} \times \sqrt[3]{- 8}$

(2)、解方程组： ${\begin{cases} 2 x + 3 y = 22 \\ x - y = 6 \end{cases}$

查看试题解析
21. 计算
（1） $- 2^{2} + {(- \frac{1}{2})}^{- 1} + {(3 - π)}^{0}$
（2）（﹣a）²•a⁴÷a³
（3）（2x﹣1）（x﹣3）
（4）（3x﹣2y）²（3x+2y）²
（5）（x﹣2y+4）（x﹣2y﹣4）

查看试题解析
22. 完成下面推理过程．如图：已知 $∠ 1 = ∠ 2$ ， $∠ A = ∠ D$ ．求证： $∠ B = ∠ C$ ．

证明： $∵ ∠ 1 = ∠ 2$ （已知）

$∵ ∠ 1 = ∠ 3$ （   ▲   ）

$∴ ∠ 2 = ∠$ （   ▲   ）（等量代换）

$∴ A E // F D$ （同位角相等，两直线平行）

$∴ ∠ A = ∠$ （   ▲   ）（   ▲   ）

$∴ ∠ A = ∠ D$ （已知）

$∴ ∠ D = ∠ B F D$ （等量代换）

$∴$ （   ▲   ） $// C D$ （   ▲   ）

$∴ ∠ B = ∠ C$ （两直线平行，内错角相等）

查看试题解析
23. 在计算 $(x + a) (x + b)$ 时，甲把错 $b$ 看成了6，得到结果是： $x^{2} + 8 x + 12$ ；乙错把 $a$ 看成了 $- a$ ，得到结果： $x^{2} + x - 6$ .

(1)、求出 $a, b$ 的值；

(2)、在（1）的条件下，计算 $(x + a) (x + b)$ 的结果.

查看试题解析
24. 如图

(1)、如图1，已知正方形ABCD的边长为a，正方形FGCH的边长为b，长方形ABGE和EFHD为阴影部分，则阴影部分的面积是（写成平方差的形式）

(2)、将图1中的长方形ABGE和EFHD剪下来，拼成图2所示的长方形，则长方形AHDE的面积是（写成多项式相乘的形式）

(3)、比较图1与图2的阴影部分的面积，可得乘法公式.

(4)、利用所得公式计算：2（1+ $\frac{1}{2}$ ）（1+ $\frac{1}{2^{2}}$ ）（1+ $\frac{1}{2^{4}}$ ）（1+ $\frac{1}{2^{8}}$ ）+ $\frac{1}{2^{14}}$ .

查看试题解析