四川省成都市青羊区石室2020-2021学年七年级下学期数学开学试卷
试卷更新日期:2021-04-13 类型:开学考试
一、选择题(本大题共10个小题,每小题3分,共30分)
-
1. ﹣ 的倒数是( )A、 B、 C、﹣ D、﹣2. 单项式﹣2xy3的次数是( )A、2 B、3 C、4 D、53. 下面四个几何体中,俯视图为四边形的是( )A、
 B、
B、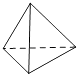 C、
C、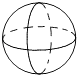 D、
D、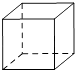 4. 下列方程中是一元一次方程的是( )A、x﹣1=2x B、 =2 C、x+3=y+2 D、x2﹣1=05. 如图, 是北偏东30°方向的一条射线,若射线 与射线 垂直.则 的方向角是( )
4. 下列方程中是一元一次方程的是( )A、x﹣1=2x B、 =2 C、x+3=y+2 D、x2﹣1=05. 如图, 是北偏东30°方向的一条射线,若射线 与射线 垂直.则 的方向角是( )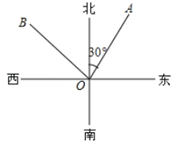 A、北偏西30° B、北偏西60° C、东偏北30° D、东偏北60°6. 下列调查方式合适的是( )A、为了了解市民对电影《南京》的感受,小华在某校随机采访了8名初三学生 B、为了了解全校学生用于做数学作业的时间,小民同学在网上向3位好友做了调查 C、为了了解“嫦娥一号”卫星零部件的状况,检测人员采用了普查的方式 D、为了了解全国青少年儿童的睡眠时间,统计人员采用了普查的方式7. 下列计算正确的是( )A、x2y﹣2x2y=﹣x2y B、x2+x3=x5 C、2(x+2y)=2x+2y D、7xy﹣xy=78. 下列说法正确的个数为( )
A、北偏西30° B、北偏西60° C、东偏北30° D、东偏北60°6. 下列调查方式合适的是( )A、为了了解市民对电影《南京》的感受,小华在某校随机采访了8名初三学生 B、为了了解全校学生用于做数学作业的时间,小民同学在网上向3位好友做了调查 C、为了了解“嫦娥一号”卫星零部件的状况,检测人员采用了普查的方式 D、为了了解全国青少年儿童的睡眠时间,统计人员采用了普查的方式7. 下列计算正确的是( )A、x2y﹣2x2y=﹣x2y B、x2+x3=x5 C、2(x+2y)=2x+2y D、7xy﹣xy=78. 下列说法正确的个数为( )(1)过两点有且只有一条直线
(2)连接两点的线段叫做两点间的距离
(3)两点之间的所有连线中,线段最短
(4)直线AB和直线BA表示同一条直线.
A、1 B、2 C、3 D、49. 如果A,B,C三点同在一直线上,且线段AB=6cm,BC=3cm,A,C两点的距离为d,那么d=( )A、9cm B、3cm C、9cm或3cm D、大小不定10. 如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED'=50°,则∠EFC等于( )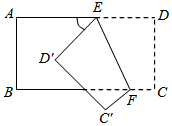 A、65° B、110° C、115° D、130°
A、65° B、110° C、115° D、130°二、填空题(本大题共5个小题,每小题4分,共20分)
-
11. 根据成都市城市轨道交通第三期的建设规划(2016~2020年),至2020年,我市将形成13条线路,总长508000米的轨道交通网,将508000用科学记数法表示为.12. 已知∠α=67°32',则∠α的的补角等于.13. 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是.
 14. 如果|m﹣3|+(n+2)2=0,那么﹣5xmy﹣n+7x3y2=.15. 钟面上 8 点 30 分时,时针与分针的夹角的度数是 .
14. 如果|m﹣3|+(n+2)2=0,那么﹣5xmy﹣n+7x3y2=.15. 钟面上 8 点 30 分时,时针与分针的夹角的度数是 .三、解答题(本大题共6个小题,共50分)
-
16.(1)、计算:3+ ;(2)、(﹣2)3﹣ ;(3)、化简:﹣4(a3﹣3b)+(﹣2b+5a3);(4)、解方程: ;(5)、(3x+2)(3x﹣2)﹣5x(x+1).17. 先化简,再求值: ,其中 .18. 已知如图,BC∥EF,∠AOB=80°,∠1+∠C=160°,∠B=60°,求证:∠A=∠D.
完成下面的证明过程:

证明:∵∠AOB=80°,
∴∠COD=∠AOB=80°( ).
∵▲(已知),
∴∠COD+∠1=180°( ).
∴∠1=100°.
∵∠1+∠C=160°(已知),
∴∠C=160°﹣∠1=▲ .
又∵∠B=60°,
∴∠B=∠C.
∴AB∥CD( ).
∴∠A=∠D( ).
19. 某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计,并绘制如图所示的扇形统计图和条形统计图.根据图中信息解答下列问题: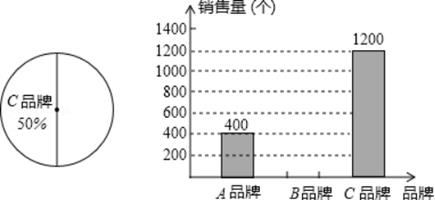 (1)、该超市“元旦”期间共销售个绿色鸡蛋,A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是度;(2)、补全条形统计图;(3)、如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个,请你估计这个分店销售的B种品牌的绿色鸡蛋的个数?20. 已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.
(1)、该超市“元旦”期间共销售个绿色鸡蛋,A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是度;(2)、补全条形统计图;(3)、如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个,请你估计这个分店销售的B种品牌的绿色鸡蛋的个数?20. 已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.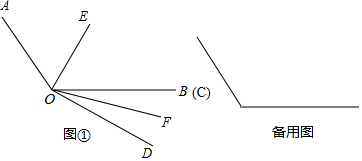 (1)、如图①,当OB、OC重合时,求∠AOE﹣∠BOF的值;(2)、当∠COD从图①所示位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.
(1)、如图①,当OB、OC重合时,求∠AOE﹣∠BOF的值;(2)、当∠COD从图①所示位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.四、填空题(本大题共5个小题,每小题4分,共20分)
-
21. 若xm=2,xn=5,则xm+n= .22. 已知如图,AB∥CD,∠A=130°,∠D=25°,那么∠AED=°.
 23. 已知a、b、c在数轴上的对应点如图所示,化简|a+c|﹣|a+b|+2|c﹣b|=.
23. 已知a、b、c在数轴上的对应点如图所示,化简|a+c|﹣|a+b|+2|c﹣b|=. 24. 一个长方体水箱,从里面量长、宽、高分别为40cm、30cm和30cm,箱中水面高10cm,放进一个棱长为20cm的正方体铁块后,这时水面高为cm.25. 如图,将从1开始的正整数按规律排列,例如:位于第3行、第4列的数是12,则位于第45行、第6列的数是 .
24. 一个长方体水箱,从里面量长、宽、高分别为40cm、30cm和30cm,箱中水面高10cm,放进一个棱长为20cm的正方体铁块后,这时水面高为cm.25. 如图,将从1开始的正整数按规律排列,例如:位于第3行、第4列的数是12,则位于第45行、第6列的数是 .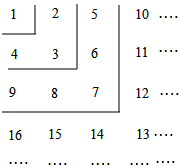
五、解答题(本大题共3个小题,共30分)
-
26.(1)、已知代数式A=2a2+3ab+2b﹣1,B=a2﹣ab+a﹣ .若A﹣2B的值与a的取值无关,求b的值.(2)、已知关于x的方程 ﹣x=﹣a的解是关于x的方程 = x﹣a的解的三分之一.求a的值.27. 某超市第一次用6200元购进了甲、乙两种商品,其中乙种商品的件数比甲种商品的件数的4倍少40件,甲、乙两种商品的进价和售价如表:(注:获利=售价﹣进价)
甲
乙
进价(元/件)
20
25
售价(元/件)
25
35
(1)、该超市第一次购进甲、乙两种商品各多少件?(2)、该超市将第一次购进的甲、乙两种商品全部销售完后一共可获得多少利润?(3)、该超市第二次以第一次的进价又购进甲、乙两种商品.其中甲种商品的件数不变,乙种商品的件数是第一次的2倍;甲种商品按原售价提价a%销售,乙种商品按原售价降价a%销售,如果第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多1000元,那么a的值是多少.28. 已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD. (1)、若∠O=50°,求∠BCD的度数;(2)、求证:CE平分∠OCA;(3)、当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.
(1)、若∠O=50°,求∠BCD的度数;(2)、求证:CE平分∠OCA;(3)、当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.