浙江省绍兴市柯桥区联盟校2021届九年级下学期数学3月月考试卷
试卷更新日期:2021-04-13 类型:月考试卷
一、选择题(本大题有10小题,每小题4分,共40分)
-
1. =( )A、3 B、-3 C、 D、2. 数据1800000用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 测试五位学生“一分钟跳绳”成绩,得到五个各不相同的数据,统计时,出现了一处错误:将最高成绩写得更高了。计算结果不受影响的是( )
A、方差 B、标准差 C、中位数 D、平均数5. 若线段 , 分别是 边上的高线和中线,则( )A、 B、 C、 D、6. 用配方法解方程x2﹣6x﹣8=0时,配方结果正确的是( )A、(x﹣3)2=17 B、(x﹣3)2=14 C、(x﹣6)2=44 D、(x﹣3)2=17. 如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α , ∠ADC=β , 则竹竿AB与AD的长度之比为( )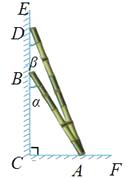 A、 B、 C、 D、8. 如图,将△ABC绕点C顺时针旋转90°得到△EDC . 若点A , D , E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A、 B、 C、 D、8. 如图,将△ABC绕点C顺时针旋转90°得到△EDC . 若点A , D , E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )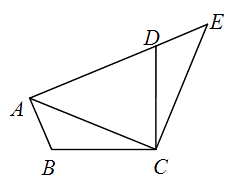 A、55° B、60° C、65° D、70°9. 四位同学在研究函数 (b,c是常数)时,甲发现当 时,函数有最小值;乙发现 是方程 的一个根;丙发现函数的最小值为3;丁发现当 时, .已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A、55° B、60° C、65° D、70°9. 四位同学在研究函数 (b,c是常数)时,甲发现当 时,函数有最小值;乙发现 是方程 的一个根;丙发现函数的最小值为3;丁发现当 时, .已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A、甲 B、乙 C、丙 D、丁10. 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )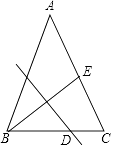 A、x﹣y2=3 B、2x﹣y2=9 C、3x﹣y2=15 D、4x﹣y2=21
A、x﹣y2=3 B、2x﹣y2=9 C、3x﹣y2=15 D、4x﹣y2=21二、填空题(本大题有6小题,每小题5分,共30分)
-
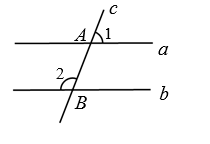
11. 化简 的结果是 .12. 如图,直线 ,直线 与直线 分别交于A,B,若 ,则 。
 13. 对于两个非零实数x , y , 定义一种新的运算: .若 ,则 的值是 .14. 如图,AB是⊙的直径,点C是半径OA的中点,过点C作 ,交O于点D、E两点,过点D作直径DF,连结AF,则
13. 对于两个非零实数x , y , 定义一种新的运算: .若 ,则 的值是 .14. 如图,AB是⊙的直径,点C是半径OA的中点,过点C作 ,交O于点D、E两点,过点D作直径DF,连结AF,则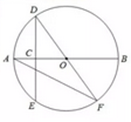 15. 如图2,小靓用七巧板拼成一幅装饰图,放入长方形ABCD内,装饰图中的三角形顶点E , F分别在边AB , BC上,三角形①的边GD在边AD上,则 的值是 .
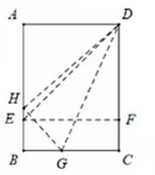
15. 如图2,小靓用七巧板拼成一幅装饰图,放入长方形ABCD内,装饰图中的三角形顶点E , F分别在边AB , BC上,三角形①的边GD在边AD上,则 的值是 .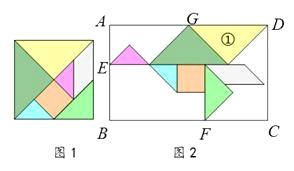 16. 折叠矩形纸片ABCD时,发现可以进行如下操作:①把 翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把 翻折,点C落在直线AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,
16. 折叠矩形纸片ABCD时,发现可以进行如下操作:①把 翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把 翻折,点C落在直线AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=
三、解答题:(本大题有8小题,第17~20小题每小题8分,第21小题10分,第22,23小题每小题12分,第24小题14分,共80分.)
-
17.(1)、计算:(2)、解不等式组:18. 在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).(1)、当﹣2<x≤3时,求y的取值范围;(2)、已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.19. 为了解朝阳社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
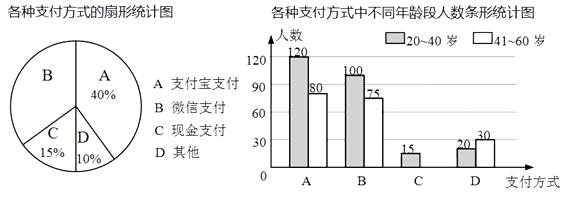 (1)、求参与问卷调查的总人数.(2)、补全条形统计图.(3)、该社区中20-60岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.20. 如图,将一个直角三角形形状的楔子(Rt△ABC)从木桩的底端点P沿水平方向打入木桩底,可以使木桩向上运动.如果楔子底面的倾斜角为10°,其高度AC为1.8厘米,楔子沿水平方向前进一段距离(如箭头所示),留在外面的楔子长度HC为3厘米.
(1)、求参与问卷调查的总人数.(2)、补全条形统计图.(3)、该社区中20-60岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.20. 如图,将一个直角三角形形状的楔子(Rt△ABC)从木桩的底端点P沿水平方向打入木桩底,可以使木桩向上运动.如果楔子底面的倾斜角为10°,其高度AC为1.8厘米,楔子沿水平方向前进一段距离(如箭头所示),留在外面的楔子长度HC为3厘米.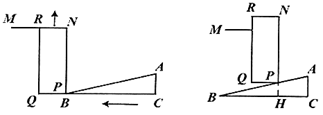
(sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,结果精确到0.1厘米)
(1)、求BH的长;(2)、木桩上升了多少厘米?21. 某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:销售单价x(元/千克)
55
60
65
70
销售量y(千克)
70
60
50
40
(1)、求y(千克)与x(元/千克)之间的函数表达式;(2)、为保证某天获得600元的销售利润,则该天的销售单价应定为多少?(3)、当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?22. 如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.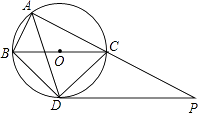 (1)、求证:PD是⊙O的切线;
(1)、求证:PD是⊙O的切线;
(2)、求证:△ABD∽△DCP;
(3)、当AB=5cm,AC=12cm时,求线段PC的长.
23. 已知抛物线y=ax2+bx+c经过A(2,0),B(3n﹣4,y1),C(5n+6,y2)三点,对称轴是直线x=1.关于x的方程ax2+bx+c=x有两个相等的实数根.(1)、求抛物线的解析式;(2)、若n<﹣5,试比较y1与y2的大小;(3)、若B,C两点在直线x=1的两侧,且y1>y2 , 求n的取值范围.24. 有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.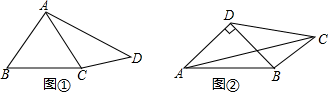 (1)、【理解运用】
(1)、【理解运用】
如图①,对余四边形ABCD中,AB=5,BC=6,CD=4,连接AC.若AC=AB,求sin∠CAD的值;(2)、如图②,凸四边形ABCD中,AD=BD,AD⊥BD,当2CD2+CB2=CA2时,判断四边形ABCD是否为对余四边形.证明你的结论;(3)、【拓展提升】在平面直角坐标系中,点A(﹣1,0),B(3,0),C(1,2),四边形ABCD是对余四边形,点E在对余线BD上,且位于△ABC内部,∠AEC=90°+∠ABC.设 =u,点D的纵坐标为t,请直接写出u关于t的函数解析式.