浙江省绍兴市柯桥区联盟校2020-2021学年八年级下学期数学3月月考试卷

试卷更新日期：2021-04-13 类型：月考试卷

进入出卷网下载

一、选择题（本大题有10小题，每小题2分，共20分）

1. 下列方程中为一元二次方程的是（）

A、 $x^{2} = 1$ B、 $(x + 2) (x - 1) = x^{2}$ C、 $10 y = 4 x^{2}$ D、 $x {}^{2}+ \frac{1}{x} = 3$

查看试题解析
2. 数据10，10，10，11，12，12，13，13的众数是（）

A、10 B、11 C、12 D、13

查看试题解析
3. 下列各式中能与合并的二次根式的是（）.

A、 $\sqrt{6}$ B、 C、 D、

查看试题解析
4. 若关于x的一元二次方程 $(a - 1) x^{2} + x + a^{2} - 1 = 0$ 的一个根是0，则 $a$ 的值是（）

A、1 B、－1 C、1或－1 D、0

查看试题解析
5. 小林在计算时遇到以下情况，结果正确的是（）

A、 $\sqrt{5^{2} + 12^{2}} = \sqrt{5^{2}} + \sqrt{12^{2}} = 5 + 12 = 17$ B、 $\sqrt{{(\sqrt{3} - 2)}^{2}} = \sqrt{3} - 2$ C、 ${(- \sqrt{4 \frac{2}{3}})}^{2} = \sqrt{{(- 4 \frac{2}{3})}^{2}}$ D、 $\sqrt{1 - \frac{1}{16}} = 1 - \frac{1}{4} = \frac{3}{4}$

查看试题解析
6. 在四边形ABCD中，∠A+∠C=180°，∠B比∠D大60°，则∠B的度数为（）

A、60° B、80° C、120° D、130°

查看试题解析
7. 已知方程x²－6x + q = 0可以配方成（x－p）² =7的形式，那么x²－6x +q =2可以配方成下列的（）

A、（x－p）² =9 B、（x－p）² = 5 C、（x－p +2）² =9 D、（x－p + 2）² =5

查看试题解析
8. 根据下列表格的对应值：

x

0.59

0.60

0.61

0.62

0.63

x²+x-1

-0.061

-0.04

-0.017

0.0044

0.0269

判断方程x²+x-1=0一个解的取值范围是（）

A、0.59<x<0.61 B、0.60<x<0.61 C、0.61<x<0.62 D、0.62<x<0.63

查看试题解析
9. 若t是方程 $a x^{2} + 2 x + c = 0$ (a≠0)的一个根，设P＝1－ac，Q＝(at＋1)² ，则P与Q的大小关系正确的是（）

A、P<Q B、P＝Q C、P>Q D、不确定

查看试题解析
10. 如图是按一定规律排成的三角形数阵，按图中数阵的排列规律，第10行从左至右第6个数是（　　）

A、2 $\sqrt{10}$ B、 $\sqrt{41}$ C、5 $\sqrt{2}$ D、 $\sqrt{51}$

查看试题解析

二、填空题（本大题有10小题，每小题3分，共30分）

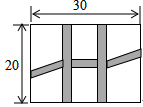
11. 一个多边形的每个外角都是36°，则这个多边形的内角和等于度.

查看试题解析
12. 某少年军校准备从甲，乙，丙三位同学中选拔一人参加全市射击比赛，他们在选拔比赛中，射靶十次的平均环数是 ${\bar{x}}_{甲}$ = ${\bar{x}}_{乙}$ ＝ ${\bar{x}}_{丙}$ =8.3，方差分别是 $S_{甲}^{2}$ =1.5， $S_{乙}^{2}$ =2.8， $S_{丙}^{2}$ =3.2.那么，根据以上提供的信息，你认为应该推荐参加全市射击比赛的同学是 .

查看试题解析
13. 若一元二次方程（k﹣1）x²﹣2x+1＝0有实数根，则实数k的取值范围

查看试题解析
14. 某超市一月份的营业额200万元，一月、二月、三月的营业额共1000万元，如果平均每月增长率为x，则由题意列方程为

查看试题解析
15. 如图，是一个长为30m，宽为20m的矩形花园，现要在花园中修建等宽的小道，剩余的地方种植花草．如图所示，要使种植花草的面积为532m² ，那么小道进出口的宽度应为米．

查看试题解析
16. 已知在数轴上的位置如图所示，化简：

$\sqrt{n^{2}} + \sqrt{{(m - n)}^{2}} + \sqrt{{(m + 1)}^{2}}$ =.

查看试题解析
17. 如图，正三角形和矩形具有一条公共边，矩形内有一个正方形，其四个顶点都在矩形的边上，正三角形和正方形的面积分别是2 $\sqrt{3}$ 和2，则图中阴影部分的面积是．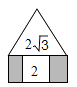

查看试题解析
18. 如图，在△ABC中， ∠B = 90°，点P从点 A 开始沿AB边向点B以 1cm / s 的速度移动， Q 从点B开始沿 BC 边向C点以 2 cm / s 的速度移动，如果点P、Q分别从A、B同时出发，秒钟后， △PBQ 的面积等于8 cm².

查看试题解析
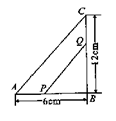19. 如果m 、n 是两个不相等的实数，且满足m²-m=3，n²-n=3，那么代数式 $2 n {}^{2}- mn + 2 m + 2021$ =

查看试题解析
20. 已知图②是由图①七巧板拼成的数字“0”，若正方形ABCD的边长为 $12 \sqrt{2}$ ，则六边形EFGHMN的周长为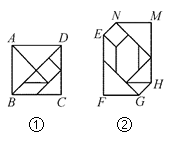

查看试题解析

三、解答题（本大题有7小题，共50分，解答需写出必要的文字说明、演算步骤或过程）

21. 化简：

(1)、 $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} - \sqrt{24}$

(2)、 ${(3 \sqrt{5} + 5 \sqrt{3})}^{2} - {(3 \sqrt{5} - 5 \sqrt{3})}^{2}$

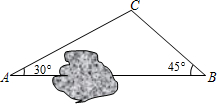
查看试题解析
22. 解方程：

(1)、x²－6x－9＝0；

(2)、 $9 {(2 x + 3)}^{2} = 16 {(1 - 3 x)}^{2}$

查看试题解析
23.
如图，A、B两地之间有一座山，汽车原来从A地到B地经过C地沿折线A→C→B行驶，现开通隧道后，汽车直接沿直线AB行驶．已知AC=10千米，∠A=30°，∠B=45°．则隧道开通后，汽车从A地到B地比原来少走多少千米？（结果保留根号）

查看试题解析
24. 为了倡导“节约用水，从我做起”，市政府决定对某小区500户家庭的用水情况作一次调查，市政府调查小组随机抽查了其中100户家庭一年的月平均用水量（单位：吨）.并将调查结果制成了如图所示的条形统计图.

(1)、请将条形统计图补充完整；

(2)、求这100个样本数据的平均数，众数和中位数。

(3)、根据样本数据，估计该小区500户家庭中月平均用水量超过12吨的约有多少户？

查看试题解析
25. 如图所示，一个农户要建一个矩形猪舍，猪舍的一边利用长为12m的房墙，另外三边用25m长的建筑材料围成，为了方便进出，在垂直于房墙的一边留一个1m宽的门.所围成矩形猪舍的长、宽分别是多少时，猪舍面积为80m²？

查看试题解析
26. 某批发商以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件，第二个月如果单价不变，预计仍可以售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降10元，可多售出100件，但最低单价应高于购进的价格；第二月结束后.批发商核对剩余的T恤一次性清仓销售，清仓时单价为40元，设第二个月单价降低x元.

(1)、填表（不需化简）

时间

第一个月

第二个月

清仓时

单价（元）

80

40

销售量

200

(2)、如果批发商希望通过销售这批T恤获利8750元，那么第二个月的单价应该是多少？

(3)、如果批发商希望通过销售这批T恤获利最大，那么最大利润可达到多少元？(直接写出答案)

查看试题解析
27. 如图，四边形ACDE是证明勾股定理时用到的一个图形，a、b、c是Rt△ABC和Rt△BED边长，易知AE= $\sqrt{2}$ c，这时我们把关于x的形如ax²+ $\sqrt{2} c x$ +b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题：

(1)、写出一个“勾系一元二次方程”；

(2)、求证：关于x的“勾系一元二次方程”ax²+ $\sqrt{2} c x$ +b=0必有实数根；

(3)、若x=-1是“勾系一元二次方程”ax²+ $\sqrt{2} c x$ +b=0的一个根，且四边形ACDE的周长是
12 $\sqrt{2}$ ，求△ABC面积.

查看试题解析

时间	第一个月	第二个月	清仓时
单价（元）	80		40
销售量	200

x	0.59	0.60	0.61	0.62	0.63
x²+x-1	-0.061	-0.04	-0.017	0.0044	0.0269