浙江省宁波市鄞州区七校2021届九年级下学期数学第一次月考联考试卷
试卷更新日期:2021-04-13 类型:月考试卷
一、选择题(每小题4分,共40分.)
-
1. 若9x=5y,则 =( )A、 B、 C、 D、2. 下列事件是随机事件的是( )A、抛一枚质地均匀的硬币,正好正面朝上 B、掷一枚质地均匀的骰子,出现点数为7 C、从一副扑克牌中任抽2张都是红心5 D、从装满红球的口袋中随意摸一个球是红球3. 下列二次函数的图象的对称轴是y轴的是( )A、y=-(x+1)2+1 B、y=(x-1)2+1 C、y=-(x-1)2+1 D、y=-x2+14. 如图,该几何体是由4个相同的小正方体搭建而成的,则它的左视图是( )
 A、
A、 B、
B、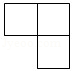 C、
C、 D、
D、 5. 已知点A(1,y1),B(-2,y2),C(0,y3)是抛物线y=-x2+2x+1上的三个点,则( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y2<y1 D、y2<y3<y16. 如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
5. 已知点A(1,y1),B(-2,y2),C(0,y3)是抛物线y=-x2+2x+1上的三个点,则( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y2<y1 D、y2<y3<y16. 如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )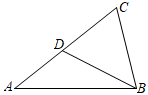 A、2 B、 C、 D、47. 如图,AC为⊙O的弦,B为优弧ABC上任意一点,过点O作AB的平行线交⊙O于点D,交弦AC于点E,连结OA,其中∠OAB=20°,∠CDO=40°,则∠CED=( )
A、2 B、 C、 D、47. 如图,AC为⊙O的弦,B为优弧ABC上任意一点,过点O作AB的平行线交⊙O于点D,交弦AC于点E,连结OA,其中∠OAB=20°,∠CDO=40°,则∠CED=( ) A、50° B、60° C、70° D、80°8. 如图,在△ABC中,E是线段AC上一点,且AE∶CE=1∶2,过点C作CD∥AB,交BE的延长线于点D.若△BCE的面积等于4,则△CDE的面积等于( )
A、50° B、60° C、70° D、80°8. 如图,在△ABC中,E是线段AC上一点,且AE∶CE=1∶2,过点C作CD∥AB,交BE的延长线于点D.若△BCE的面积等于4,则△CDE的面积等于( ) A、8 B、16 C、24 D、329. 如图,小明家附近有一观光塔CD,他发现当光线角度发生变化时,观光塔的影子在地面上的长度也发生变化.经测量发现,当小明站在点A处时,塔顶D的仰角为37°,他继续往前再走5米到达点B(点A,B,C在同一直线上),此时塔顶D的仰角为53°,则观光塔CD的高度约为( )(精确到0.1米,参考数值: , )
A、8 B、16 C、24 D、329. 如图,小明家附近有一观光塔CD,他发现当光线角度发生变化时,观光塔的影子在地面上的长度也发生变化.经测量发现,当小明站在点A处时,塔顶D的仰角为37°,他继续往前再走5米到达点B(点A,B,C在同一直线上),此时塔顶D的仰角为53°,则观光塔CD的高度约为( )(精确到0.1米,参考数值: , )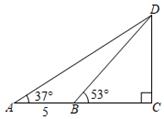 A、7.6米 B、7.8米 C、8.6米 D、8.8米10. 如图,点A是二次函数 图象上的一点,且位于第一象限,点B是直线 上一点,点B′与点B关于原点对称,连结AB,AB′,若△ABB′为等边三角形,则点A的坐标是( )
A、7.6米 B、7.8米 C、8.6米 D、8.8米10. 如图,点A是二次函数 图象上的一点,且位于第一象限,点B是直线 上一点,点B′与点B关于原点对称,连结AB,AB′,若△ABB′为等边三角形,则点A的坐标是( )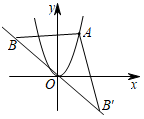 A、( , ) B、( , ) C、(1, ) D、( , )
A、( , ) B、( , ) C、(1, ) D、( , )二、填空题(每小题5分,共30分)
-
11. 在Rt△ABC中,∠C=90°,AC=3,BC=4,则tanA=.12. 某市对一批口罩进行抽检,统计合格口罩的只数,得到口罩的合格频率如下:
抽检只数(只)
50
100
150
500
1 000
2 000
10 000
50 000
合格频率
0.82
0.83
0.82
0.83
0.84
0.84
0.84
0.84
则从该批口罩中任抽一只口罩,是合格品的概率约为.
13. 如图,点A,B,C都在⊙O上,若OB=3,∠ABC=30°,则劣弧AC的长为.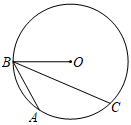 14. 将二次函数y=x2+2的图象先向左平移2个单位长度,再向下平移3个单位长度,所得新抛物线的函数表达式为.15. 如图,⊙O的半径为4,AB为⊙O的直径,∠ABC=90°,直线CE与⊙O相切于点D,交BA的延长线于点E,A为OE的中点,则AC的长是.
14. 将二次函数y=x2+2的图象先向左平移2个单位长度,再向下平移3个单位长度,所得新抛物线的函数表达式为.15. 如图,⊙O的半径为4,AB为⊙O的直径,∠ABC=90°,直线CE与⊙O相切于点D,交BA的延长线于点E,A为OE的中点,则AC的长是.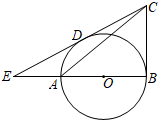 16. 如图,在△ABC中,AB=2, ,D为△ABC内部的一点,且CD⊥BD,在BD的延长线上取一点E,使得∠CAE=∠BAD.若∠ADE=∠ABC,且∠DBC=30°,则AD的长为.
16. 如图,在△ABC中,AB=2, ,D为△ABC内部的一点,且CD⊥BD,在BD的延长线上取一点E,使得∠CAE=∠BAD.若∠ADE=∠ABC,且∠DBC=30°,则AD的长为.
三、解答题(本大题有8小题,共80分)
-
17.(1)、计算: ;(2)、若 ,求 的值.18. 小刚所在的社区为了做好应对新冠疫情的防控工作,特招募社区抗疫志愿工作者.小刚的爸爸决定报名参加,根据规定,志愿者会被随机分到A(体温检测),B(便民代购),C(环境消杀)其中一组.(1)、求小刚的爸爸被分到C组的概率;(2)、小明的爸爸也加入了该社区的志愿者队伍,请利用画树状图或列表的方法求小明的爸爸和小刚的爸爸被分到同一组的概率.19. 近几年中学生近视的现象越来越严重,为响应国家的号召,某公司推出了如图1所示的护眼灯,其侧面示意图(台灯底座高度忽略不计)如图2所示,其中灯柱BC=18 cm,灯臂CD=33 cm,灯罩DE=20 cm,BC⊥AB,CD,DE分别可以绕点C,D上下调节一定的角度.经使用发现:当∠DCB=140°,且ED∥AB时,台灯光线最佳.求此时点D到桌面AB的距离.(精确到0.1 cm,参考数值:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
 20. 如图,在7×7的正方形网格中,每个小正方形的边长均为1,线段AB的端点均在小正方形的格点上(小正方形的顶点称为格点).
20. 如图,在7×7的正方形网格中,每个小正方形的边长均为1,线段AB的端点均在小正方形的格点上(小正方形的顶点称为格点). (1)、在图中画一个Rt△ABC,使其同时满足以下三个条件:
(1)、在图中画一个Rt△ABC,使其同时满足以下三个条件:①A为直角顶点;②点C在格点上;③ ;
(2)、在(1)的条件下,请在网格中找到另一个格点D,满足tan∠CBD=1,连结CD,求线段CD的长.
21. 如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连结DE. (1)、若∠ABC=20°,求∠DEA的度数;(2)、若AC=3,AB=4,求CD的长.22. 如图,已知二次函数y=-x2+bx+c的图象经过A(2,0),B(0,-8)两点.
(1)、若∠ABC=20°,求∠DEA的度数;(2)、若AC=3,AB=4,求CD的长.22. 如图,已知二次函数y=-x2+bx+c的图象经过A(2,0),B(0,-8)两点. (1)、求该二次函数的表达式;(2)、当2≤x≤5时,函数在点C处取得最大值,在点D处取得最小值,求△BCD的面积.23. 如图,在平面直角坐标系中,点A的坐标为(4,0),B是y轴正半轴上的一个动点,以OA为直径作圆,交AB于点C.
(1)、求该二次函数的表达式;(2)、当2≤x≤5时,函数在点C处取得最大值,在点D处取得最小值,求△BCD的面积.23. 如图,在平面直角坐标系中,点A的坐标为(4,0),B是y轴正半轴上的一个动点,以OA为直径作圆,交AB于点C.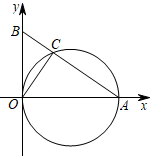 (1)、求证:△AOB∽△ACO;(2)、当∠OAB=30°时,求点C到x轴的距离;(3)、求 的最大值.24. 定义:有一组邻边垂直且对角线相等的四边形称为垂等四边形.
(1)、求证:△AOB∽△ACO;(2)、当∠OAB=30°时,求点C到x轴的距离;(3)、求 的最大值.24. 定义:有一组邻边垂直且对角线相等的四边形称为垂等四边形. (1)、写出一个已学的特殊平行四边形中是垂等四边形的是;(2)、如图1,在正方形ABCD中,点E,F,G分别在AD,AB,BC上,四边形DEFG是垂等四边形,且∠EFG=90°,AF=CG.
(1)、写出一个已学的特殊平行四边形中是垂等四边形的是;(2)、如图1,在正方形ABCD中,点E,F,G分别在AD,AB,BC上,四边形DEFG是垂等四边形,且∠EFG=90°,AF=CG.①求证:EG=DG;
②若BC=n·BG,求n的值;
(3)、如图2,在Rt△ABC中, , ,以AB为对角线,作垂等四边形ACBD.过点D作CB的延长线的垂线,垂足为E,且△ACB与△DBE相似,求四边形ACBD的面积.