浙江省温州市苍南县2021年数学中考一模试卷
试卷更新日期:2021-04-13 类型:中考模拟
一、单选题
-
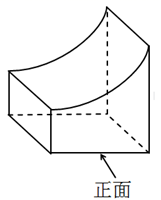
1. 在-4,-2,0,1,3,5这六个数中,任意三数之积的最大值是( )A、15 B、40 C、24 D、302. 如图所示的几何体的从左面看到的图形为( )
 A、
A、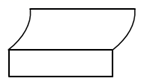 B、
B、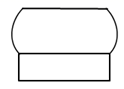 C、
C、 D、
D、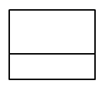 3. 某校为了解学生的课外阅读情况,随机抽取了一个班的学生,对他们一周的课外阅读时间进行了统计,统计数据如下表,则该班学生一周课外阅读时间的中位数和众数分别是 ( )
3. 某校为了解学生的课外阅读情况,随机抽取了一个班的学生,对他们一周的课外阅读时间进行了统计,统计数据如下表,则该班学生一周课外阅读时间的中位数和众数分别是 ( )读书时间
6 小时及以下
7 小时
8 小时
9 小时
10 小时及以上
学生人数
6
11
8
8
7
A、8,7 B、8,8 C、8.5,8 D、8.5,74. 已知M、N两点关于y轴对称,且点M在反比例函数 的图象上,点N在直线y=x+4上,设点M的坐标为(a,b),则二次函数y=﹣abx2+(a+b)x有( )A、最小值为2 B、最大值为2 C、最小值为﹣2 D、最大值为﹣25. 在一只不透明的口袋中放入只有颜色不同的白球6个,黑球8个,黄球n个,搅匀后随机从中摸取一个恰好是黄球的概率为 ,则放入的黄球个数n=( )A、4 B、5 C、6 D、76. 不等式组 的解集为( )A、x≥-2 B、-2<x<3 C、x>3 D、-2≤3<37. 已知点(m,﹣2)关于原点对称的点落在直线y=x﹣3上,则m的值为( )A、﹣5 B、﹣2 C、1 D、28. 一副学生三角板放在一个圈里恰好如图所示,顶点 在圆圈外,其他几个顶点都在圆圈上,圆圈和 交于点 ,已知 ,则这个圆圈上的弦 长是( ) A、 B、 C、 D、9. 若x、y满足方程组 ,则x﹣y的值为( )A、﹣2 B、﹣1 C、1 D、210. 如图,在△ABC中,∠ACB=90°,CD、CE分别是高和角平分线,已知△BEC的面积是15,△CDE的面积为3,则△ABC的面积为( )
A、 B、 C、 D、9. 若x、y满足方程组 ,则x﹣y的值为( )A、﹣2 B、﹣1 C、1 D、210. 如图,在△ABC中,∠ACB=90°,CD、CE分别是高和角平分线,已知△BEC的面积是15,△CDE的面积为3,则△ABC的面积为( ) A、22.5或20 B、22.5 C、24或20 D、20
A、22.5或20 B、22.5 C、24或20 D、20二、填空题
-
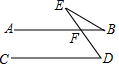
11. 因式分解: .12. 如图,AB//CD,∠D=60°,FB=FE,则∠E=°.
 13. 若关于x的一元二次方程x2﹣4x+m﹣1=0有两个相等的实数根,则m的值为.14. 一个箱子内有3颗相同的球,将3颗球分别标示号码1,2,5,今浩浩以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球10次,现已取了8次,取出的结果依次为1,2,2,5,5,2,1,2,若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分数,浩浩打算依计划继续从箱子取球2次,则发生“这10次得分的平均数在2.2~2.4之间(含2.2,2.4)”的情形的概率为.15. 将双曲线y= 向右平移1个单位长度,再向下平移2个单位长度,得到的新双曲线与直线y=kx﹣2﹣k(k>0)相交于两点,其中一个点的横坐标为a,另一个点的纵坐标为b,则(a﹣1)(b+2)=.16. 如图,AB为⊙O的直径,弦CD⊥AB于点E,点F在圆上,且 ,BE=2,CD=8,CF交AB于点G,则弦CF的长为 , AG的长为.
13. 若关于x的一元二次方程x2﹣4x+m﹣1=0有两个相等的实数根,则m的值为.14. 一个箱子内有3颗相同的球,将3颗球分别标示号码1,2,5,今浩浩以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球10次,现已取了8次,取出的结果依次为1,2,2,5,5,2,1,2,若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分数,浩浩打算依计划继续从箱子取球2次,则发生“这10次得分的平均数在2.2~2.4之间(含2.2,2.4)”的情形的概率为.15. 将双曲线y= 向右平移1个单位长度,再向下平移2个单位长度,得到的新双曲线与直线y=kx﹣2﹣k(k>0)相交于两点,其中一个点的横坐标为a,另一个点的纵坐标为b,则(a﹣1)(b+2)=.16. 如图,AB为⊙O的直径,弦CD⊥AB于点E,点F在圆上,且 ,BE=2,CD=8,CF交AB于点G,则弦CF的长为 , AG的长为.
三、解答题
-
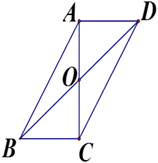
17.(1)、计算: ﹣(﹣1)2020﹣(π﹣2)0;(2)、分解因式:3x3﹣12x;(3)、计算:(﹣a﹣1)2﹣(1+a)(a﹣1);(4)、解方程: .18. 如图,在四边形ABCD中,对角线AC、BD相交于点O,若BC=4,AO=CO=3,BD=10,∠ACB=90°,求AD的长及四边形ABCD的面积.
 19. 如图
19. 如图
 (1)、已知线段a、以此为边,用尺规作图(保留作图痕迹,不需写作法)作出一个含有60°的菱形;(2)、如图,在菱形ABCD中,点M、N分别是边BC、CD上的点,连接AM、AN,若∠ABC=∠MAN=60°,求证:BM=CN;20. 已知抛物线 经过点 和点 .(1)、求抛物线的解析式;(2)、将(1)中的抛物线平移,使其顶点坐标为 ,平移后的抛物线与 轴的两个交点分别为点 (点 在点 的左边).求点 的坐标;(3)、将(1)中的抛物线平移,设其顶点的纵坐标为 ,平移后的抛物线与 轴两个交点之间的距离为 .若 ,直接写出 的取值范围.21. 某校学生的数学期末总评成绩由参与教学活动、作业、期末考试成绩3部分组成.各部分所占比例如图所示.小明参与数学活动、作业和期末考试得分依次为84分、92分、88分.则小明的数学期末总评成绩是多少?
(1)、已知线段a、以此为边,用尺规作图(保留作图痕迹,不需写作法)作出一个含有60°的菱形;(2)、如图,在菱形ABCD中,点M、N分别是边BC、CD上的点,连接AM、AN,若∠ABC=∠MAN=60°,求证:BM=CN;20. 已知抛物线 经过点 和点 .(1)、求抛物线的解析式;(2)、将(1)中的抛物线平移,使其顶点坐标为 ,平移后的抛物线与 轴的两个交点分别为点 (点 在点 的左边).求点 的坐标;(3)、将(1)中的抛物线平移,设其顶点的纵坐标为 ,平移后的抛物线与 轴两个交点之间的距离为 .若 ,直接写出 的取值范围.21. 某校学生的数学期末总评成绩由参与教学活动、作业、期末考试成绩3部分组成.各部分所占比例如图所示.小明参与数学活动、作业和期末考试得分依次为84分、92分、88分.则小明的数学期末总评成绩是多少? 22. 在平面直角坐标系中,矩形OABC的边OC、OA分别在x轴、y轴上,点A(0,m),点C(n,0),且m、n满足 + =0.
22. 在平面直角坐标系中,矩形OABC的边OC、OA分别在x轴、y轴上,点A(0,m),点C(n,0),且m、n满足 + =0. (1)、求点A、C的坐标;(2)、如图1,点D为第一象限内一动点,连CD、BD、OD,∠ODB=90°,试探究线段CD、OD、BD之间的数量关系,并证明你的结论;(3)、如图2,点F在线段OA上,连BF,作OM⊥BF于M,AN⊥BF于N,当F在线段OA上运动时(不与O、A重合), 的值是否变化?若变化,求出变化的范围;若不变,求出其值.23. 如图1是某体育看台侧面的示意图,观众区AC的坡度i=1:2,顶端C离水平地面AB的高度为15m,顶棚外沿处的点E恰好在点A的正上方,从D处看E处的仰角α=30°,竖直的立杆上C,D两点间的距离为5m.
(1)、求点A、C的坐标;(2)、如图1,点D为第一象限内一动点,连CD、BD、OD,∠ODB=90°,试探究线段CD、OD、BD之间的数量关系,并证明你的结论;(3)、如图2,点F在线段OA上,连BF,作OM⊥BF于M,AN⊥BF于N,当F在线段OA上运动时(不与O、A重合), 的值是否变化?若变化,求出变化的范围;若不变,求出其值.23. 如图1是某体育看台侧面的示意图,观众区AC的坡度i=1:2,顶端C离水平地面AB的高度为15m,顶棚外沿处的点E恰好在点A的正上方,从D处看E处的仰角α=30°,竖直的立杆上C,D两点间的距离为5m. (1)、求观众区的水平宽度AB.(2)、求图1中点E离水平地面的高度EA.(3)、因为遮阳需要,现将顶棚ED绕D点逆时针转动11°30′,若E点在地面上的铅直投影是点F(图2),求AF.(sin11°30′≈0.20,cos11°30′≈0.98,tan11°30′≈0.20;sin18°30′≈0.32,cos18°30′≈0.95,tan18°30′≈0.33,结果精确到0.1m)24. 如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过C作CD//AB,CD交⊙O于D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)、求观众区的水平宽度AB.(2)、求图1中点E离水平地面的高度EA.(3)、因为遮阳需要,现将顶棚ED绕D点逆时针转动11°30′,若E点在地面上的铅直投影是点F(图2),求AF.(sin11°30′≈0.20,cos11°30′≈0.98,tan11°30′≈0.20;sin18°30′≈0.32,cos18°30′≈0.95,tan18°30′≈0.33,结果精确到0.1m)24. 如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过C作CD//AB,CD交⊙O于D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF. (1)、求证:AF是⊙O的切线;(2)、求证:AB2﹣BE2=BE•EC;(3)、如图2,若点G是△ACD的内心,BC•BE=64,求BG的长.
(1)、求证:AF是⊙O的切线;(2)、求证:AB2﹣BE2=BE•EC;(3)、如图2,若点G是△ACD的内心,BC•BE=64,求BG的长.