贵州省毕节市2021年数学中考二模试卷
试卷更新日期:2021-04-13 类型:中考模拟
一、单选题
-
1. 下列各式中正确的是( )A、 B、 C、 D、
-
2. 2020年中央财政下达义务教育补助经费1695.9亿元,比上年增长8.3%.其中1695.9亿元用科学记数法表示为( )A、 元 B、 元 C、 元 D、 元
-
3. 如图,将小立方块①从6个大小相同的小立方块所搭的几何体中移走后,所得几何体( )
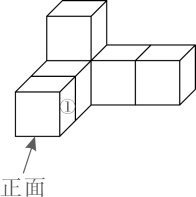 A、主视图改变,左视图改变 B、俯视图不变,左视图改变 C、俯视图改变,左视图改变 D、主视图不变,左视图不变
A、主视图改变,左视图改变 B、俯视图不变,左视图改变 C、俯视图改变,左视图改变 D、主视图不变,左视图不变 -
4. 如图.随机闭合开关K1、K2、K3中的两个,则能让两盏灯泡L1、L2同时发光的概率为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5. 下列图案既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
6. 在课外活动中,有10名同学进行了投篮比赛,限每人投10次,投中次数与人数如下表:
投中次数
5
7
8
9
10
人数
2
3
3
1
1
则这10人投中次数的平均数和中位数分别是( )
A、 B、 C、 D、 -
7. 下列计算结果正确的是( )A、 B、 C、 D、
-
8. 《九章算术》中记载“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?此问题中羊价为( )A、160钱 B、155钱 C、150钱 D、145钱
-
9. 已知正比例函数 的图象过点 ,把正比例函数 的图象平移,使它过点 ,则平移后的函数图象大致是( )A、
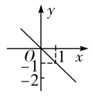 B、
B、 C、
C、 D、
D、
-
10. 点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )A、 B、4 C、﹣ D、﹣
-
11. 下列命题正确的是( )A、若分式 的值为0,则x的值为±2. B、一个正数的算术平方根一定比这个数小. C、若 ,则 . D、若 ,则一元二次方程 有实数根.
-
12. 在螳螂的示意图中,AB∥DE,△ABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD=( )

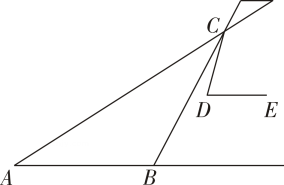 A、16° B、28° C、44° D、45°
A、16° B、28° C、44° D、45° -
13. 如图,在 中, ,D是 的中点, ,交 的延长线于点E . 若 , ,则 的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14. 如图,在平面直角坐标系中,直线 与x轴、y轴分别交于点A和点 是线段 上一点,过点C作 轴,垂足为D , 轴,垂足为E , .若双曲线 经过点C , 则k的值为( )
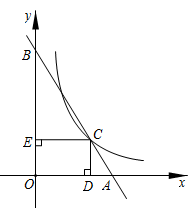 A、 B、 C、 D、
A、 B、 C、 D、 -
15. 如图,在 中, , ,按以下步骤作图:(1)分别以点 为圆心,以大于 的长为半径作弧,两弧相交于 两点(点M在 的上方);(2)作直线 交 于点O , 交 于点D;(3)用圆规在射线 上截取 .连接 ,过点O作 ,垂足为F , 交 于点G . 下列结论:
① ;② ;③ ;④若 ,则四边形 的周长为25.
其中正确的结论有( )
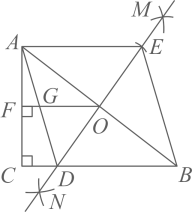 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个
二、填空题
-
16. 若 ,则 .
-
17. 关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是 .
-
18. 分式方程 的解是 .
-
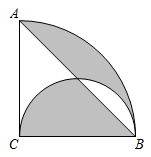
19. 如图,圆心角为 的扇形 内,以 为直径作半圆,连接 .若阴影部分的面积为 ,则 .
-
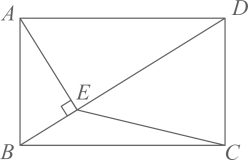
20. 如图,在矩形 中, 是对角线, ,垂足为E , 连接 .若 ,则如 的值为 .
三、解答题
-
21. 计算:
-
22. 先化简 ,然后从-3,0,1,3中选一个合适的数代入求值.
-
23. 为了发展学生的健康情感,学校开展多项体育活动比赛,促进学生加强体育锻炼,注重增强体质,从全校2100名学生60秒跳绳比赛成绩中,随机抽取60名同学的成绩,通过分组整理数据得到下面的样本频数分布表.
跳绳的次数
频数
4
6
11
22
10
4
(1)、已知样本中最小的数是60,最大的数是198,组距是20,请你将该表左侧的每组数据补充完整;(2)、估计全校学生60秒跳绳成绩能达到最好一组成绩的人数;(3)、若以各组组中值代表各组的实际数据,求出样本平均数(结果保留整数)及众数;分别写出用样本平均数和众数估计全校学生60秒跳绳成绩得到的推断性结论. -
24. 天水市某商店准备购进A、B两种商品,A种商品每件的进价比B种商品每件的进价多20元,用2000元购进A种商品和用1200元购进B种商品的数量相同.商店将A种商品每件的售价定为80元,B种商品每件的售价定为45元.(1)、A种商品每件的进价和B种商品每件的进价各是多少元?(2)、商店计划用不超过1560元的资金购进A、B两种商品共40件,其中A种商品的数量不低于B种商品数量的一半,该商店有几种进货方案?(3)、“五一”期间,商店开展优惠促销活动,决定对每件A种商品售价优惠 元,B种商品售价不变,在(2)的条件下,请设计出m的不同取值范围内,销售这40件商品获得总利润最大的进货方案.
-
25. 如图,在△ABC中,D是边BC上一点,以BD为直径的⊙O经过点A,且∠CAD=∠ABC.
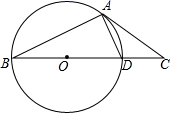 (1)、请判断直线AC是否是⊙O的切线,并说明理由;(2)、若CD=2,CA=4,求弦AB的长.
(1)、请判断直线AC是否是⊙O的切线,并说明理由;(2)、若CD=2,CA=4,求弦AB的长. -
26. (了解概念)有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.

(理解运用)
(1)、如图①,对余四边形ABCD中,AB=5,BC=6,CD=4,连接AC.若AC=AB,求sin ∠CAD的值;(2)、如图②,凸四边形ABCD中,AD=BD,AD⊥BD,当2CD2+CB2=CA2时,判断四边形ABCD是否为对余四边形.证明你的结论. -
27. 已知二次函数y=x2+bx+c(a≠0)的图象与x轴交于A,B(1,0)两点,与y轴交于点C(0,-3).(1)、求二次函数的表达式及点A的坐标;(2)、点D是二次函数图象上位于第三象限内的点,求点D到直线AC的距离取得最大值时点D的坐标;(3)、点M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N.使以M,N,B,O为顶点的四边形是平行四边形?若有,请写出点N的坐标(不写求解过程).
