重庆第八中2020-2021学年八年级下学期数学开学试卷
试卷更新日期:2021-04-13 类型:开学考试
一、单选题
-
1. 函数 的自变量x的取值范围是( )A、 B、 且 C、 D、2. 下列因式分解正确的是( )A、 B、 C、 D、3. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、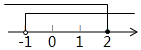 C、
C、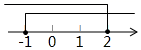 D、
D、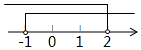 4. 如图,将△ABC绕点C按逆时针方向旋转至△DEC,使点D落在BC的延长线上.已知∠A=33°,∠B=30°,则∠ACE的大小是( )
4. 如图,将△ABC绕点C按逆时针方向旋转至△DEC,使点D落在BC的延长线上.已知∠A=33°,∠B=30°,则∠ACE的大小是( ) A、63° B、58° C、54° D、52°5. 将点 ,先向右平移4个单位,再向下平移4个单位,则平移后得到点为( )A、 B、 C、 D、6. 在抗击“新型冠状病毒肺炎”疫情中,某社区志愿者小分队年龄如表:
A、63° B、58° C、54° D、52°5. 将点 ,先向右平移4个单位,再向下平移4个单位,则平移后得到点为( )A、 B、 C、 D、6. 在抗击“新型冠状病毒肺炎”疫情中,某社区志愿者小分队年龄如表:年龄(岁)
18
22
30
35
43
人数
2
3
2
2
1
则这10名队员年龄的中位数、众数分别是( )
A、20岁,35岁 B、22岁,22岁 C、26岁、22岁 D、30岁,30岁7. 若点 , 都在一次函数 的图象上,则 与 的大小关系是( )A、 B、 C、 D、不能确定8. 为了打造“绿洲”,计划在市内一块如图所示的三角形空地上种植某种草皮,已知 米, 米, ,这种草皮每平方米售价 元,则购买这种草皮需要( )元.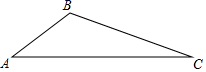 A、 B、 C、 D、9. 天虹商场现销售某品牌运动套装,上衣和裤子一套售价500元.若将上衣价格下调5%,将裤子价格上调8%,则这样一套运动套装的售价提高0.2%.设上衣和裤子在调价前单价分别为x元和y元,则可列方程组为( )A、 B、 C、 D、10. 如图,O是正 内一点, , , .将线段 以点B为旋转中心逆时针旋转60°得到线段 ,下列结论错误的是( )
A、 B、 C、 D、9. 天虹商场现销售某品牌运动套装,上衣和裤子一套售价500元.若将上衣价格下调5%,将裤子价格上调8%,则这样一套运动套装的售价提高0.2%.设上衣和裤子在调价前单价分别为x元和y元,则可列方程组为( )A、 B、 C、 D、10. 如图,O是正 内一点, , , .将线段 以点B为旋转中心逆时针旋转60°得到线段 ,下列结论错误的是( )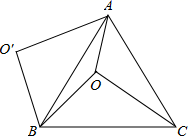 A、点O与 的距离为4 B、 C、S四边形AOBO′ D、11. 已知 , , ,则 的值为( )A、9 B、6 C、4 D、无法确定12. 如果关于x的不等式组 的解集为 ,且整数m使得关于x,y的二元一次方程组 的解为整数(x,y均为整数),则不符合条件的整数m的有( )A、-4 B、2 C、4 D、5
A、点O与 的距离为4 B、 C、S四边形AOBO′ D、11. 已知 , , ,则 的值为( )A、9 B、6 C、4 D、无法确定12. 如果关于x的不等式组 的解集为 ,且整数m使得关于x,y的二元一次方程组 的解为整数(x,y均为整数),则不符合条件的整数m的有( )A、-4 B、2 C、4 D、5二、填空题
-
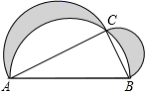
13. 若点 和 关于原点对称,则 的值是.14. 如图: , 的面积为20,在 的同侧,分别以 , , 为直径作三个半圆,则阴影部分(即“希波克拉底月牙形”)的面积为.
 15. 已知二元一次方程组 的解为 ,则在同一平面直角坐标系中,直线l1:y=x+5与直线l2:y=- x-1的交点坐标为.16. 小明去买文具,打算购买5支单价相同的签字笔和3本单价相同的笔记本,期间他与售货员对话如下:
15. 已知二元一次方程组 的解为 ,则在同一平面直角坐标系中,直线l1:y=x+5与直线l2:y=- x-1的交点坐标为.16. 小明去买文具,打算购买5支单价相同的签字笔和3本单价相同的笔记本,期间他与售货员对话如下:小明:您好,我要买5支签字笔和3本笔记本.
售货员:好的,那你应该付52元.
小明:刚才我把两种文具的单价弄反了,以为要付44元.
那么购买1支签字笔和1本笔记本应付元.
17. 如图,把一个含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到 ,已知 ,则在旋转过程中点A经过的路径长为.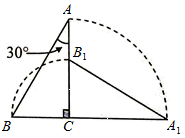 18. 星期六下午,小张和小王同时从学校沿相同的路线去书店买书,小王出发4分钟后发现忘记带钱包,立即调头按原速原路回学校拿钱包,小王拿到钱包后,以比原速提高20%的速度按原路赶去书店,结果还是比小张晚4分钟到书店(小王拿钱包的时间忽略不计).在整个过程中,小张保持匀速运动,小王提速前后也分别保持匀速运动,如图所示是小张与小王之间的距离y(米)与小王出发的时间x(分钟)之间的函数图象,则学校到书店的距离为米.
18. 星期六下午,小张和小王同时从学校沿相同的路线去书店买书,小王出发4分钟后发现忘记带钱包,立即调头按原速原路回学校拿钱包,小王拿到钱包后,以比原速提高20%的速度按原路赶去书店,结果还是比小张晚4分钟到书店(小王拿钱包的时间忽略不计).在整个过程中,小张保持匀速运动,小王提速前后也分别保持匀速运动,如图所示是小张与小王之间的距离y(米)与小王出发的时间x(分钟)之间的函数图象,则学校到书店的距离为米.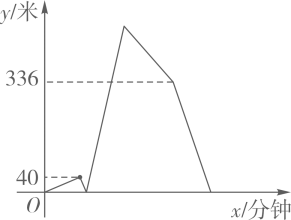 19. 在平面直角坐标系中,已知y轴上一点 ,A为x轴上的一动点,连接 ,以 为边作等边 如图所示,连接 ,则 的最小值是.
19. 在平面直角坐标系中,已知y轴上一点 ,A为x轴上的一动点,连接 ,以 为边作等边 如图所示,连接 ,则 的最小值是.
三、解答题
-
20. 因式分解:(1)、(2)、21. 解方程组或不等式组,并把解集画数轴上:(1)、(2)、22. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, 的顶点均在格点上.

( 1 )画出 关于原点对称的 ,并写出 , , 的坐标;
( 2 )画出 向上平移4个单位后的 ,并求平移过程中 扫过的面积.
23. 某校为了解七、八年级学生对旧历新年传统风俗知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析,部分信息如下:a.七年级成绩频数分布直方图
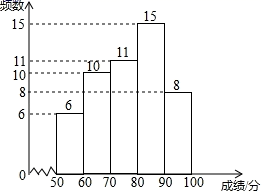
b.七年级成绩在 这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级
平均数
中位数
七
76.9
m
八
79.2
79.5
根据以上信息,回答下列问题:
(1)、在这次测试中,七年级在80分以上(含80分)的有人;(2)、表中m的值为(3)、在这次测试中,七年级学生甲与八年级学生乙的成绩都是79分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;(4)、该校七年级学生有1600人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.24. 春节期间,根据习俗每家每户都会在门口挂红灯笼和贴对联,某商店看准了商机,准备购进一批红灯笼和对联进行销售,已知每副对联的进价比每个红灯笼的进价少10元:且购进对联50副比购进红灯笼20个多花费40元.(1)、对联和红灯笼的单价分别为多少?(2)、由于销售火爆,第一批售完后,该商店以相同的进价再购进300副对联和200个红灯笼,已知对联的销售价格为12元一副,红灯笼的销售价格为24元一个,销售一段时间后发现对联售出了总数的 ,红灯笼售出了总数的 ,为了清仓,该店老板决定对剩下的红灯笼和对联以相同的折扣数打折销售,并很快全部售出,问商店最低打几折,才能使总的利润率不低于20%?25. 阅读下列材料,回答问题:材料一:在大于1的整数中,除了能被1和本身整除外,还能被其它数(0除外)整除的数,称为合数.
材料二:若一个各个数位上的数字都不为零的四位数,其千位上的数字与个位上的数字相等,百位上的数字与十位上的数字相等,且该数前两位数字组成的两位数和后两位数字组成的两位数都是合数,则称该数为“对称合数”,如2552,6886都是“对称合数”.
(1)、最小的“对称合数”为 , 最大的“对称合数”为;(2)、若“对称合数”的前两位数字组成的两位数和后两位数字组成的两位数之和是完全平方数,求满足条件的所有“对称合数”的个数,并把它们写出来.26. 如图, 中, , ,点D在 边上. (1)、如图1,若 且 ,求 的长;(2)、如图2,过B作 ,且 .连接 并延长交 于点F,过点C作 于点G,连接 .求证: .27. 如图,在平面直角坐标系中,直线 : ( )分别与x轴、y轴交于A、B两点,其中 ,点C在x轴的正半轴上,且 .
(1)、如图1,若 且 ,求 的长;(2)、如图2,过B作 ,且 .连接 并延长交 于点F,过点C作 于点G,连接 .求证: .27. 如图,在平面直角坐标系中,直线 : ( )分别与x轴、y轴交于A、B两点,其中 ,点C在x轴的正半轴上,且 .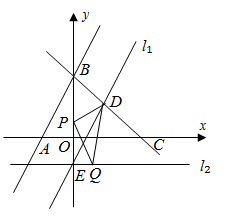
 (1)、求 的面积:(2)、将直线 向下平移6个单位长度得到直线 ,直线 与y轴交于点E,与直线 交于点D,过点E作y轴的垂线 ,若点P为y轴上一个动点,Q为直线 上一个动点,求 的周长的最小值:(3)、在(2)的条件下,直线 上找一点M,使得 是等腰三角形,若存在,求出点M的坐标;若不存在,说明理由.
(1)、求 的面积:(2)、将直线 向下平移6个单位长度得到直线 ,直线 与y轴交于点E,与直线 交于点D,过点E作y轴的垂线 ,若点P为y轴上一个动点,Q为直线 上一个动点,求 的周长的最小值:(3)、在(2)的条件下,直线 上找一点M,使得 是等腰三角形,若存在,求出点M的坐标;若不存在,说明理由.