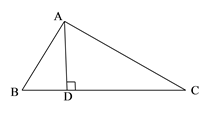初中数学北师大版七年级下学期 第四章 单元测试卷
试卷更新日期：2021-04-13 类型：单元试卷
一、单选题
-
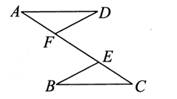
1. 在下列长度的四根木棒中，能与2m、5m长的两根木棒钉成一个三角形的是（ ）A、2m B、3m C、5m D、7m2. 等腰三角形两边长为3和6，则周长为（ ）A、12 B、15 C、12或15 D、无法确定3. 如图，若△ABC≌△DEF，BE＝22，BF＝5，则FC的长度是（ ）
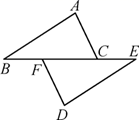A、10 B、12 C、8 D、164. 如图所示是两个全等三角形，由图中条件可知，
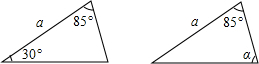A、 B、 C、 D、 或5. 如图，△ABC≌△CDA，∠BAC＝∠DCA，则BC 的对应边是 （ ）
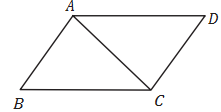A、CD B、CA C、DA D、AB6. 如图，在 中， 于 ， 于 ， 与 交于点 ．请你添加一个适当的条件，使 ≌ ．下列添加的条件错误的是（ ）
A、 B、 C、 D、7. 如图，已知AC平分∠DAB，CE⊥AB于E，AB=AD+2BE，则下列结论：①AB+AD=2AE；②∠DAB+∠DCB=180°；③CD=CB；④S△ACE﹣2S△BCE=S△ADC；其中符合题意结论的个数是（ ）
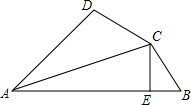A、1个 B、2个 C、3个 D、4个8. 如图，点P在∠MAN的角平分线上，点B，C分别在AM，AN上，作PR⊥AM，PS⊥AN，垂足分别是R，S．若∠ABP+∠ACP=180°，则下面三个结论：①AS=AR；②PC∥AB；③△BRP≌△CSP．其中正确的是（ ）
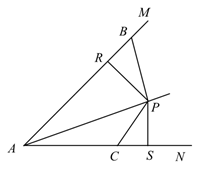A、①② B、②③ C、①③ D、①②③二、填空题
-
9. 已知△ABC的两条边长分别为2和5，则第三边c的取值范围是.10. 如图， ， ， ，则 .
11. 如图，在△ABD和△ACE中，有下列四个判断：①AB=AC；②AD=AE；③∠B=∠C；④BD=CE ， 请以其中三个判断为条件，另一个为结果，写出一个正确的结论(用序号⊗⊗⊗⇒⊗形式写出)．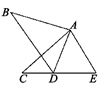
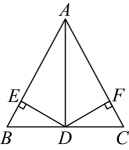
12. 如图，已知 ，若 ， ，则 度．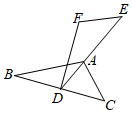
13. 如图，在△ABC中，AB＝BC，BE平分∠ABC，AD为BC边上的高，且AD＝BD．则∠3＝°．
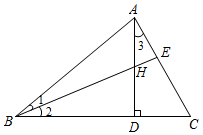14. 如图，在 中， ， 为 边 上一点， ， 平分 的外角，且 .连接 交 于 为边 上一点，满足 ，连接 交 于H.以下结论：① ；② ；③ ；④若 平分 ，则 平分 正确的是.
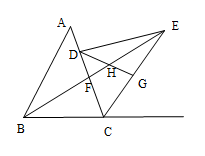15. 如图，在△ABC中，AB＝AC＝24厘米，∠B=∠C ，BC＝16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为厘米/秒时，能够在某一时刻使△BPD与△CQP全等．
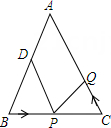16. 如图，∠A＝∠B＝90°，AB＝60，E，F 分别为线段 AB 和射线 BD 上的一点，若点 E 从点 B 出发向点 A 运动，同时点 F 从点 B 出发向点 D 运动，二者速度之比为 3：7，运动到某时刻同时停止，在射线 AC 上取一点 G，使△AEG 与△BEF 全等，则 AG 的长为.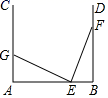
三、解答题
-
17. 已知：如图，AB ＝ AD．请添加一个条件使得△ABC≌△ADC，然后再加以证明．
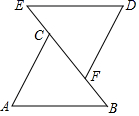
18. 如图，已知△ABD≌△ACE．求证：BE=CD．
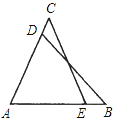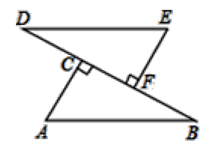
19. 证明题已知：如图，点A、F、C、D在同一条直线上，AB∥DE ， AB=DE ， AF=DC ．
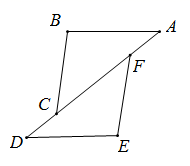
求证：BC=EF ．
20. 如图，已知△ABC≌△DEF，∠A＝85°，∠B＝60°，AB＝8，EH＝2.求∠F的度数与DH的长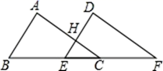
21. 如图，要测量河岸相对两点A，B的距离，可以从AB的垂线BF上取两点C，D，使 过点D作 ，且A，C，E三点在一直线上.若测得 米，即可知道AB也为15米.请说明理由.
