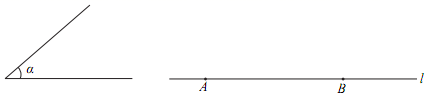初中数学北师大版七年级下学期 第四章 4.4 用尺规作三角形
试卷更新日期:2021-04-13 类型:同步测试
一、单选题
-
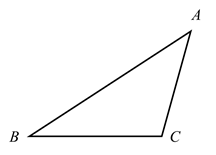
1. 如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有( )
 A、6个 B、7个 C、8个 D、9个2. 如图,已知一条线段的长度为a,作边长为a的等边三角形的方法是:①画射线AM;②连结AC、BC;③分别以A、B为圆心,以a的长为半径作圆弧,两弧交于点C;④在射线AM上截取AB=a;以上画法正确的顺序是( )
A、6个 B、7个 C、8个 D、9个2. 如图,已知一条线段的长度为a,作边长为a的等边三角形的方法是:①画射线AM;②连结AC、BC;③分别以A、B为圆心,以a的长为半径作圆弧,两弧交于点C;④在射线AM上截取AB=a;以上画法正确的顺序是( )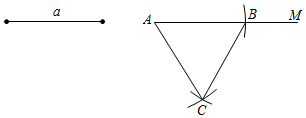 A、①②③④ B、①④③② C、①④②③ D、②①④③3. 用尺规作图,下列条件中可能作出两个三角形的是( )A、已知两边和夹角 B、已知两边及其一边的对角 C、已知两角和夹边 D、已知三条边4. 如图,已知线段a,h作等腰△ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连接AB,AC,△ABC为所求的等腰三角形.上述作法的四个步骤中,有错误的一步你认为是( )
A、①②③④ B、①④③② C、①④②③ D、②①④③3. 用尺规作图,下列条件中可能作出两个三角形的是( )A、已知两边和夹角 B、已知两边及其一边的对角 C、已知两角和夹边 D、已知三条边4. 如图,已知线段a,h作等腰△ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连接AB,AC,△ABC为所求的等腰三角形.上述作法的四个步骤中,有错误的一步你认为是( )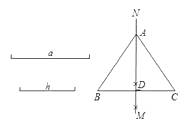 A、(1) B、(2) C、(3) D、(4)5. 如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
A、(1) B、(2) C、(3) D、(4)5. 如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )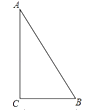 A、4 B、5 C、6 D、76. 如图,在 中, ,以 的一边为边画等腰三角形,使得它的第三个顶点在 的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
A、4 B、5 C、6 D、76. 如图,在 中, ,以 的一边为边画等腰三角形,使得它的第三个顶点在 的其他边上,则可以画出的不同的等腰三角形的个数最多为( )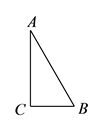 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 如下框内是“已知一条直角边和斜边作直角三角形”的尺规作图过程.
已知:线段a、b,
求作: 使得斜边 , .
作法:如图.
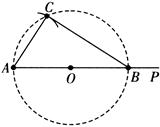
作射线AP,截取线段 ;
以AB为直径,作 ;
以点A为圆心,a的长为半径作弧交 于点C;
连接AC、CB.
即为所求作的直角三角形.
请您写出上述尺规作图的依据:.
8. 如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画出个.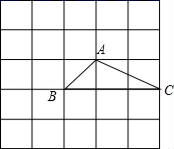 9. 如图,∠EAD为锐角,C是射线AE上一点,点B在射线AD上运动(点A与点B不重合),设点C到AD的距离为d,BC长度为a,AC长度为b,在点B运动过程中,b、d保持不变,当a满足条件时,△ABC唯一确定.
9. 如图,∠EAD为锐角,C是射线AE上一点,点B在射线AD上运动(点A与点B不重合),设点C到AD的距离为d,BC长度为a,AC长度为b,在点B运动过程中,b、d保持不变,当a满足条件时,△ABC唯一确定. 10. 已知线段a,b,c,求作 ,使 , , ,下面作法的合理顺序为(填序号)
10. 已知线段a,b,c,求作 ,使 , , ,下面作法的合理顺序为(填序号)①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;
②作直线 ,在 上截取 ;
③连接 , , 为所求作的三角形.
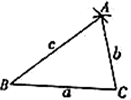 11. 如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出个.
11. 如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出个.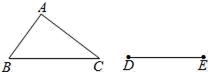 12. 用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是 .
12. 用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是 .三、解答题
-
13. 如图,已知 ,用直尺和圆规作 ,使得 .
 14. 在 的方格中, 的三个顶点都在格点上,我们把像这种顶点在格点的三角形叫格点三角形,请按要求完成下列作图
14. 在 的方格中, 的三个顶点都在格点上,我们把像这种顶点在格点的三角形叫格点三角形,请按要求完成下列作图 (1)、在图1的方格中作出与 相似的最小格点三角形.(2)、在图2中把线段AC分成三条相等的线段 ,点E,F都在线段AC上.
(1)、在图1的方格中作出与 相似的最小格点三角形.(2)、在图2中把线段AC分成三条相等的线段 ,点E,F都在线段AC上.(①只能用无刻度的直尺作直线;②保留作图痕迹)