浙江省宁波市北仑区2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-08 类型:期末考试
一、单选题
-
1. 若 ,则下列比例式成立的是( )A、 B、 C、 D、2. 如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转 后,能与原图形完全重合的是( )A、
 B、
B、 C、
C、 D、
D、 3. “小明过学校门口的马路遇到红灯”这个事件是( )A、确定事件 B、不确定事件 C、不可能事件 D、必然事件4. 正十边形的每个内角都是( )A、 B、 C、 D、5. 在 中, ,则 的值是( )A、 B、 C、 D、6. 若 的半径 ,点O到直线 的距离为3,下列图中位置关系正确的是( )A、
3. “小明过学校门口的马路遇到红灯”这个事件是( )A、确定事件 B、不确定事件 C、不可能事件 D、必然事件4. 正十边形的每个内角都是( )A、 B、 C、 D、5. 在 中, ,则 的值是( )A、 B、 C、 D、6. 若 的半径 ,点O到直线 的距离为3,下列图中位置关系正确的是( )A、 B、
B、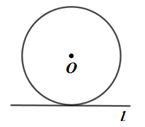 C、
C、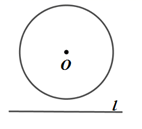 D、
D、 7. 二次函数 经过适当变换之后得到新的二次函数 ,则这个变换为( )A、向上5个单位,向右3个单位 B、向下5个单位,向右3个单位 C、向上5个单位,向左3个单位 D、向下5个单位,向左3个单位8. 如图, 过点 ,点C是 上的一点,连接 ,则 的度数为( )
7. 二次函数 经过适当变换之后得到新的二次函数 ,则这个变换为( )A、向上5个单位,向右3个单位 B、向下5个单位,向右3个单位 C、向上5个单位,向左3个单位 D、向下5个单位,向左3个单位8. 如图, 过点 ,点C是 上的一点,连接 ,则 的度数为( ) A、 B、 C、 D、9. 如图,在平面直角坐标系 中,函数 的图像与对称轴直线 交于点A,与 轴交于 三点,下列命题正确的是( )
A、 B、 C、 D、9. 如图,在平面直角坐标系 中,函数 的图像与对称轴直线 交于点A,与 轴交于 三点,下列命题正确的是( )① ;②若 ,则 ;③对于任意 ,始终有 ;④若B的坐标为 ,则C的坐标为 .
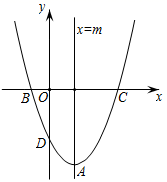 A、①②③ B、①②④ C、①③④ D、②③④10. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图,以直角三角形的各边为边分别向外作正三角形,再把较小的两张正三角形纸片按图的方式放置在最大正三角形内.若知道图中阴影部分的面积,则一定能求出( )
A、①②③ B、①②④ C、①③④ D、②③④10. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图,以直角三角形的各边为边分别向外作正三角形,再把较小的两张正三角形纸片按图的方式放置在最大正三角形内.若知道图中阴影部分的面积,则一定能求出( ) A、直角三角形的面积 B、最大正三角形的面积 C、较小两个正三角形重叠部分的面积 D、最大正三角形与直角三角形的面积和
A、直角三角形的面积 B、最大正三角形的面积 C、较小两个正三角形重叠部分的面积 D、最大正三角形与直角三角形的面积和二、填空题
-
11. 在半径为2的圆中,圆心角为 的扇形面积为.12. 如图,四边形 内接于 ,若 , .
 13. 在一个不透明的口袋里装有仅颜色不同100个球,某小组做摸球实验,将球搅匀后从中随机摸出1个球,记下颜色,再把它放回,不断重复,下表是实验中记下的一组数据:
13. 在一个不透明的口袋里装有仅颜色不同100个球,某小组做摸球实验,将球搅匀后从中随机摸出1个球,记下颜色,再把它放回,不断重复,下表是实验中记下的一组数据:摸球的次数n
100
150
200
500
800
1000
摸到红球的次数m
79
115
152
385
598
751
摸到红球的频率
0.790
0.767
0.760
0.770
0.748
0.751
试估计口袋中红球有个.
14. 在“测量学校教学楼的高度”的数学活动中,小刚同学使用镜面反射法进行测量,如图所示.若 米, 米, 米,则这个学校教学楼的高度为米. 15. 如图,点B是 的半径 上的中点,过点B作 的垂线交 于点 是 上一点, ,过点C作 的切线l,连接 并延长交直线l于点F.已知 的半径为4,则 为 .
15. 如图,点B是 的半径 上的中点,过点B作 的垂线交 于点 是 上一点, ,过点C作 的切线l,连接 并延长交直线l于点F.已知 的半径为4,则 为 . 16. 如图,在平面直角坐标系中,二次函数 与y轴,x轴相交于 三点,D是函数的顶点,M是第四象限内一动点,且 ,连接 ,则 的最小值是 .
16. 如图,在平面直角坐标系中,二次函数 与y轴,x轴相交于 三点,D是函数的顶点,M是第四象限内一动点,且 ,连接 ,则 的最小值是 .
三、解答题
-
17. “青年北仑”建设是北仑建设的一大亮点,现将质地大小完全相同,上面标有“青”“年”“北”“仑”字样的四个彩球放入同一个袋子.(1)、小慧在袋子中随机摸出一个彩球,记下字样后放回,搅匀,再摸出一个彩球,请用列表或画树状图的方法,写出所有的可能;(2)、在(1)的条件下能拼出“北仑”(不分先后)的概率是多少?18. 图1、图2均是 的正方形网格,每个小正方形的顶点称为格点,线段 的端点均在格点上,回答下列问题:
 (1)、在图1中, , ;(2)、在图2中请用一把无刻度的尺子,画出线段 三等分点 .(保留作图痕迹)19. 已知抛物线 经过点 .(1)、求a的值;(2)、若点 都在该抛物线上,试比较 与 的大小.20. 如图,富邦城即将建造一个大型摩天轮,工程师介绍若你站在距离摩天轮40米处(A点),以 的仰角恰好可以看到摩天轮圆轮的底部(C点),以 的仰角可以看到摩天轮圆轮的最上方(D点).(人的身高忽略不计)(参考数据: )
(1)、在图1中, , ;(2)、在图2中请用一把无刻度的尺子,画出线段 三等分点 .(保留作图痕迹)19. 已知抛物线 经过点 .(1)、求a的值;(2)、若点 都在该抛物线上,试比较 与 的大小.20. 如图,富邦城即将建造一个大型摩天轮,工程师介绍若你站在距离摩天轮40米处(A点),以 的仰角恰好可以看到摩天轮圆轮的底部(C点),以 的仰角可以看到摩天轮圆轮的最上方(D点).(人的身高忽略不计)(参考数据: ) (1)、求摩天轮的底部(C点)到地面(B点)的距离;(精确到个位)(2)、求摩天轮的圆轮直径(即 ).(精确到个位)21. 如图,已知 是 斜边 上的中线,过点D作 的平行线,过点C作 的垂线,两线相交于点E.
(1)、求摩天轮的底部(C点)到地面(B点)的距离;(精确到个位)(2)、求摩天轮的圆轮直径(即 ).(精确到个位)21. 如图,已知 是 斜边 上的中线,过点D作 的平行线,过点C作 的垂线,两线相交于点E. (1)、求证: ;(2)、若 ,求 的面积.22. 科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如表):
(1)、求证: ;(2)、若 ,求 的面积.22. 科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如表):温度
……
0
2
4
4.5
……
植物每天高度增长量
……
41
49
49
41
25
19.75
……
由这些数据,科学家推测出植物每天高度增长量 是温度 的函数,且这种函数是一次函数和二次函数中的一种.
(1)、请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外一种函数的理由;(2)、如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过 ,那么实验室的温度 应该在哪个范围内选择?请说明理由.23. 如图, 是 的直径, 为 上一点,过点C的直线交 的延长线于点 平分 ,过点A作 于点 与 交于点E. (1)、求证: 是 的切线;(2)、若 ,
(1)、求证: 是 的切线;(2)、若 ,①求 的长;
②求 的长.
24. 在平面直角坐标系 中, 的半径为1, 为 外两点, .给出如下定义:平移线段 ,得到 的弦 ( 分别为点 的对应点),线段 长度的最小值称为线段 到 的“平移距离”.
 (1)、如图,平移线段 得到 的长度为 的弦 和 ,则这两条弦的位置关系是;在点 中,连接点A与点的线段的长度等于线段 到 的“平移距离”;(2)、若点A在直线 上;
(1)、如图,平移线段 得到 的长度为 的弦 和 ,则这两条弦的位置关系是;在点 中,连接点A与点的线段的长度等于线段 到 的“平移距离”;(2)、若点A在直线 上;①若点B也在直线 上,记线段 到 的“平移距离”为 ,求 的最小值;
②若点B在抛物线 上且 轴,是否存在这样的点B满足题意,若存在,求出“平移距离”为 的最小值,若不存在,说明理由;
(3)、若点A的坐标为 ,记线段 到 的“平移距离”为 ,则 的取值范围为 , 当 取最小值时点B的坐标为 .