江苏省无锡市宜兴市2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-08 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程x²=1的解是（　　）

A、x=1 B、x=﹣1 C、x=±1 D、x=0

查看试题解析
2. 下列方程中，有两个相等实数根的是（）

A、 $x^{2} + 1 = 2 x$ B、 $x^{2} + 1=0$ C、 $x^{2} - 2 x = 3$ D、 $x^{2} - 2 x = 0$

查看试题解析
3. 冉冉的妈妈在网上销售装饰品．最近一周，每天销售某种装饰品的个数为：.11，10，11，13，11，13，15关于这组数据，冉冉得出如下结果，其中错误的是（）

A、众数是11 B、平均数是12 C、方差是 $\frac{18}{7}$ D、中位数是13

查看试题解析
4. 目前以 $5 G$ 等为代表的战略性新兴产业蓬勃发展.某市2019年底有 $5 G$ 用户2万户，计划到2021年底全市 $5 G$ 用户数累计达到8.72万户.设全市 $5 G$ 用户数年平均增长率为 $x$ ，则 $x$ 值为（）

A、 $20 %$ B、 $30 %$ C、 $40 %$ D、 $50 %$

查看试题解析
5. 二次函数y=x²的图象平移后经过点（2，0），则下列平移方法正确的是（　　）

A、向左平移2个单位，向下平移2个单位 B、向左平移1个单位，向上平移2个单位 C、向右平移1个单位，向下平移1个单位 D、向右平移2个单位，向上平移1个单位

查看试题解析
6. 如图，AB是半圆的直径，O是圆心，C是半圆上的点，D是 $\overset{⌢}{A C}$ 上的点，若∠BOC ＝ 50°，则∠D的大小为（）

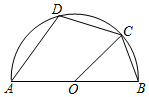A、100° B、105° C、110° D、115°

查看试题解析
7. 已知点 $A ， B ， C$ 在 $⊙ O$ 上．则下列命题为真命题的是（）

A、若半径 $O B$ 平分弦 $A C$ ．则四边形 $O A B C$ 是平行四边形 B、若四边形 $O A B C$ 是平行四边形．则 $∠ A B C = 120 °$ C、若 $∠ A B C = 120 °$ ．则弦 $A C$ 平分半径 $O B$ D、若弦 $A C$ 平分半径 $O B$ ．则半径 $O B$ 平分弦 $A C$

查看试题解析
8. 如图，在半径为1的⊙O中，将劣弧AB沿弦AB 翻折，使折叠后的 $\overset{⌢}{A B}$ 恰好与OB、OA相切，则劣弧AB的长为（）

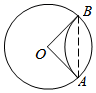A、 $\frac{1}{2} π$ B、 $\frac{1}{3} π$ C、 $\frac{1}{4} π$ D、 $\frac{1}{6} π$

查看试题解析
9. 如图，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平后再次折叠，使点A落在EF上的点A' 处，得到折痕BM，且BM与EF相交于点N，若直线BA'交直线CD于点O，BC ＝ $5 \sqrt{3}$ ，EN ＝ $\sqrt{3}$ ，则OD的长为（）

A、 $\frac{3}{2}$ B、1 C、 $\frac{3}{4}$ D、 $\frac{3}{5}$

查看试题解析
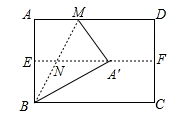10. 如图，抛物线 $y = a x^{2} + b x - 8$ 交y轴于点A，交过点A且平行于x轴的直线于另一点B，交x轴于C、D两点（点C在点D的左边），对称轴为直线 $x = - 5$ ，连接BD、AD、BC，若点A关于直线BD的对称点恰好落在线段OC上，下列结论中错误的是（）

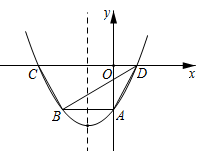A、B的坐标是（－10，－8） B、 $a = \frac{1}{12}$ C、D点坐标为（6，0） D、 $b = \frac{4}{5}$

查看试题解析

二、填空题

11. 已知 $\frac{a}{b} = \frac{c}{d} = \frac{2}{3}$ ，且 $b \neq d$ ，则 $\frac{a - c}{b - d} =$ .

查看试题解析
12. 《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题：直田积八百六十四步，只云阔不及长一十二步．问阔及长各几步？大意是“一个矩形田地的面积等于864平方步，它的宽比长少12步，问长与宽各多少步？”若设矩形田地的宽为x步，则所列方程为．

查看试题解析
13. 菱形的一条对角线长为8，其边长是方程 $x^{2} - 9 x + 20 = 0$ 的一个根，则该菱形的周长为．

查看试题解析
14. 关于x的一元二次方程 $(k - 1) x^{2} + 6 x + k^{2} + k - 2 = 0$ 有一个根是0，则k的值是

查看试题解析
15. 底面半径为6cm的圆锥，将其侧面展开之后所得扇形的圆心角是135°，则此圆锥的母线长为cm

查看试题解析
16. 如图，在边长为3的正六边形ABCDEF中，将四边形ADEF绕点A顺时针旋转到四边形 $A D^{'} E^{'} F^{'}$ 处，此时边 $A D^{'}$ 与对角线AC重叠，则图中阴影部分的面积是.

查看试题解析
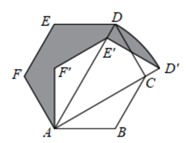17. 如图，在Rt△ABC中，∠C=90°，∠A=30°，点P在AC上，以点P为中心，将△ABC顺时针旋转90°，得到△DEF，DE交边AC于G，当P为DF中点时，AG：DG的值为

查看试题解析
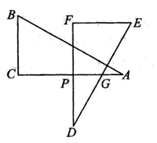18. 如图，在矩形ABCD中，CD是⊙O直径，E是BC的中点，P是直线AE上任意一点，AB＝4，BC＝6，PM、PN相切于点M、N，当∠MPN最大时，PM的长为.

查看试题解析

三、解答题

19. 解方程

(1)、 $x^{2} + 4 x - 2 = 0$

(2)、 $2 x (x - 3) = x - 3$

查看试题解析
20. 如图，D、E分别在AB、AC上，∠AED=∠B，AB=6，BC=5，AE=4

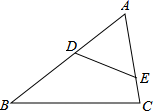(1)、求DE的长；

(2)、若四边形BCED的面积为6，求 $△ A B C$ 的面积

查看试题解析
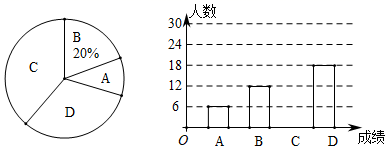21. 某中学全校学生参加了“交通法规”知识竞赛，为了解全校学生竞赛成绩的情况，随机抽取了一部分学生的成绩，分成四组：A： $60 \leq x < 70$ ；B： $70 \leq x < 80$ ；C： $80 \leq x < 90$ ；D： $90 \leq x \leq 100$

(1)、请将条形统计图补充完整；

(2)、在扇形统计图中，计算出D： $90 \leq x \leq 100$ 这一组对应的圆心角是度；

(3)、所抽取学生成绩的中位数在哪个组内，并说明理由；

(4)、若该学校有1500名学生，估计这次竞赛成绩在A： $60 \leq x < 70$ 组的学生有多少人？

查看试题解析
22. 在一个不透明的布袋里装有3个大小、质地均相同的乒乓球，球上分别标有数字为1、2、3

(1)、随机从布袋中一次摸出两个乒乓球，写出两个乒乓球上的数字都是奇数的概率是；

(2)、随机从布袋中摸出一个乒乓球，记下数字后放回布袋里，再随机从布袋中摸出一个乒乓球，请用列表或画树状图的方法求出两个乒乓球上的数字之和不小于4的概率.

查看试题解析
23. 如图，在一次高尔夫球的比赛中，某运动员在原点O处击球，目标是离击球点10米远的球洞，球的飞行路线是一条抛物线，结果球的落地点距离球洞2米，（击球点、落地点、球洞三点共线）球在空中最高处达3.2米.

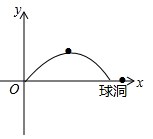(1)、求表示球飞行的高度y（单位：米）与表示球飞出的水平距离x（单位：米）之间的函数关系式；

(2)、当球的飞行高度不低于3米时，求x的取值范围.

查看试题解析
24. 在△ABC中，∠ACB=90°，点E、F分别是边AB、BC上的两个点，点B关于直线EF的对称点P恰好落在边AC上且满足EP⊥AC.

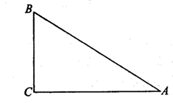(1)、请你利用无刻度的直尺和圆规画出对称轴EF；（保留作图痕迹，不写作法）

(2)、若BC=3，AC=4，则四边形BEPF的周长= ，线段EF=

查看试题解析
25. 如图，AB是⊙O的直径，CD是⊙O的切线，C在AB的延长线上.

(1)、求证：△CAD∽△CDB

(2)、若∠C＝30°，AC＝9，求△DBC的面积

查看试题解析
26. 某公司生产的商品的市场指导价为每件500元，公司的实际销售价格可以浮动x个百分点，即销售价格=500（1+x%），经过市场调研发现，这种商品的日销售量y（件）与销售价格浮动的百分点x之间的函数关系为y=-10x+120，若该公司按浮动-12个百分点的价格出售，每件商品仍可获利10%.

(1)、求该公司生产销售每件商品的成本为多少元；

(2)、当该公司的商品定价为每件多少元时，日销售利润最多？最多是多少元？（说明：日销售利润=（销售价格-成本）×日销售量）

(3)、该公司决定每销售一件商品就捐赠m元利润（m≥l）给希望工程，公司通过销售记录发现，当价格浮动的百分点大于-3时，扣除捐赠后的日销售利润随x增大而减小，直接写出m的取值范围.

查看试题解析
27. 如图，在矩形ABCD中，AB＝15，E是BC上的一点，将△ABE沿着AE折叠，点B刚好落在CD边上点G处；点F在DG上，将△ADF沿着AF折叠，点D刚好落在AG上点H处，且CE＝ $\frac{4}{5} B E$ ，

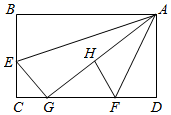(1)、求AD的长；

(2)、求FG的长

查看试题解析
28. 如图，顶点为M的抛物线 $y = m x^{2} - 2 m x + n$ 与x轴交于A、B两点（点A在点B的左边），与y轴的正半轴交于点C，已知 $A (- 2 ， 0)$ ，∠ACO＝30°

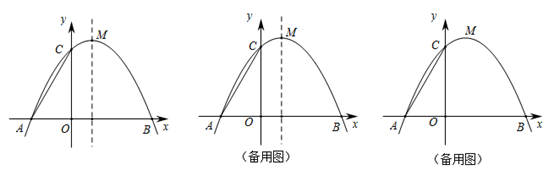(1)、求抛物线的解析式和M的坐标；

(2)、若点N是抛物线的对称轴上的一个动点，且满足△CAN是直角三角形，直接写出点N的坐标；

(3)、已知点G是y轴上的一点，直接写出GC＋2GB的最小值，以及此时点G的坐标.

查看试题解析