江苏省无锡市新吴区2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-08 类型：期末考试

进入出卷网下载

一、单选题

1. $\cos 60 °$ 的值是（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
2. 方程 $x^{2} = 4 x$ 的根是（）

A、 $x = 4$ B、 $x = 0$ C、 $x_{1} = 0$ ， $x_{2} = 4$ D、 $x_{1} = 0$ ， $x_{2} = - 4$

查看试题解析
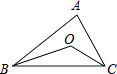
3. 受新冠肺炎疫情影响，某企业生产总值从六月份的500万元，连续两个月降至380万元，设平均下降率为x，则可列方程（）

A、 $500 (1 - x) = 380$ B、 $500 (1 - 2 x) = 380$ C、 $500 {(1 - x)}^{2} = 380$ D、 $500 {(1 + x)}^{2} = 380$

查看试题解析
4. 二次函数 $y = a x^{2} + b x + 2$ 的图象经过点 $(- 1, 0)$ ，则代数式 $a - b$ 的值为（）

A、0 B、 $- 2$ C、 $- 1$ D、2

查看试题解析
5. 某校有25名同学参加比赛，预赛成绩各不相同，要取前12名参加决赛，小颖已经知道了自己的成绩，她想知道自己能否进入决赛，只需再知道这25名同学成绩的（）

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
6. ⊙O的半径为7，圆心O到直线l的距离为6，则直线l与⊙O的位置关系是（）

A、相交 B、相切 C、相离 D、无法确定

查看试题解析
7. 如图，在 $▱ A B C D$ 中，E为BC的中点，DE、AC交于点F，则 $\frac{E F}{D F}$ 的值为（）

A、1 B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
8. 如图，⊙O与正方形ABCD的两边AB.AD都相切，且DE与⊙O相切于点E，若正方形ABCD的边长为4， $D E = 3$ ，则OD的长为（）

A、 $2 \sqrt{2}$ B、 $\sqrt{10}$ C、 $\frac{7}{2}$ D、4

查看试题解析
9. 如图，在Rt△ABC 中，∠ACB=90°，∠A=30°，BC=2．将△ABC绕点C按顺时针方向旋转n度后得到△EDC，此时点D在AB边上，斜边DE交AC边于点F，则n的大小和图中阴影部分的面积分别为（）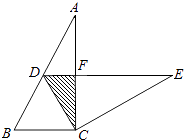

A、30，2 B、60，2 C、60， $\frac{\sqrt{3}}{2}$ D、60， $\sqrt{3}$

查看试题解析
10. 将一个正方形剪成①、②、③、④四块（如图1），恰能拼成如图2的矩形，若 $a = 1$ ，则这个正方形的面积为（）

A、 $\frac{\sqrt{5} + 1}{2}$ B、 $\frac{\sqrt{5} - 1}{2}$ C、9 D、 $\frac{7 + 3 \sqrt{5}}{2}$

查看试题解析

二、填空题

11. 若关于x的一元二次方程x²﹣4x+m=0有两个不相等的实数根，则m的取值范围为．

查看试题解析
12. 已知 $\frac{x}{y} = \frac{2}{3}$ ，则 $\frac{x + y}{y} =$

查看试题解析
13. 若点P是线段AB的黄金分割点， $A B = 10 cm$ ，则较长线段AP的长是cm.（保留根号）

查看试题解析
14.
已知O为△ABC的内心，且∠BOC=130°，则∠A= ．

查看试题解析
15. 已知圆锥的底面圆的半径为 $1$ ，母线长为 $3$ ，其侧面展开图的圆心角是.

查看试题解析
16. 如图，四边形ABCD内接于⊙O，AB是直径， $∠ A B C = 40 °$ ， $O D / / B C$ ，则 $∠ B C D$ 的度数为.

查看试题解析
17. 在平面直角坐标系中，若点 $P (a, b)$ 的坐标满足 $a = b \neq 0$ ，则称点P为“对等点”.已知一个二次函数 $y = x^{2} + 2 m x - m$ 的图象上存在两个不同的“对等点”，且这两个“对等点”关于原点对称，则m的值为.

查看试题解析
18. 如图， $△ A B C$ 的顶点都在正方形网格纸的格点上，则 $\sin \frac{∠ C}{2} =$ .

查看试题解析

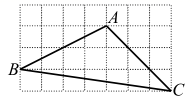
三、解答题

19.

(1)、计算： $2 \tan 60 ° - \sqrt{12} - {(\sqrt{3} - 2)}^{0} + {(\frac{1}{3})}^{- 1}$ ；

(2)、解方程： $x^{2} + 2 x - 2 = 0$ .

查看试题解析
20. 某中学为了了解七年级学生对“垃圾不落地，城市更美丽”这一倡议的落实情况，学校安排德育处在七年级学生中随机抽取了部分学生，并针对学生“是否随手丢垃圾”这一情况进行了问卷调査，统计结果为：A为从不随手丢垃圾；B为偶尔随手丢垃圾；C为经常随手丢垃圾三项.要求每位被调查的学生必须从以上三项中选一项且只能选一项，现将调査结果绘制成以下两幅不完整的统计图.

请你根据以上信息，解答下列问题：

(1)、上述条形统计图和扇形统计图都不完整，请补全；

(2)、所抽取学生“是否随手丢垃圾”情况的众数是落在A，B，C中的；

(3)、若该校七年级共有1500名学生，请你估计该年级学生中“经常随手丢垃圾”的学生约有多少人？

查看试题解析
21. 初三（1）班要从2男2女共4名同学中选人做晨会的升旗手．

(1)、若从这4人中随机选1人，则所选的同学性别为男生的概率是．

(2)、若从这4人中随机选2人，求这2名同学性别相同的概率．

查看试题解析
22. 如图，在 $▱ A B C D$ 中，E是AD上一点，延长CE到点F，使得 $∠ F B C = ∠ D C E$ .

(1)、求证： $∠ D = ∠ F$ ；

(2)、请用无刻度直尺与圆规在AD上求作一点P，使 $∠ B P C = ∠ D$ .（保留作图痕迹，不写作法）

查看试题解析
23. 如图，AB是⊙O的直径，点C在⊙O上， $∠ A B C$ 的平分线与AC相交于点D，与⊙O过点A的切线相交于点E.

(1)、猜想 $△ E A D$ 的形状，并证明你的猜想；

(2)、若 $A B = 4$ ， $A D = 3$ ，求BD的长.

查看试题解析
24. 疫情突发，危难时刻，从决定建造到交付使用，雷神山、火神山医院仅用时十天，其建造速度之快，充分展现了中国基建的巨大威力！这样的速度和动员能力就是全国人民的坚定信心和尽快控制疫情的底气！改革开放 $40$ 年来，中国已经成为领先世界的基建强国，如图①是建筑工地常见的塔吊，其主体部分的平面示意图如图②，点F在线段HG上运动， $B C / / H G ， A E ⊥ B C ，$ 垂足为点 $E ， A E$ 的延长线交HG于点 G，经测量 $∠ A B D ＝ 11 ° ， ∠ A D E ＝ 26 ° ， ∠ A C E ＝ 31 ° ， B C ＝ 20 m$ $， E G ＝ 0.6 m$ ，

(1)、求线段 $A G$ 的长度；（结果精确到 $0.1 m$ ）

(2)、连接AF，当线段 $A F ⊥ A C$ 时，求点F和点G之间的距离.（结果精确到0.1m，参考数据： $t a n 11 ° \approx 0.19 ， t a n 26 ° \approx 0.49 ，$ $t a n 31 ° \approx 0.60$ ）

查看试题解析
25. 社区利用一块矩形空地建了一个小型的便民停车场，其布局如图所示.已知 $A D = 52 m$ ， $A B = 28 m$ ，阴影部分设计为停车位，要铺花砖，其余部分是等宽的通道.已知铺花砖的面积为 $640 m^{2}$ .

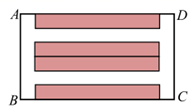(1)、求通道的宽是多少米？

(2)、该停车场共有车位50个，据调查分析，当每个车位的月租金为200元时，可全部租出；当每个车位的月租金每上涨5元，就会少租出1个车位，求停车场的月租金收入最多为多少元？

查看试题解析
26. 如图1，在Rt△ACB中， $∠ A C B = 90 °$ ， $A B = 10$ ， $B C = 6$ ，点D、F分别是边AC、BC上的动点，过点D做AB的垂线，垂足为E，连结FD，FE.设C、D两点之间的距离为x，C、F两点之间的距离为y.

(1)、当 $D E = 4$ 时，求x的值；

(2)、如图2，以FD，FE为邻边作 $▱ F D G E$ ，当 $x = 3$ 时，是否存在y，使得 $▱ F D G E$ 的顶点G恰好落在 $△ A B C$ 的边上？若存在，请求出y的值，若不存在，请说明理由.

查看试题解析
27. 如图，矩形OABC中，点A，点C分别在x轴，y轴上，D为边BC上的一动点，现把 $△ O C D$ 沿OD对折，C点落在点P处，已知点B的坐标为 $(2 \sqrt{3} ， 2)$ .

(1)、当D点坐标为 $(2 ， 2)$ 时，求P点的坐标；

(2)、在点D沿BC从点C运动至点B的过程中，设点P经过的路径长度为 $l$ ，求 $l$ 的值；

(3)、在点D沿BC从点C运动至点B的过程中，若点P落在同一条直线 $y = k x + 4$ 上的次数为2次，请直接写出k的取值范围.

查看试题解析
28. 如图，在平面直角坐标系中，已知抛物线 $y = a x^{2} + b x - 8$ 与x轴交于A，B两点，与y轴交于点C，直线l经过坐标原点O，与抛物线的一个交点为D，与抛物线的对称轴交于点E，连接CE，已知点A，D的坐标分别为 $(- 2 ， 0)$ ， $(6 ， - 8)$ .

(1)、求抛物线的函数表达式；

(2)、试探究抛物线上是否存在点F，使 $△ F O E ≌ △ F C E$ ？若存在，请直接写出点F的坐标；若不存在，请说明理由；

(3)、若点P是y轴负半轴上的一个动点，设其坐标为 $(0 ， m)$ ，直线PB与直线l交于点Q，试探究：当m为何值时， $△ O P Q$ 是等腰三角形.

查看试题解析