江苏省连云港市海州区2021届九年级上学期数学期末考试试

试卷更新日期：2021-04-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（）

A、 $x - 2 = 0$ B、 $x y + 1 = 0$ C、 $x^{2} - 2 x - 3$ D、 $x^{2} - 4 x - 1 = 0$

查看试题解析
2. 已知点P是线段 $A B$ 的黄金分割点（ $A P > P B$ ）， $A B = 2$ ，那么 $A P$ 的长约为（）

A、0.618 B、1.382 C、1.236 D、0.764

查看试题解析
3. 有19位同学参加歌咏比赛，所得的分数互不相同，取得分前10位的同学进入决赛，某同学知道自己的分数后，要判断自己能否进入决赛，他只需知道这19位同学分数的（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
4. 抛物线 $y = k x^{2} - 7 x - 7$ 的图象和x轴有交点，则k的取值范围是（）

A、 $k \geq - \frac{7}{4}$ B、 $k \geq - \frac{7}{4}$ 且 $k \neq 0$ C、 $k > - \frac{7}{4}$ D、 $k > - \frac{7}{4}$ 且 $k \neq 0$

查看试题解析
5. 如图， $A B$ 是 $⊙ O$ 的弦， $A C$ 是 $⊙ O$ 的切线，A为切点， $B C$ 经过圆心，若 $∠ B = 25 °$ ，则 $∠ C$ 的大小等于（）

A、 $40 °$ B、 $45 °$ C、 $50 °$ D、 $65 °$

查看试题解析
6. 如图，在△ABC中，DE∥BC， $\frac{A D}{A B} = \frac{1}{3}$ ，则下列结论中正确的是（）

A、 $\frac{A E}{E C} = \frac{1}{3}$ B、 $\frac{D E}{B C} = \frac{1}{2}$ C、 $\frac{△ A D E 的周长}{△ A B C 的周长} = \frac{1}{3}$ D、 $\frac{△ A D E 的面积}{△ A B C 的面积} = \frac{1}{3}$

查看试题解析
7.
如图，已知△ABC和△ADE均为等边三角形，D在BC上，DE与AC相交于点F，AB=9，BD=3，则CF等于（　　）

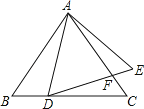A、1 B、2 C、3 D、4

查看试题解析
8. 如图所示，已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与x轴交于 $(x_{1} ， 0)$ ，且 $- 1 < x_{1} < 0$ ，对称轴 $x = 1$ .有下列5个结论：① $a b c > 0$ ；② $b < a + c$ ；③ $4 a + 2 b + c > 0$ ；④ $2 c > 3 b$ ；⑤ $a + b > m (a m + b)$ （ $m$ 是不等于1的实数）.其中结论正确个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 若 $\frac{y}{x} = \frac{3}{4}$ ，则 $\frac{x + y}{x}$ 的值为.

查看试题解析
10. 如图，要使△ACD∽△ABC，只需添加条件(只要写出一种合适的条件即可).

查看试题解析
11. 将二次函数 $y = x^{2}$ 的图象向右平移3个单位，再向上平移4个单位后，所得图象的函数表达式是.

查看试题解析
12. 如图，四边形 $A B C D$ 与四边形 $E F G H$ 位似，位似中心点是O， $\frac{O E}{E A} = \frac{3}{2}$ ，则 $\frac{F G}{B C} =$ .

查看试题解析
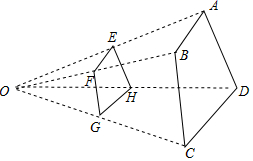13. 如图，圆锥的底面半径为1cm，高SO等于2 $\sqrt{2}$ cm，则侧面展开图扇形的圆心角为°.

查看试题解析
14. 经过两次连续降价，某药品销售单价由原来的50元降到32元，设该药品平均每次降价的百分率为x，根据题意可列方程是．

查看试题解析
15. 王翔同学在一次跳高训练中采用了背跃式，跳跃路线正好和抛物线 $y = - \frac{3}{5} x^{2} + \frac{6}{5} x + 1$ 相吻合，那么他能跳过的最大高度为m.

查看试题解析
16. 如图，已知点A（6，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y₁和过P、A两点的二次函数y₂的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD=AD=5时，这两个二次函数的最大值之和等于。

查看试题解析

三、解答题

17. 解方程： $x^{2} - 2x - 1 = 0$

查看试题解析
18. 已知Rt△ABC的三边长为 $a 、 b 、 c$ ，且关于x的一元二次方程 $x^{2} + (b - 2) x + b - 3 = 0$ 有两个相等的实数根.

(1)、求b的值

(2)、若 $a = 3$ ，求c的值.

查看试题解析
19. 已知二次函数 $y_{1} = x^{2} - 2 x - 3$ 的图象与x轴交于A、B两点（A在B的左侧），与y轴交于点C，顶点为D.

(1)、求点A、B、D的坐标，并在下面直角坐标系中画出该二次函数的大致图象；

(2)、设一次函数 $y_{2} = k x + b (k \neq 0)$ 的图象经过B、C两点，请直接写出满足 $y_{1} < y_{2}$ 的x的取值范围.

查看试题解析
20. 防疫期间，全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道，某天早晨，该校小明和小丽两位同学将随机通过测温通道进入校园.

(1)、小明从A测温通道通过的概率是；

(2)、利用画树状图或列表的方法，求小明和小丽从同一个测温通道通过的概率.

查看试题解析
21. 如图，隧道的截面由抛物线 $A E D$ 和矩形 $A B C D$ 构成，矩形的长 $B C$ 为 $8 m$ ，宽 $A B$ 为 $2 m$ ，隧道最高点E距离地面 $6 m$ ，以 $B C$ 所在的直线为x轴，线段 $B C$ 的垂直平分线为y轴，建立平面直角坐标系，y轴是抛物线的对称轴.

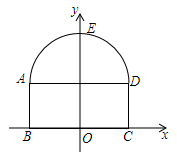(1)、求该抛物线的关系式；

(2)、现有一辆货运卡车高 $4.5 m$ ，宽 $2.4 m$ ，这辆货运卡车能否通过该隧道？通过计算说明你的结论.

查看试题解析
22. 如图，在矩形ABCD中，AB=4，BC=6，M是BC的中点，DE⊥AM于点E．

(1)、求证：△ADE∽△MAB；

(2)、求DE的长．

查看试题解析
23. 某汽车出租公司以每辆汽车月租费3000元，100辆汽车可以全部租出.若每辆汽车的月租费每增加50元，则将少租1辆汽车.已知每辆租出的汽车支付月维护费200元，问每月租出多少辆汽车时，该出租公司的月收益最大？最大月收益是多少？

查看试题解析
24. 如图，在Rt△ABC中，∠ACB=90°，以斜边AB上一点O为圆心，OB为半径作⊙O，交AC于点E，交AB于点D，且∠BEC=∠BDE.

(1)、求证：AC是⊙O的切线；

(2)、连接OC交BE于点F，若 $\frac{C E}{A E} = \frac{2}{3}$ ，求 $\frac{O F}{C F}$ 的值.

查看试题解析
25. 已知：如图①，在 $R t △ A B C$ 中， $A B ⊥ A C$ ， $A B = 6 cm$ ， $B C = 10 cm$ ，将 $△ A B C$ 绕 $A C$ 中点旋转 $180 °$ 得到 $△ C D A$ .如图②，再将 $△ C D A$ 沿 $A C$ 的方向以 $1 cm/s$ 的速度平移得到 $△ N D P$ ；同时，点Q从点C出发，沿 $C B$ 方向以 $2 cm/s$ 的速度运动，当点Q停止运动时， $△ N D P$ 也停止平移，设运动时间为 $t (s) (0 < t < 5)$ .解答下列问题.

(1)、当t为何值时， $P Q / / A B$ ？

(2)、在运动过程中，t为何值时 $△ P Q C$ 的面积最大？并求面积的最大值；

(3)、是否存在某一时刻t，使 $P Q ⊥ D Q$ ？若存在，请求出t的值；若不存在，请说明理由.

查看试题解析
26. 已知抛物线 $y = a x^{2} + b x + 3$ 与x轴交于点 $A (- 1 ， 0)$ ，点 $B (3 ， 0)$ ，与y轴交于点C，顶点为点D.

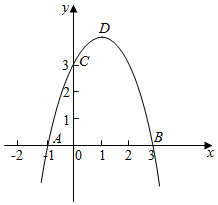(1)、求抛物线的解析式；

(2)、若点P在抛物线上，点Q在x轴上，当以点A、C、P、Q为顶点的四边形是平行四边形时，请直接写出点P的坐标；

(3)、已知点 $H (0 ， \frac{45}{8})$ ， $G (2 ， 0)$ ，在抛物线对称轴上，找一点F，使 $H F + A F$ 的值最小.此时，在抛物线上是否存在一点K，使 $K F + K G$ 的值最小？若存在，求出点K的坐标；若不存在，请说明理由.

查看试题解析