湖南省株洲市茶陵县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-08 类型:期末考试
一、单选题
-
1. 下列各点中,在反比例函数 图象上的是( )A、 B、 C、 D、2. 一元二次方程 的二次项系数、一次项系数和常数项分别是( )A、3, ,9 B、3, , C、3,5,9 D、3,5,3. 如图,在 中, ,且 ,则 的值为( ).
 A、 B、 C、 D、4. 如图,点P在反比例函数y= 的图象上,PA⊥x轴于点A,PB⊥y轴于点B,且△APB的面积为2,则k等于( )
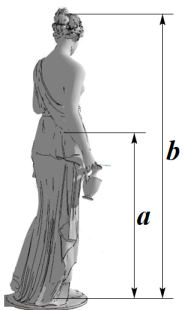
A、 B、 C、 D、4. 如图,点P在反比例函数y= 的图象上,PA⊥x轴于点A,PB⊥y轴于点B,且△APB的面积为2,则k等于( ) A、-4 B、-2 C、2 D、45. 生活中到处可见黄金分割的美,如图,在设计人体雕像时,使雕像的腰部以下a与全身 的高度比值接近0.618,可以增加视觉美感,若图中 为2米,则a约为( )
A、-4 B、-2 C、2 D、45. 生活中到处可见黄金分割的美,如图,在设计人体雕像时,使雕像的腰部以下a与全身 的高度比值接近0.618,可以增加视觉美感,若图中 为2米,则a约为( )
 A、1.24米 B、1.38米 C、1.42米 D、1.62米6. 方程x2=x的解为( )A、x=1 B、x=±1 C、x=0或1 D、x=07. 把函数 与 的图象画在同一个直角坐标系中,正确的是( )A、
A、1.24米 B、1.38米 C、1.42米 D、1.62米6. 方程x2=x的解为( )A、x=1 B、x=±1 C、x=0或1 D、x=07. 把函数 与 的图象画在同一个直角坐标系中,正确的是( )A、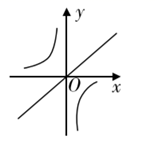 B、
B、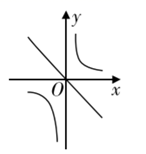 C、
C、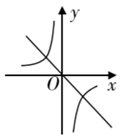 D、
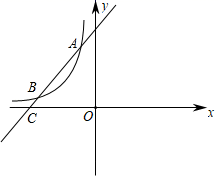
D、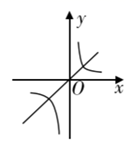 8. 如图,是一条抛物线的图象,则其解析式为( )
8. 如图,是一条抛物线的图象,则其解析式为( )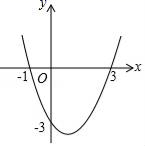 A、y=x2﹣2x+3 B、y=x2﹣2x﹣3 C、y=x2+2x+3 D、y=x2+2x-39. 如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A、y=x2﹣2x+3 B、y=x2﹣2x﹣3 C、y=x2+2x+3 D、y=x2+2x-39. 如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )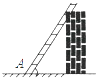 A、sinA的值越小,梯子越陡 B、cosA的值越小,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的函数值无关10. 点P1(﹣1,y1),P2(3,y2),P3(5,y3)均在二次函数y=﹣x2+2x﹣1的图象上,则y1 , y2 , y3的大小关系是( )A、y1=y2>y3 B、y3>y1=y2 C、y1>y2>y3 D、y1<y2<y3
A、sinA的值越小,梯子越陡 B、cosA的值越小,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的函数值无关10. 点P1(﹣1,y1),P2(3,y2),P3(5,y3)均在二次函数y=﹣x2+2x﹣1的图象上,则y1 , y2 , y3的大小关系是( )A、y1=y2>y3 B、y3>y1=y2 C、y1>y2>y3 D、y1<y2<y3二、填空题
-
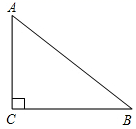
11. 若线段a,b,c,d成比例线段,且a=1cm,b=2cm,c=3cm,则d的长度是cm.12. 若方程 的一个根是 ,则k的值是.13. 已知△ABC∽△A′B′C′,AD和A′D′是对应高,且AD:A′D′=2,则△ABC与△A′B′C′的周长比是.14. 当m时,函数y= 的图象在第二、四象限内.15. 一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下颜色后再放回口袋中.不断重复这一过程,共摸了100次球,发现有70次摸到红球.请你估计这个口袋中红球的数量是.16. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=6,则sinB等于 .
 17. 如图,∠DBC=30°,AB=DB,利用此图求tan75°= .
17. 如图,∠DBC=30°,AB=DB,利用此图求tan75°= .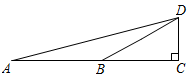 18. 边长为4的正方形ABCD,在BC边上取一动点E,连接AE,作EF⊥AE,交CD边于点F,若CF的长为 ,则CE的长为 .
18. 边长为4的正方形ABCD,在BC边上取一动点E,连接AE,作EF⊥AE,交CD边于点F,若CF的长为 ,则CE的长为 .
三、解答题
-
19. 计算:2cos245°+tan60°•tan30°﹣cos60°20. 已知x1 , x2是一元二次方程x2-3x-1=0的两根,不解方程求下列各式的值:(1)、(2)、21. 某中学开展主题为“垃圾分类知多少”的调查活动,调查问卷设置了“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,要求每名学生选且只能选其中一个等级.随机抽取了120名学生的有效问卷,数据整理如下:
等级
非常了解
比较了解
基本了解
不太了解
人数(人)
24
72
18
(1)、求 的值;(2)、若该校有学生1800人,请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有多少人?22. 在矩形 的 边上取一点E,将 沿 翻折,使点C恰好落在 边上点F处.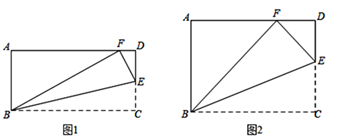 (1)、如图1,若 ,求 的度数;(2)、如图2,当 ,且 时,求 的长;23. 如图,某高速公路设计中需要测量某条江的宽度 ,测量人员使用无人机测量,在 处测得 两点的俯角分别为 和 ,若无人机离地面的高度 为 米,且点 在同一条水平直线上,求这条江的宽度 长(结果保留根号).
(1)、如图1,若 ,求 的度数;(2)、如图2,当 ,且 时,求 的长;23. 如图,某高速公路设计中需要测量某条江的宽度 ,测量人员使用无人机测量,在 处测得 两点的俯角分别为 和 ,若无人机离地面的高度 为 米,且点 在同一条水平直线上,求这条江的宽度 长(结果保留根号).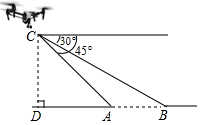 24. 如图1,在△ABC中,∠A=90°,AB=12cm,AC=8cm,现有动点P从点B出发,沿射线BA方向运动,动点Q从点C出发,沿射线CA方向运动,已知点P的速度是2cm/s,点Q的速度是1cm/s,它们同时出发,设运动时间是ts(t>0).
24. 如图1,在△ABC中,∠A=90°,AB=12cm,AC=8cm,现有动点P从点B出发,沿射线BA方向运动,动点Q从点C出发,沿射线CA方向运动,已知点P的速度是2cm/s,点Q的速度是1cm/s,它们同时出发,设运动时间是ts(t>0). (1)、当t=4时,求△APQ的面积.(2)、经过多少秒时,△APQ的面积是△ABC面积的一半.
(1)、当t=4时,求△APQ的面积.(2)、经过多少秒时,△APQ的面积是△ABC面积的一半.