湖北省襄阳市南漳县2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（　　）

A、3x+1＝0 B、x²﹣3＝0 C、y+x²＝4 D、 $\frac{1}{x}$ +x²＝2

查看试题解析
2. 一元二次方程x²＝2x的根是（　　）.

A、0 B、2 C、0和2 D、0和﹣2

查看试题解析
3. 下列方程中，有实数根的是（　　）

A、x²+1＝0 B、4x²﹣4x﹣1＝0 C、3x²+4x+4＝0 D、4x²﹣5x+2＝0

查看试题解析
4. 要得到抛物线y＝2（x﹣4）²+1，可以将抛物线y＝2x²（）

A、向左平移4个单位长度，再向上平移1个单位长度 B、向左平移4个单位长度，再向下平移1个单位长度 C、向右平移4个单位长度，再向上平移1个单位长度 D、向右平移4个单位长度，再向下平移1个单位长度

查看试题解析
5. 在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M₁N₁P₁ ，则其旋转中心可能是（）

A、点A B、点B C、点C D、点D

查看试题解析
6. 在平面直角坐标系中，点 $A (- 2 ， 1)$ 与点 $B$ 关于原点对称，则点 $B$ 的坐标为（）．

A、 $(- 2 ， 1)$ B、 $(2 ， - 1)$ C、 $(2 ， 1)$ D、 $(- 2 ， - 1)$

查看试题解析
7. 如图，⊙O中，弦AB、CD相交于点P，∠A＝40°，∠APD＝75°，则∠B的度数是（）

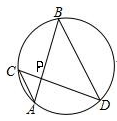A、15° B、40° C、75° D、35°

查看试题解析
8. 下列事件中，属于必然事件的是（　　）

A、2021年阴历正月初一我县是下雨 B、抛一枚硬币，正面朝下 C、购买一张福利彩票中奖了 D、掷一枚骰子，向上一面的数字一定大于零

查看试题解析
9. 半径等于12的圆中，垂直平分半径的弦长为（）

A、 $3 \sqrt{6}$ B、12 $\sqrt{3}$ C、6 $\sqrt{3}$ D、 $18 \sqrt{3}$

查看试题解析
10. 我们定义一种新函数：形如y＝|ax²+bx+c|（a≠0，b²﹣4ac＞0）的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y＝|x²﹣2x﹣3|的图象（如图所示），下列结论错误的是（　　）

A、图象具有对称性，对称轴是直线x＝1 B、当﹣1≤x≤1或x≥3时，函数值y随x值的增大而增大 C、当x＝﹣1或x＝3时，函数最小值是0 D、当x＝1时，函数的最大值是4

查看试题解析

二、填空题

11. 已知关于x的一元二次方程 $x^{2} + x + m = 0$ 的一个根是x=1，那么这个方程的另一个根是．

查看试题解析
12. 解一元二次方程x²＋2x－3＝0时，可转化为解两个一元一次方程，请写出其中的一个一元一次方程.

查看试题解析
13. 事件A发生的概率为 $\frac{1}{25}$ ，大量重复做这种试验，平均每5000次事件A发生的次数是.

查看试题解析
14. 以 $40 m / s$ 的速度将小球沿与地面成 $30$ 度角的方向击出时，球的飞行路线是一条抛物线.如果不考虑空气阻力，球的飞行高度h（单位m）与飞行时间t（单位s）之间具有函数关系： $h = 20 t - 5 t^{2}$ ，那么球从飞出到落地要用的时间是.

查看试题解析
15. 如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝2.将△ABC绕点C旋转得到△EDC，使点D在AB边上，斜边DE交AC边于点F，则图中△CDF的周长为.

查看试题解析
16. 如图，四边形ABCD是矩形，AB=4，AD= $2 \sqrt{2}$ ，以点A为圆心，AB长为半径画弧，交CD于点E，交AD的延长线于点F，则图中阴影部分的面积是.

查看试题解析

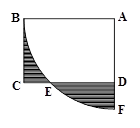
三、解答题

17. 关于x的一元二次方程（a﹣6）x²﹣8x+9＝0有实数根.

(1)、求a的最大整数值；

(2)、当a取最大整数值时，求出该方程两根.

查看试题解析
18. 某商品现在的售价为每件60元，每天可卖出300件.市场调查发现：如果调整价格，每降价1元，每天可多卖出20件.已知商品的进价为每件40元，如何定价既能使商品尽快卖出，又能使每天的利润达到6000元？

查看试题解析
19. 学生甲与学生乙学习概率初步知识后设计了如下游戏：学生甲手中有6，8，10三张扑克牌，学生乙手中有5，7，9三张扑克牌，每人从各自手中取一张牌进行比较，数字大的为本局获胜，每次获取的牌不能放回．

(1)、若每人随机取手中的一张牌进行比较，请列举出所有情况；

(2)、并求学生乙本局获胜的概率．

查看试题解析
20. 已知：过点A（3，0）直线l₁：y＝x+b与直线l₂：y＝﹣2x交于点B.抛物线y＝ax²+bx+c的顶点为B.

(1)、求点B的坐标；

(2)、如果抛物线y＝ax²+bx+c经过点A，求抛物线的表达式；

(3)、直线x＝﹣1分别与直线l₁ ， l₂交于C，D两点，当抛物线y＝ax²+bx+c与线段CD有交点时，求a的取值范围.

查看试题解析
21. 如图，将一个钝角△ABC（其中∠ABC＝120°）绕
点B顺时针旋转得△A₁BC₁ ，使得C点落在AB的延长线上的点C₁处，连结AA₁.

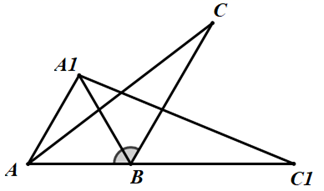(1)、写出旋转角的度数；

(2)、求证：∠A₁AC＝∠C₁.

查看试题解析
22. 如图，在Rt△ABC中，∠ACB＝90°，以AC为直径的⊙O与AB边交于点D，E为BC的中点，连接DE.

(1)、求证：DE是⊙O的切线；

(2)、若AC＝BC，判断四边形OCED的形状，并说明理由.

查看试题解析
23. 某商店购进一批成本为每件30元的商品.经调查发现，该商品每天的销售量y（件）与销售单价x（元）之间满足一次函数关系，其图象如图所示.

(1)、求该商品每天的销售量y与销售单价x之间的函数关系式；

(2)、若商店按单价不低于成本价且不高于50元销售，则销售单价定为多少，才能使销售该商品每天获得的利润最大？最大利润是多少？

(3)、若商店要使销售该商品每天获得的利润不低于800元，试利用函数图象确定销售单价最多为多少元？

查看试题解析
24.

（问题背景）如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，BE，点P为DC的中点.

(1)、（观察猜想）观察图1，猜想线段AP与BE的数量关系是，位置关系是.

(2)、（拓展探究）把△ADE绕点A逆时针方向旋转到图2的位置，（1）中的结论是否仍然成立，若成立，请证明：否则写出新的结论并说明理由.

(3)、（问题解决）把△ADE绕点A在平面内自由旋转，若DE＝4，BC＝8，请直接写出线段AP长的取值范围.

查看试题解析
25. 如图，已知抛物线y＝ax²+bx+c的图象与x轴交于点A，B（点A在点B的右侧），且与y轴交于点C，若OA＝OC，一元二次方程ax²+bx+c＝0的两根为1和3，点P是该抛物线上的一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD $//$ y轴，交AC于点D.

(1)、求该抛物线的函数关系式；

(2)、当△ADP是直角三角形时，求点P的坐标；

(3)、在题（2）的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A、P、E、F为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由.

查看试题解析