贵州威宁县2021届九年级上学期数学期末考试试卷(A卷)
试卷更新日期:2021-04-08 类型:期末考试
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 小明同学拿一个等边三角形木框在太阳光下观察其投影,此木框在水平地面上的影子不可能是( )A、
 B、
B、 C、
C、 D、
D、 3. 以下列长度(同一单位)为长的四条线段中,成比例的是( )A、1,2,3,4 B、2,10,15,5 C、2,4,8,16 D、2,12,12,44. 用一个10倍的放大镜去观察一个三角形,下列说法中正确的是( )
3. 以下列长度(同一单位)为长的四条线段中,成比例的是( )A、1,2,3,4 B、2,10,15,5 C、2,4,8,16 D、2,12,12,44. 用一个10倍的放大镜去观察一个三角形,下列说法中正确的是( )①三角形的每个角都扩大10倍;②三角形的每条边都扩大10倍;
③三角形的面积扩大10倍;④三角形的周长扩大10倍.
A、①② B、①③ C、②④ D、②③5. 某物体对地面的压力为定值,物体对地面的压强 与受力面积 之间的函数关系如图所示,这一函数表达式为( )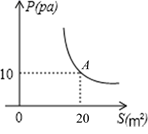 A、 B、 C、 D、6. 如图所示的“中”字,俯视图是( )
A、 B、 C、 D、6. 如图所示的“中”字,俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 在数学活动课上,老师让同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的有( )
7. 在数学活动课上,老师让同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的有( )①测量对角线是否相互平分;②测量两组对边是否相等;
③测量对角线是否相等;④测量其中三个角是否为直角
A、1个 B、2个 C、3个 D、4个8. 小颖在探索一元二次方程 的近似解时作了如下列表计算.观察表中对应的数据,可以估计方程的其中一个解的整数部分是( )x
0
1
2
3
5
A、0 B、1 C、2 D、39. 如图,一根木棍 斜靠在与地面 垂直的墙 上,设木棍中点为P,若木棍全端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离将( ) A、变化不定 B、变小 C、不变 D、变大10. 某校的校园内有一个由两个相同的正六边形(边长为 )围成的花坛,如图中的阴影部分所示,校方先要将这个花坛在原有的基础上扩建成一个如图所示区域,并在新扩充的部分种上草坪,则扩建后区域的周长为( )
A、变化不定 B、变小 C、不变 D、变大10. 某校的校园内有一个由两个相同的正六边形(边长为 )围成的花坛,如图中的阴影部分所示,校方先要将这个花坛在原有的基础上扩建成一个如图所示区域,并在新扩充的部分种上草坪,则扩建后区域的周长为( ) A、 B、 C、 D、11. 一种雨伞的截面图(如图所示),伞骨 ,支掌杆 ,当点O沿 滑动时,雨伞开闭.若 , ,此时B、D两点间的距离等于( )
A、 B、 C、 D、11. 一种雨伞的截面图(如图所示),伞骨 ,支掌杆 ,当点O沿 滑动时,雨伞开闭.若 , ,此时B、D两点间的距离等于( )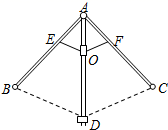 A、 B、 C、 D、12. 如图,扇子(阴影部分)的圆心角为x,余下扇形的圆心角为y,x与y的比通常按黄金比来设计,这样的扇子外形较美观.若黄金比为0.6,则x为( )
A、 B、 C、 D、12. 如图,扇子(阴影部分)的圆心角为x,余下扇形的圆心角为y,x与y的比通常按黄金比来设计,这样的扇子外形较美观.若黄金比为0.6,则x为( ) A、100 B、120 C、135 D、16013. 如图,将矩形纸片 沿其对角线 折叠,使点B落到点 的位置, 与 交于点E,若 , ,则图中阴影部分的周长为( )
A、100 B、120 C、135 D、16013. 如图,将矩形纸片 沿其对角线 折叠,使点B落到点 的位置, 与 交于点E,若 , ,则图中阴影部分的周长为( )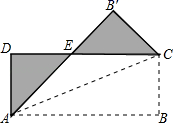 A、10 B、13 C、17 D、2014. 某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
A、10 B、13 C、17 D、2014. 某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( ) A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、掷一个质地均匀的正方体骰子,落地时面朝上的点数是6 C、一次掷两枚质地均匀的硬币,出现两枚硬币都正面朝上 D、用2,3,4三个数字随机排成一个三位数,排出的数是偶数15. 如图, 、 、…、 是双曲线 上的点,它们的横坐标分别为1、2、…2020, 、 、…、 分别垂直于x轴,垂足分别为 、 、…、 ,则 的面积为( )
A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、掷一个质地均匀的正方体骰子,落地时面朝上的点数是6 C、一次掷两枚质地均匀的硬币,出现两枚硬币都正面朝上 D、用2,3,4三个数字随机排成一个三位数,排出的数是偶数15. 如图, 、 、…、 是双曲线 上的点,它们的横坐标分别为1、2、…2020, 、 、…、 分别垂直于x轴,垂足分别为 、 、…、 ,则 的面积为( ) A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
16. 已知 ,则 的值为.17. 若关于x的一元二次方程 有两个相等实数根,则m的值是.18. 如图,点B,C分别是锐角 两边上的点, ,分别以点B,C为圆心,以 的长为半径画弧,两弧相交于点D,连接 , .则四边形 是.
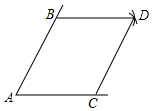 19. 对于任意的两个数a,b,定义一种运算※如下: ,如 .那么 .20. 如图,在正方形 中, ,点E在边 上, .将 沿 对折至 ,延长 交边 于点G,连接 , .有下列结论:① ;② ;③ ;④ .其中正确的结论是.(填序号)
19. 对于任意的两个数a,b,定义一种运算※如下: ,如 .那么 .20. 如图,在正方形 中, ,点E在边 上, .将 沿 对折至 ,延长 交边 于点G,连接 , .有下列结论:① ;② ;③ ;④ .其中正确的结论是.(填序号)
三、解答题
-
21. 解方程(1)、 (用配方法解)(2)、 (解法不限)22. 从 、 、1、2中取一个值作为横坐标a,再取一个作为纵坐标b,点 请用树状图列表的方法求M在双曲线 的图象上的概率.23. 阅读理解:
解方程时,我们经常将整体多次出现的部分打包进行换元处理,从而达到了降次、转整等目的,这一“神奇”的方法叫换元法.
例如:解方程
解:设
原方程化为:
∴
∴ 或 ∴ ,
当 时,即
∴ 或
,
当 时,即
∴ 或
∴ ,
∴原方程的解是: , , ,
请你利用换元法解方程:
24. 如图所示,身高1.5米的小明从路灯下的A点经过,测量得身后的影子 的长5米,沿 所在的直线行走10米到B点时,身后的影子 长为2米. (1)、请你确定路灯P的位置(2)、求路灯P距到地面的距离.25. 某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.(1)、当每个纪念品定价为3.5元时,商店每天能卖出件;(2)、如果商店要实现每天800元的销售利润,那该如何定价?
(1)、请你确定路灯P的位置(2)、求路灯P距到地面的距离.25. 某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.(1)、当每个纪念品定价为3.5元时,商店每天能卖出件;(2)、如果商店要实现每天800元的销售利润,那该如何定价?

