广西壮族自治区贺州市平桂区2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-08 类型:期末考试
一、单选题
-
1. sin45°的值是( ).A、 B、 C、1 D、2. 抛物线y=-(x-2)2+3的顶点坐标是( ).A、(-2,3) B、(2,3) C、(2,-3) D、(-2,-3)3. 已知线段a﹦4cm,线段b﹦7cm,则a﹕b的值是( ).A、1﹕4 B、1﹕7 C、4﹕7 D、7﹕44. 在4×4网格中,∠α的位置如图所示,则tanα的值为( )
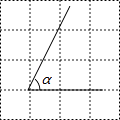 A、 B、 C、2 D、5. 某反比例函数的图象经过点(-1,6),则此函数图象也经过点 ( )A、 B、 C、 D、6. 在比例尺是1﹕10000的贺州市城区地图上,向阳路的长度约为10cm,它的实际长度约为( ).A、1000m B、1000cm C、100m D、100cm7. 已知反比例函数 (k为常数)的图象位于第一、三象限,则k的取值范围是( )A、 B、 C、 D、8. 已知△ABC∽△DEF,面积比为1﹕4,AC的对应边为DF, AC=2,则DF的长是( ).A、8 B、6 C、4 D、29. 在Rt△ABC中,∠C=90°, ,AC=8cm,则BC的长度为( ).A、3cm B、4cm C、5cm D、6cm10. 下列函数的值永远大于0的是 ( ) .A、 B、 C、 D、11. 如图,BE⊥AC于点B,CD⊥AC于点C,点A,E,D在同一条直线上,若BE=1.2,AB=1.6,BC=8.4,则CD的长是( ) .
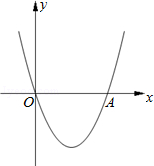
A、 B、 C、2 D、5. 某反比例函数的图象经过点(-1,6),则此函数图象也经过点 ( )A、 B、 C、 D、6. 在比例尺是1﹕10000的贺州市城区地图上,向阳路的长度约为10cm,它的实际长度约为( ).A、1000m B、1000cm C、100m D、100cm7. 已知反比例函数 (k为常数)的图象位于第一、三象限,则k的取值范围是( )A、 B、 C、 D、8. 已知△ABC∽△DEF,面积比为1﹕4,AC的对应边为DF, AC=2,则DF的长是( ).A、8 B、6 C、4 D、29. 在Rt△ABC中,∠C=90°, ,AC=8cm,则BC的长度为( ).A、3cm B、4cm C、5cm D、6cm10. 下列函数的值永远大于0的是 ( ) .A、 B、 C、 D、11. 如图,BE⊥AC于点B,CD⊥AC于点C,点A,E,D在同一条直线上,若BE=1.2,AB=1.6,BC=8.4,则CD的长是( ) . A、4.8 B、5 C、6 D、7.512. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac>0;④a-b+c>0;⑤3a+c<0.正确的个数是( ) .
A、4.8 B、5 C、6 D、7.512. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac>0;④a-b+c>0;⑤3a+c<0.正确的个数是( ) . A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
13. 若 ,则 .14. 已知:∠A+∠B=90°,若sinA= ,则cosB=.15. 抛物线y=x2向左平移1个单位,再向上平移5个单位所得函数解析式为.16. Rt△ABC中,∠C=90°,AC∶BC=1∶ ,则∠A=.17. 已知二次函数y=-x2+2x+1,若y随x增大而增大,则x的取值范围是.18. 如图,在△ABC中,∠B的平分线交AC于点D,DE//AB,若AB=9,BC=6, ,则 等于 .

三、解答题
-
19. 计算:20. 已知抛物线的顶点是(-2,3),且经过点(-1,4),求这条抛物线的函数表达式.21. 如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,请按要求完成下面的问题:
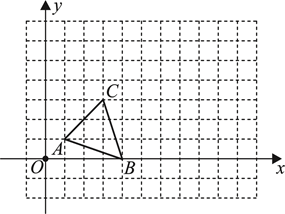 (1)、以图中的点O为位似中心,将△ABC同向作位似变换且放大到原来的两倍得到△A1B1C1 , 画出△A1B1C1;(2)、在(1)的条件下,若△ABC内有一点P的坐标为(3,2),求位似变化后对应的点P′的坐标.22. 如图,点A是反比例函数y=图象上的一点,过点A作AB⊥x轴于点B,连接OA,若△OAB的面积为2,求该反比例函数的解析式.
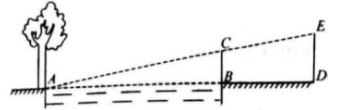
(1)、以图中的点O为位似中心,将△ABC同向作位似变换且放大到原来的两倍得到△A1B1C1 , 画出△A1B1C1;(2)、在(1)的条件下,若△ABC内有一点P的坐标为(3,2),求位似变化后对应的点P′的坐标.22. 如图,点A是反比例函数y=图象上的一点,过点A作AB⊥x轴于点B,连接OA,若△OAB的面积为2,求该反比例函数的解析式. 23. 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A , 在他们所在的岸边选择了点B , 使得AB与河岸垂直,并在B点竖起标杆BC , 再在AB的延长线上选择点D竖起标杆DE , 使得点E与点C、A共线.
23. 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A , 在他们所在的岸边选择了点B , 使得AB与河岸垂直,并在B点竖起标杆BC , 再在AB的延长线上选择点D竖起标杆DE , 使得点E与点C、A共线.已知:CB⊥AD , ED⊥AD , 测得BC=1m , DE=1.5m , BD=8.5m . 测量示意图如图所示.请根据相关测量信息,求河宽AB .
 24. 如图,一艘游轮从点A出发,与望海楼B的距离为90海里,在望海楼B 测得游轮A位于B处的南偏西30°方向,游轮沿正北方向行驶一段时间后到达C处,此时望海楼B海务接到消息,游轮A上携带有危险物品,必须马上出警拦截.这时在望海楼B测得C处位于B的南偏西60°的方向,游轮正以每小时20海里的速度沿正北方向行驶,求望海楼B处的海务船至少要以怎样的速度最近距离拦截下游轮A?( 取1.73,结果保留整数).
24. 如图,一艘游轮从点A出发,与望海楼B的距离为90海里,在望海楼B 测得游轮A位于B处的南偏西30°方向,游轮沿正北方向行驶一段时间后到达C处,此时望海楼B海务接到消息,游轮A上携带有危险物品,必须马上出警拦截.这时在望海楼B测得C处位于B的南偏西60°的方向,游轮正以每小时20海里的速度沿正北方向行驶,求望海楼B处的海务船至少要以怎样的速度最近距离拦截下游轮A?( 取1.73,结果保留整数).