甘肃省张掖市山丹县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-08 类型:期末考试
一、单选题
-
1. 在Rt△ABC中,若∠C=90°,AC=4,AB=5,则tanB=( )A、 B、 C、 D、2. 一元二次方程x2﹣x﹣3=0的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. 对于反比例函数 ,下列说法不正确的是A、图象分布在第二、四象限 B、当 时, 随 的增大而增大 C、图象经过点(1,-2) D、若点 , 都在图象上,且 ,则4. 如图,DE是△ABC的中位线,已知△ABC的面积为8 ,则△ADE的面积为( ) .
 A、2 B、4 C、6 D、85. 如图所示几何体的左视图正确的是( )
A、2 B、4 C、6 D、85. 如图所示几何体的左视图正确的是( )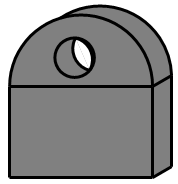 A、
A、 B、
B、 C、
C、 D、
D、 6.
6.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 . 若设道路的宽为xm,则下面所列方程正确的是( )
 A、(32﹣2x)(20﹣x)=570 B、32x+2×20x=32×20﹣570 C、(32﹣x)(20﹣x)=32×20﹣570 D、32x+2×20x﹣2x2=5707. 在同一平面直角坐标系中,函数y=x﹣1与函数 的图象可能是A、
A、(32﹣2x)(20﹣x)=570 B、32x+2×20x=32×20﹣570 C、(32﹣x)(20﹣x)=32×20﹣570 D、32x+2×20x﹣2x2=5707. 在同一平面直角坐标系中,函数y=x﹣1与函数 的图象可能是A、 B、
B、 C、
C、 D、
D、 8. 如图,将△ABC放在每个小正方形的边长都为1的网格中,点A,B,C均在格点上,则tanA的值是( )
8. 如图,将△ABC放在每个小正方形的边长都为1的网格中,点A,B,C均在格点上,则tanA的值是( )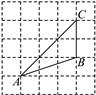 A、 B、 C、2 D、9. 下列说法中,正确的说法有( )
A、 B、 C、2 D、9. 下列说法中,正确的说法有( )①对角线互相平分且相等的四边形是菱形;
②一元二次方程 的根是 , ;
③两个相似三角形的周长的比为 ,则它们的面积的比为 ;
④对角线互相垂直的平行四边形为正方形;
⑤对角线垂直的四边形各边中点得到的四边形是矩形.
A、1个 B、2个 C、3个 D、4个10. 如图,点A、B是双曲线 上的点,分别经过A、B两点向x轴、y轴作垂线段,若 则 ( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 若 = ,则 = .12. 已知线段AB=2,点C为AB的黄金分割点,且AC<BC , 那么BC= .13. 某公司2016年的产值为500万元,2018年的产值为720万元,则该公司产值的年平均增长率为.14. 如图,点A是双曲线 上的任意一点,过点A作AB⊥x轴于B,若△OAB的面积为8,则k=.
 15. 如图,用两个可自由转动的转盘做“配紫色”游戏:分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配出紫色,那么可配成紫色的概率是.
15. 如图,用两个可自由转动的转盘做“配紫色”游戏:分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配出紫色,那么可配成紫色的概率是. 16. 若关于 的方程 有两个相等的实数根,则 的值是.17. 如图所示,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为24,则OH的长等于 .
16. 若关于 的方程 有两个相等的实数根,则 的值是.17. 如图所示,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为24,则OH的长等于 . 18. 如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y= (k>0,x>0)的图象经过AC的中点D,则k的值为 .
18. 如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y= (k>0,x>0)的图象经过AC的中点D,则k的值为 .
三、解答题
-
19.(1)、(2)、 (配方法)(3)、(4)、4x(x﹣2)=x﹣220. 如图,已知D、E分别是△ABC的边AC、AB上的点,若∠A=35°,∠C=85°,∠ADE=60°.
 (1)、请说明:△ADE∽△ABC;(2)、若AD=4,AE=3,BE=5,求AC的长.21. 若反比例函数y= 与一次函数y=mx﹣4的图象都经过点A(a,2).
(1)、请说明:△ADE∽△ABC;(2)、若AD=4,AE=3,BE=5,求AC的长.21. 若反比例函数y= 与一次函数y=mx﹣4的图象都经过点A(a,2). (1)、求点A的坐标;(2)、求一次函数y=mx﹣4的解析式;(3)、设O为坐标原点,若两个函数图象的另一个交点为B,求△AOB的面积.22. 如图,已知E、F为平行四边形ABCD的对角线上的两点,且BE=DF,∠AEC=90°.求证:四边形AECF为矩形.
(1)、求点A的坐标;(2)、求一次函数y=mx﹣4的解析式;(3)、设O为坐标原点,若两个函数图象的另一个交点为B,求△AOB的面积.22. 如图,已知E、F为平行四边形ABCD的对角线上的两点,且BE=DF,∠AEC=90°.求证:四边形AECF为矩形. 23. 如图,线段AB、DC分别表示甲、乙两建筑物的高,
23. 如图,线段AB、DC分别表示甲、乙两建筑物的高, ,
,
 ,从B点测得D点的仰角 为60°,从A点测得D点
,从B点测得D点的仰角 为60°,从A点测得D点的仰角 为30°,已知甲建筑物高AB=36米.

(Ⅰ)求乙建筑物的高DC;
(Ⅱ)求甲、乙两建筑物之间的距离BC(结果精确到0.01米).(参考数据: )
24. 如图,甲转盘被分成3个面积相等的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界上时,重转一次,直到指针指向一个区域为止).
 (1)、请你用画树状图或列表格的方法,求出点(x,y)落在第二象限内的概率;(2)、求出点(x,y)落在函数y=-
(1)、请你用画树状图或列表格的方法,求出点(x,y)落在第二象限内的概率;(2)、求出点(x,y)落在函数y=- 图象上的概率. 25. 淇淇和嘉嘉在习了利用相似三角形测高之后分别测量两个旗杆高度.(1)、如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E , 测得脚掌中心位置B到镜面中心C的距离是50cm , 镜面中心C距离旗杆底部D的距离为4m , 已知淇淇同的身高是1.54m , 眼睛位置A距离淇淇头顶的距离是4cm , 求旗杆DE 的高度.
图象上的概率. 25. 淇淇和嘉嘉在习了利用相似三角形测高之后分别测量两个旗杆高度.(1)、如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E , 测得脚掌中心位置B到镜面中心C的距离是50cm , 镜面中心C距离旗杆底部D的距离为4m , 已知淇淇同的身高是1.54m , 眼睛位置A距离淇淇头顶的距离是4cm , 求旗杆DE 的高度. (2)、如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为 米,∠DCE=45°,求旗杆AB的高度?
(2)、如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为 米,∠DCE=45°,求旗杆AB的高度? 26. 商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.(1)、若某天该商品每件降价3元,当天可获利多少元?(2)、设每件商品降价x元,则商场日销售量增加件,每件商品,盈利元(用含x的代数式表示);(3)、在上述销售正常情况下,每件商品降价多少元时,商场日盈利可达到2000元?27. 为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:
26. 商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.(1)、若某天该商品每件降价3元,当天可获利多少元?(2)、设每件商品降价x元,则商场日销售量增加件,每件商品,盈利元(用含x的代数式表示);(3)、在上述销售正常情况下,每件商品降价多少元时,商场日盈利可达到2000元?27. 为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题: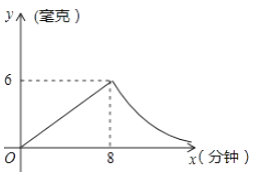 (1)、药物燃烧时,y关于x的函数关系式为 , 自变量x的取值范为;药物燃烧后,y关于x的函数关系式为 .(2)、研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过分钟后,员工才能回到办公室;(3)、研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?28. 直线y=kx+b与反比例函数 (x>0)的图象分别交于点A(m,4)和点B(8,n),与坐标轴分别交于点C和点D.
(1)、药物燃烧时,y关于x的函数关系式为 , 自变量x的取值范为;药物燃烧后,y关于x的函数关系式为 .(2)、研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过分钟后,员工才能回到办公室;(3)、研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?28. 直线y=kx+b与反比例函数 (x>0)的图象分别交于点A(m,4)和点B(8,n),与坐标轴分别交于点C和点D. (1)、求直线AB的解析式;(2)、观察图象,当x>0时,直接写出 的解集;(3)、若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
(1)、求直线AB的解析式;(2)、观察图象,当x>0时,直接写出 的解集;(3)、若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.