福建省漳州市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-08 类型:期末考试
一、单选题
-
1. 若 ,则 的值为( )A、 B、 C、 D、22. 下列图形是中心对称图形,但不是轴对称图形的是( )A、平行四边形 B、正方形 C、矩形 D、菱形3. 一元二次方程 配方后可变形为( )A、 B、 C、 D、4. 若反比例函数 的图像在第一、第三象限,则 可能取的一个值为( )A、0 B、1 C、2 D、35. 如图,在5×4的正方形网格中,每个小正方形的边长都是l,△ABC的顶点都在这些小正方形的顶点上,则cos∠BAC的值为( )
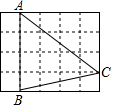 A、 B、 C、 D、6. 若点 都在反比例函数 图象上,则 的大小关系为( )A、 B、 C、 D、7. 如图,某商店营业大厅自动扶梯 的坡度为 ,过点B作 ,垂足为点C.若大厅水平距离 的长为 ,则两层之间的高度 为( )
A、 B、 C、 D、6. 若点 都在反比例函数 图象上,则 的大小关系为( )A、 B、 C、 D、7. 如图,某商店营业大厅自动扶梯 的坡度为 ,过点B作 ,垂足为点C.若大厅水平距离 的长为 ,则两层之间的高度 为( )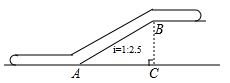 A、 B、 C、 D、8. 如图,以点O为位似中心,把 放大2倍得到 ,则以下说法中错误的是( )
A、 B、 C、 D、8. 如图,以点O为位似中心,把 放大2倍得到 ,则以下说法中错误的是( ) A、 B、 C、 D、点 三点在同一直线上9. 已知y是x的二次函数,y与x的部分对应值如表所示,若该二次函数图象向左平移后通过原点,则应平移( )
A、 B、 C、 D、点 三点在同一直线上9. 已知y是x的二次函数,y与x的部分对应值如表所示,若该二次函数图象向左平移后通过原点,则应平移( )x
…
-1
0
1
2
…
y
…
0
3
4
3
…
A、1个单位 B、2个单位 C、3个单位 D、4个单位10. 如图,在平面直角坐标系中,矩形 的对角线 轴,若 ,则点C的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若sinA= ,则锐角∠A=°.12. 若正方形 的对角线 的长为4,则该正方形的面积为.13. 如图,在 中, 分别为 边上的中点,则 与 的周长的比值是.
 14. 若关于x的方程 有一个根是3,则 的值是.15. 从 这四个数中任取两数,积为6的概率是.16. 如图,点A在双曲线 上,连接 ,作 ,交双曲线 于点B,若 ,则k的值为.
14. 若关于x的方程 有一个根是3,则 的值是.15. 从 这四个数中任取两数,积为6的概率是.16. 如图,点A在双曲线 上,连接 ,作 ,交双曲线 于点B,若 ,则k的值为.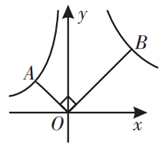
三、解答题
-
17. 解方程: .18. 如图,在 中,过点B作 ,垂足为E,过点C作 ,交 的延长线于点 .求证:四边形 是菱形.
 19. 我国古代数学著作《九章算术》中有“井深几何”问题:“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深儿何?”它的大意是:如图,已知四边形 是矩形, 尺, 尺, 尺,求井深 为多少尺?
19. 我国古代数学著作《九章算术》中有“井深几何”问题:“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深儿何?”它的大意是:如图,已知四边形 是矩形, 尺, 尺, 尺,求井深 为多少尺? 20. 如图,在 中, .
20. 如图,在 中, . (1)、求作点D,使四边形 是矩形;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,连接 ,若 ,求 的长.21. 新冠疫情期间,某校有“录播”和“直播”两种教学方式供学生自主选择其中一种进行居家线上学习.为了了解该校学生线上学习参与度情况,从选择这两种教学方式的学生中,分别随机抽取50名进行调查,调查结果如表(数据分组包含左端值不包含右端值).
(1)、求作点D,使四边形 是矩形;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,连接 ,若 ,求 的长.21. 新冠疫情期间,某校有“录播”和“直播”两种教学方式供学生自主选择其中一种进行居家线上学习.为了了解该校学生线上学习参与度情况,从选择这两种教学方式的学生中,分别随机抽取50名进行调查,调查结果如表(数据分组包含左端值不包含右端值).
录播
5
18
14
13
直播
2
15
21
12
(1)、从选择教学方式为“录播”的学生中任意抽取1名学生,试估计该生的参与度不低于 的概率;(2)、若该校共有1200名学生,选择“录播”和“直播”的人数之比为 ,试估计选择“录播”或“直播”参与度均在 以下的共有多少人?22. 阅读下面材料,并完成问题.任意给定一个矩形A,若存在另一个矩形B,使它的周长和面积分别是矩形A的一半,则称矩形 是“兄弟矩形”.
探究:当矩形A的边长分别为7和1时,是否存在A的“兄弟矩形”B?
小亮同学是这样探究的:
设所求矩形的两边分别是x和y,由题意,得
由①,得 ,③
把③代入②,得 ,
整理,得 .
,
的“兄弟矩形”B存在.
(1)、若已知矩形A的边长分别为3和2,请你根据小亮的探究方法,说明A的“兄弟矩形”B是否存在?(2)、若矩形A的边长为m和n,当A的“兄弟矩形”B存在时,求 应满足的条件.23. 平安路上,多“盔”有你.在“交通安全宣传月”期间,某商店销售一批头盔,进价为每顶40元,售价为每顶68元,平均每周可售出100顶.商店计划将头盔降价销售,每顶售价不高于58元,经调查发现:每降价1元,平均每周可多售出20顶.(1)、若该商店希望平均每周获利4000元,则每顶头盔应降价多少?(2)、商店降价销售后,决定每销售1顶头盔,就向某慈善机构捐赠m元(m为整数,且 ),帮助做“交通安全”宣传.捐赠后发现,该商店每周销售这种商品的利润仍随售价的增大而增大,求m的值.