重庆市梁平区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-04-08 类型:期末考试
一、单选题
-
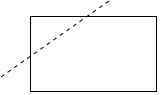
1. 中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么﹣80元表示( )A、支出20元 B、收入20元 C、支出80元 D、收入80元2. “比 的3倍大5的数”用代数式表示为( )A、 B、 C、 D、3. 下列式子化简不正确的是( )A、 B、 C、 D、4. 如图,用剪刀沿直线将一片平整的长方形纸片剪掉一部分,发现剩下纸片的周长比原纸片的周长要小,能正确解释这一现象的数学知识是
 A、经过两点,有且仅有一条直线 B、经过一点有无数条直线 C、两点之间,线段最短 D、垂线段最短5. 下列说法正确的是( )A、最小的整数是0 B、有理数分为正数和负数 C、如果两个数的绝对值相等,那么这两个数相等. D、互为相反数的两个数的绝对值相等6. 解方程 ,去分母,得( )A、 B、 C、 D、7. 已知:如图,∠AOB=90°,直线CD经过点O,∠AOC=130°,则∠BOD=( )
A、经过两点,有且仅有一条直线 B、经过一点有无数条直线 C、两点之间,线段最短 D、垂线段最短5. 下列说法正确的是( )A、最小的整数是0 B、有理数分为正数和负数 C、如果两个数的绝对值相等,那么这两个数相等. D、互为相反数的两个数的绝对值相等6. 解方程 ,去分母,得( )A、 B、 C、 D、7. 已知:如图,∠AOB=90°,直线CD经过点O,∠AOC=130°,则∠BOD=( )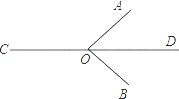 A、30° B、35° C、40° D、50°8. 如图,从边长为 的正方形纸片中剪去一个边长为 的正方形 ,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的周长为( )
A、30° B、35° C、40° D、50°8. 如图,从边长为 的正方形纸片中剪去一个边长为 的正方形 ,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的周长为( ) A、 B、 C、 D、9. 如图,点 把线段 分成两部分,其比为 ,点 是 的中点, ,则 的长为( )
A、 B、 C、 D、9. 如图,点 把线段 分成两部分,其比为 ,点 是 的中点, ,则 的长为( )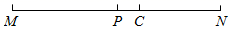 A、 B、 C、 D、10. 《九章算术》中有“盈不足术”的问题,原文如下:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数,羊价各幾何?”题意是:若干人共同出资买羊,每人出 元,则差 元;每人出 元,则差 元求人数和羊价各是多少?设买羊人数为x人,则根据题意可列方程为( )A、 B、 C、 D、11. 小明在某月的日历上圈出了三个数a、b、c,并求出了它们的和为39,则这三个数在日历中的排位位置不可能的是( )A、
A、 B、 C、 D、10. 《九章算术》中有“盈不足术”的问题,原文如下:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数,羊价各幾何?”题意是:若干人共同出资买羊,每人出 元,则差 元;每人出 元,则差 元求人数和羊价各是多少?设买羊人数为x人,则根据题意可列方程为( )A、 B、 C、 D、11. 小明在某月的日历上圈出了三个数a、b、c,并求出了它们的和为39,则这三个数在日历中的排位位置不可能的是( )A、 B、
B、 C、
C、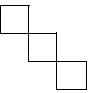 D、
D、 12. 在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码.有一种密码,将英文26个字母 , , , , (不论大小写)依次对应1,2,3, ,26这26个自然数(见表格),当明码对应的序号 为奇数时,密码对应的序号 ,当明码对应的序号 为偶数时,密码对应的序号 ,按下述规定,将明码“ ”译成密码是:
12. 在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码.有一种密码,将英文26个字母 , , , , (不论大小写)依次对应1,2,3, ,26这26个自然数(见表格),当明码对应的序号 为奇数时,密码对应的序号 ,当明码对应的序号 为偶数时,密码对应的序号 ,按下述规定,将明码“ ”译成密码是:字母
序号
1
2
3
4
5
6
7
8
9
10
11
12
13
字母
序号
14
15
16
17
18
19
20
21
22
23
24
25
26
A、 B、 C、 D、二、填空题
-
13. 单项式 的系数是 , 次数是.14. 某公交车原坐有22人,经过4个站点时,上下车情况记录如下(上车为正,下车为负):+4,-8,-5,+6,-3,+2,+1,-7.则车上还有 人.15. 港珠澳大桥世界闻名,连接香港大屿山、澳门半岛和广东省珠海市,总长约5500000米,2018年10月24日上午9时正式通车,用科学记数法表示5500000米应为米.16. 多项式 中,不含 项,则k的值为 .17. 无限循环小数如何化成分数呢?设x=0.333 ①, 则10x=3.333 ②, 则②-①,得9x=3,即x= , 所以0. =0.33 ,根据上述提供的方法:把 化成分数为.18. 对于一个运算 ,已知 ,那么 .
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 解一元一次方程:(1)、 ;(2)、 .21. 如图,射线 分别表示从点 出发北、东、南、西四个方向,将直角三角尺的直角顶点与点 重合.
 (1)、图中与 互余的角是或;(2)、①用直尺和量角器作 的平分线 ;
(1)、图中与 互余的角是或;(2)、①用直尺和量角器作 的平分线 ;②在①所做的图形中,如果 ,那么点 在点 北偏东 °的方向上(请说明理由).
22. 先化简,再求值:(1)、当 时,求 的值;(2)、 ,其中 .23. 小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东跑回到自己家.(1)、以小明家为原点,向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;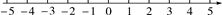 (2)、求小彬家与学校之间的距离;(3)、如果小明跑步的速度是250米/分钟,那么小明跑步一共用了多长时间?24. 某社区超市第一次总共用6000元购进甲、乙两种商品,其中甲商品的件数比乙商品件数的2倍少30件,甲、乙两种商品的进价如表:
(2)、求小彬家与学校之间的距离;(3)、如果小明跑步的速度是250米/分钟,那么小明跑步一共用了多长时间?24. 某社区超市第一次总共用6000元购进甲、乙两种商品,其中甲商品的件数比乙商品件数的2倍少30件,甲、乙两种商品的进价如表:甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)、求该超市第一次购进乙种商品的件数?(2)、甲乙两种商品的售价如上表,若将第一次所购商品全部卖完后,一共可获得多少利润?(3)、该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原售价销售,乙商品在原售价上打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多720元,求第二次乙种商品是按原价打几折销售?25. 一般情况下 不成立,但有些数可以使得它成立,例如: .我们称使得 成立的一对数 为“相伴数对”,记为 .(1)、填空: “相伴数对”(填是或否);(2)、若 是“相伴数对”,求 的值;(3)、若 是“相伴数对”,求代数式 的值.26. 在长方形 中,边 长度比 长度短10个单位长度,且 的长度是 长度的 .(1)、求 边的长;(2)、现有一动点 从 点出发,以每秒2个单位长度的速度沿折线路径 向终点 运动,在 点运动过程中,设运动时间为 秒,三角形 的面积为 ,试用含 的式子表示 ;(3)、在(2)的条件下,点 为 的中点,点 为 的中点,在点 出发的同时,动点 从点 出发,以4个单位/秒的速度沿 边匀速向左运动,当点 遇到点 后,立即按原速原路返回(调头时间忽略不计),且 回到点 时, 两点立即停止运动.当 时,请求出满足条件的 值?