江苏省盐城市射阳县2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-04-08 类型:期末考试
一、单选题
-
1. 如图,下列生活物品中,从整体上看,形状是圆柱的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知 ,0, , , , 中单项式有( )A、3个 B、4个 C、5个 D、6个3. 据美国媒体报道,截止2020年12月13日,美国累计新冠肺炎确诊病例达到1670万,其中确诊病例达到第一个800万例用时268天,第二个800万例仅用了57天.目前美国平均每小时有近100名美国人死于新冠肺炎,新冠肺炎疫情持续恶化.将数字1670万用科学记数法表示应为( )A、 B、 C、 D、4. 如图是一个正方体展开图,把展开图折叠成正方体后,“抗”字一面相对面上的字是( )
2. 已知 ,0, , , , 中单项式有( )A、3个 B、4个 C、5个 D、6个3. 据美国媒体报道,截止2020年12月13日,美国累计新冠肺炎确诊病例达到1670万,其中确诊病例达到第一个800万例用时268天,第二个800万例仅用了57天.目前美国平均每小时有近100名美国人死于新冠肺炎,新冠肺炎疫情持续恶化.将数字1670万用科学记数法表示应为( )A、 B、 C、 D、4. 如图是一个正方体展开图,把展开图折叠成正方体后,“抗”字一面相对面上的字是( )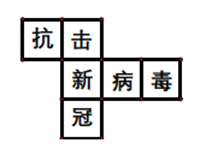 A、新 B、冠 C、病 D、毒5. 如图,直线AB和CD相交于O,那么图中 ∠DOE与∠COA 的关系是( )
A、新 B、冠 C、病 D、毒5. 如图,直线AB和CD相交于O,那么图中 ∠DOE与∠COA 的关系是( )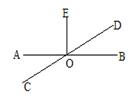 A、对顶角 B、相等 C、互余 D、互补6. 下列等式变形正确的是( )A、如果a=b,那么a+3=b-3 B、如果3a-7=5a,那么3a+5a=7 C、如果3x=-3,那么6x=-6 D、如果2x=3,那么x=7. 如图,下列说法中错误的是( ).
A、对顶角 B、相等 C、互余 D、互补6. 下列等式变形正确的是( )A、如果a=b,那么a+3=b-3 B、如果3a-7=5a,那么3a+5a=7 C、如果3x=-3,那么6x=-6 D、如果2x=3,那么x=7. 如图,下列说法中错误的是( ).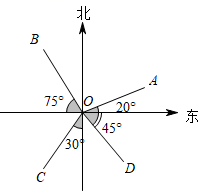 A、 方向是北偏东20° B、 方向是北偏西15° C、 方向是南偏西30° D、 方向是东南方向8. 如图是边长为 的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是( )
A、 方向是北偏东20° B、 方向是北偏西15° C、 方向是南偏西30° D、 方向是东南方向8. 如图是边长为 的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是( )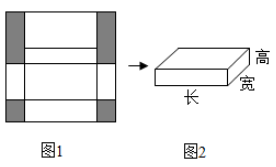 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 单项式-2x2y的系数是 , 次数是.10. 如图,已知 , ,所以点 三点共线的理由.
 11. 如果 是关于 的方程 的解,那么 的值是.12. .13. 化简: .14. 一个角的补角加上 后,等于这个角的余角的4倍,则这个角等于 .15. 如图,已知 , 、 分别是 、 的中点,且 ,则 的长度为 .
11. 如果 是关于 的方程 的解,那么 的值是.12. .13. 化简: .14. 一个角的补角加上 后,等于这个角的余角的4倍,则这个角等于 .15. 如图,已知 , 、 分别是 、 的中点,且 ,则 的长度为 .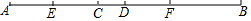
三、解答题
-
16. 计算:(1)、(2)、17. 解方程:(1)、(2)、18. 先化简,再求值:已知 , ,求 的值.19. 在平整的地面上,有若干个完全相同棱长为1的小正方体堆成一个几何图所示.

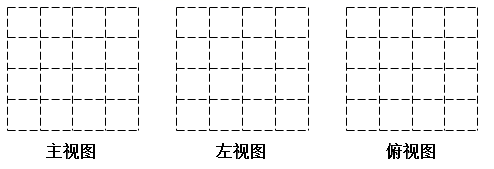 (1)、请画出这个几何体的三视图.(2)、若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加个小正方体.(3)、如果需要给原来这个几何体表面喷上红漆,则喷漆面积是多少?20. 如图,所有小正方形的边长都为1,O、A、B、C都在格点上.
(1)、请画出这个几何体的三视图.(2)、若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加个小正方体.(3)、如果需要给原来这个几何体表面喷上红漆,则喷漆面积是多少?20. 如图,所有小正方形的边长都为1,O、A、B、C都在格点上.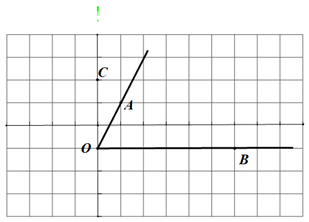 (1)、过点C画直线OA、OB的平行线分别交直线OB、OA于点D、点E(不写画法,下同);
(1)、过点C画直线OA、OB的平行线分别交直线OB、OA于点D、点E(不写画法,下同);
过点A画直线OB的垂线,并注明垂足为F;过点A画直线OA的垂线,交射线OB于点G.(2)、线段的长度是点A到直线OB的距离;(3)、通过度量,你发现 分别与 、 怎样的关系?21. 2020年11月份,某人民商场开展了“内购专场·浓情答谢”闭门销售活动,本次活动中的服装消费券单笔交易满900元立减168元(每次只能使用一张).某品牌服装按进价提高50%后标价,若按标价的八折销售,某顾客购买该品牌服装时使用一张服装消费券后,又付现金768元.求该品牌服装的进价.22. 如图, 为线段 上一点, 为 的中点, , .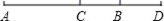 (1)、图中共有条线段;(2)、求 的长;(3)、若点 在线段 上,且 ,求 的长.23. 如图所示,直线 , 交于点 , 平分 , 于点 , ,求 和 的度数.
(1)、图中共有条线段;(2)、求 的长;(3)、若点 在线段 上,且 ,求 的长.23. 如图所示,直线 , 交于点 , 平分 , 于点 , ,求 和 的度数.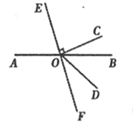 24. (新知理解)
24. (新知理解)如图①,点 在线段 上,图中共有三条线段 、 和 ,若其中有一条线段的长度是另外一条线段长度的2倍,则称点 是线段 的“奇点”.
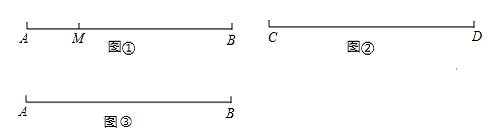 (1)、线段的中点这条线段的“奇点”(填“是”或“不是”)(2)、(初步应用)
(1)、线段的中点这条线段的“奇点”(填“是”或“不是”)(2)、(初步应用)如图②,若 ,点 是线段 的奇点,则 CNcm;
(3)、(解决问题)如图③,已知 动点 从点 出发,以 速度沿 向点 匀速移动:点 从点 出发,以 的速度沿 向点 匀速移动,点 、 同时出发,当其中一点到达终点时,运动停止,设移动的时间为 ,请直接写出 为何值时, 、 、 三点中其中一点恰好是另外两点为端点的线段的奇点?