江苏省淮安市淮安区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-04-08 类型:期末考试
一、单选题
-
1. 如果温度上升 ,记作 ,那么温度下降 记作( )A、 B、 C、 D、2. 计算 ,结果正确的是 ( )A、-4 B、-3 C、-2 D、-13. 将 42000这个数用科学记数法表示正确的是( )A、42×103 B、4.2×104 C、0.42×105 D、4.2×1034. 单项式-8ab的系数是( )A、8 B、-8 C、8a D、-8a5. 已知 2xn+1y3与 x4y3是同类项,则n的值是( )A、5 B、4 C、3 D、26. 若多项式2x2+3x+7的值为10.则多项式6x2+9x-8的值为( )A、1 B、2 C、3 D、47. 下列立体图形含有曲面的是( )A、
 B、
B、 C、
C、 D、
D、 8. 在下图中,∠1和∠2是对顶角的是( )A、
8. 在下图中,∠1和∠2是对顶角的是( )A、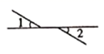 B、
B、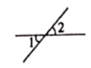 C、
C、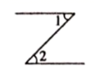 D、
D、
二、填空题
-
9. 今年冬天某天温度最高是-3℃,最低是-12℃,这一天温差是℃.10. 在数轴上,表示-2 的点与原点的距离是个单位长度.11. 去括号: .12. 已知x=1是方程x+2m=7的解,则m= .13. 某正方体的每个面上都有一个汉字,如图是它的一个展开图,则在原正方体中,与“我”字所在面相对的面上的汉字是.
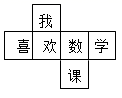 14. 已知C是线段AB中点,若 AB=5cm,则BC=.15. 如图,点A,B,C在直线l上,PB⊥l , PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是cm.
14. 已知C是线段AB中点,若 AB=5cm,则BC=.15. 如图,点A,B,C在直线l上,PB⊥l , PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是cm.
 16. 一件衣服售价为 200元,现六折销售,仍可获利20%,则这件衣服的进价是元.
16. 一件衣服售价为 200元,现六折销售,仍可获利20%,则这件衣服的进价是元.三、解答题
-
17. 计算:(1)、(-2)3+ ×8.(2)、18. 解方程:(1)、4x-3=2(x-1)(2)、x- = 1+19. 先化简,再求值:(3a2-ab+7)-(5ab-4a2+7),其中a=2,b= .20. “绿水青山就是金山银山”,某省2018年新建湿地公园和森林公园共42个,其中森林公园比湿地公园多4个.问该省2018年新建湿地公园和森林公园各多少个?21. 如图,是由几个大小完全相同的小正方体垒成的几何体.
 (1)、请分别画出你所看到的几何体的三视图;(2)、图中共有个小正方体.22. 如图,△ABC的三个顶点均在格点处.
(1)、请分别画出你所看到的几何体的三视图;(2)、图中共有个小正方体.22. 如图,△ABC的三个顶点均在格点处.
( 1 )过点B画AC 的平行线 BD;
( 2 )过点A画 BC 的垂线AE;(请用黑水笔描清楚)
23. 一个角的余角比它的补角的 还少15°,求这个角的度数.24. 如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=20°,求∠COD的度数. 25. 已知数轴上的点A和点B之间的距离为28个单位长度,点A在原点左边,距离原点 8 个单位长度,点B在原点的右边.(1)、请直接写出 A、B 两点所对应的数.(2)、数轴上点A以每秒1个单位长度的速度出发向左运动,同时点B以每秒3个单位长度的速度出发向左运动,经过t秒后点B在点C处追上了点A.请求出t的值并求出 C 点对应的数.26. 若A、O、B三点共线,∠BOC=50°,将一个三角板的直角顶点放在点O处(注:∠DOE=90°,∠DEO=30°).
25. 已知数轴上的点A和点B之间的距离为28个单位长度,点A在原点左边,距离原点 8 个单位长度,点B在原点的右边.(1)、请直接写出 A、B 两点所对应的数.(2)、数轴上点A以每秒1个单位长度的速度出发向左运动,同时点B以每秒3个单位长度的速度出发向左运动,经过t秒后点B在点C处追上了点A.请求出t的值并求出 C 点对应的数.26. 若A、O、B三点共线,∠BOC=50°,将一个三角板的直角顶点放在点O处(注:∠DOE=90°,∠DEO=30°). (1)、如图1,使三角板的短直角边OD在射线OB上,则∠COE=°;(2)、如图2,将三角板 DOE 绕点O逆时针方向旋转,若OE恰好平分∠AOC,则OD所在射线是∠BOC 的;(3)、如图3,将三角板 DOE绕点O逆时针转动到使∠COD= ∠AOE时,求∠BOD的度数;(4)、将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t 秒时,OE恰好与直线OC 重合,求t的值.
(1)、如图1,使三角板的短直角边OD在射线OB上,则∠COE=°;(2)、如图2,将三角板 DOE 绕点O逆时针方向旋转,若OE恰好平分∠AOC,则OD所在射线是∠BOC 的;(3)、如图3,将三角板 DOE绕点O逆时针转动到使∠COD= ∠AOE时,求∠BOD的度数;(4)、将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t 秒时,OE恰好与直线OC 重合,求t的值.