湖北省武汉市三校联合体2019-2020学年高二下学期数学期中考试试卷

试卷更新日期：2021-04-08 类型：期中考试

进入出卷网下载

一、单选题

1. 袋中有3个白球、5个黑球，从中任取2个，可以作为离散型随机变量的是（）

A、至少取到1个白球 B、至多取到1个白球 C、取到白球的个数 D、取到的球的个数

查看试题解析
2. ${(x - 1)}^{10}$ 的展开式的第6项的系数是（）

A、 $- C_{10}^{6}$ B、 $C_{10}^{6}$ C、 $- C_{10}^{5}$ D、 $C_{10}^{5}$

查看试题解析
3. 记 $ξ ， η$ 为两个离散型随机变量，则下列结论不正确的是（）

A、 $E (2 ξ + 1) = 2 E ξ + 1$ B、 $D (η - 2) = D η$ C、 $E (ξ + η) = E ξ + E η$ D、 $D (ξ + η) = D ξ + D η$

查看试题解析
4. 已知变量 $x$ ， $y$ 之间的线性回归方程为 $\hat{y} = - 0.7 x + 10.3$ ，且变量 $x$ ， $y$ 之间的一组相关数据如表所示，则下列说法错误的是（）

$x$

6

8

10

12

$y$

6

$m$

3

2

A、变量 $x$ ， $y$ 之间呈负相关关系 B、 $m = 4$ C、可以预测，当 $x = 20$ 时， $\hat{y} = - 3.7$ D、该回归直线必过点 $(9, 4)$

查看试题解析
5. 如图是调查某地区男女中学生喜欢理科的等高条形图，阴影部分表示喜欢理科的百分比，从图中可以看出（）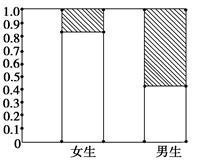

A、性别与喜欢理科无关 B、女生中喜欢理科的比为80% C、男生比女生喜欢理科的可能性大一些 D、男生不喜欢理科的比为60%

查看试题解析
6. 我国古代典籍《周易》用“卦”描述万物的变化．每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“——”和阴爻“— —”，如图就是一重卦．在所有重卦中随机取一重卦，则该重卦恰有3个阳爻的概率是（）

A、 $\frac{5}{16}$ B、 $\frac{11}{32}$ C、 $\frac{21}{32}$ D、 $\frac{11}{16}$

查看试题解析
7. 某校将5名插班生甲、乙、丙、丁、戊编入3个班级，每班至少1人，则不同的安排方案共有（）

A、150种 B、120种 C、240种 D、540种

查看试题解析
8. ${(x^{3} - \frac{2}{x})}^{n}$ 的二项展开式的各项系数的绝对值之和为729，则 ${(x - \frac{2}{x})}^{n}$ 展开式中的二次项的系数是（）

A、-60 B、60 C、-30 D、30

查看试题解析
9. 某群体中的每位成员使用移动支付的概率都为 $p$ ，各成员的支付方式相互独立，设 $X$ 为该群体的10位成员中使用移动支付的人数， $D X = 2.4$ ， $P (X = 4) < P (X = 6)$ ，则 $p =$ （）

A、0.7 B、0.6 C、0.4 D、0.3

查看试题解析
10. 一个盒子装有质地、大小、形状都相同的6个球，其中红球3个，黄球2个，蓝球1个.现从中任取两个球，记事件 $A$ ：“取出的两个球颜色不同”，事件 $B$ ：“取出一个红球，一个黄球”，则 $P (B | A) =$ （）

A、 $\frac{11}{15}$ B、 $\frac{1}{3}$ C、 $\frac{6}{11}$ D、 $\frac{2}{5}$

查看试题解析
11. 已知某超市为顾客提供四种结账方式：现金、支付宝、微信、银联卡.若顾客甲没有银联卡，顾客乙只带了现金，顾客丙、丁用哪种方式结账都可以，这四名顾客购物后，恰好用了其中的三种结账方式，那么他们结账方式的可能情况有（）种

A、19 B、7 C、26 D、12

查看试题解析
12. “三个臭皮匠，赛过诸葛亮”，这是我们常说的口头禅，主要是说集体智慧的强大. 假设李某智商较高，他独自一人解决项目M的概率为 $P_{1} = 0.3$ ；同时，有 $n$ 个水平相同的人也在研究项目M ，他们各自独立地解决项目M的概率都是 $0.1$ .现在李某单独研究项目M ，且这 $n$ 个人组成的团队也同时研究项目M ，设这个 $n$ 人团队解决项目M的概率为 $P_{2}$ ，若 $P_{2} \geq P_{1}$ ，则 $n$ 的最小值是（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

13. 设随机变量 $X \sim N (1 ， σ^{2})$ ，且 $P (X > 2) = \frac{1}{5}$ ，则 $P (0 < X < 1) =$ ．

查看试题解析
14. 若 $(3 + a x) {(1 + x)}^{4}$ 展开式中 $x$ 的系数为13，则展开式中各项系数和为（用数字作答）．

查看试题解析
15. 现用五种不同的颜色，要对如图中的四个部分进行着色，要求公共边的两块不能用同一种颜色，共有种不同着色方法

查看试题解析
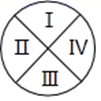16. 已知从装有 $n + 1$ 个球（其中 $n$ 个白球，1个黑球）的口袋中取出 $m$ 个球， $0 < m < n$ ， $m, n \in N$ ，共有 $C_{n + 1}^{m}$ 种取法，在这 $C_{n + 1}^{m}$ 种取法中，可以分成两类：一类是取出的 $m$ 个球全部为白球，另一类是取出1个黑球和 $(m - 1)$ 个白球，共有 $C_{1}^{0} C_{n}^{m} + C_{1}^{1} C_{n}^{m - 1}$ 种取法，即有等式 $C_{n}^{m} + C_{n}^{m - 1} = C_{n + 1}^{m}$ 成立，试根据上述思想，化简下列式子： $C_{n}^{m} + C_{k}^{1} C_{n}^{m - 1} + C_{k}^{2} C_{n}^{m - 2} + \cdot \cdot \cdot + C_{k}^{k} C_{n}^{m - k} =$ $(1 \leq k < m \leq n$ ， $k, m, n \in N)$

查看试题解析

三、解答题

17. 设 ${(1 + x)}^{n} = a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{n} x^{n}, n ⩾ 4, n \in N^{*}$ .已知 $a_{3}^{2} = 2 a_{2} a_{4}$ .

(1)、求n的值；

(2)、设 ${(1 + \sqrt{3})}^{n} = a + b \sqrt{3}$ ，其中 $a, b \in N^{*}$ ，求 $a^{2} - 3 b^{2}$ 的值.

查看试题解析
18. 某市举办数学知识竞赛活动，共5000名学生参加，竞赛分为初试和复试，复试环节共3道题，其中2道单选题，1道多选题，得分规则如下：参赛学生每答对一道单选题得2分，答错得0分，答对多选题得3分，答错得0分，答完3道题后的得分之和为参赛学生的复试成绩.

(1)、通过分析可以认为学生初试成绩 $X$ 服从正态分布 $N (μ ， σ^{2})$ ，其中 $μ = 66$ ， $σ^{2} = 144$ ，试估计初试成绩不低于90分的人数；

(2)、已知小强已通过初试，他在复试中单选题的正答率为 $\frac{2}{3}$ ，多选题的正答率为 $\frac{1}{2}$ ，且每道题回答正确与否互不影响.记小强复试成绩为 $Y$ ，求 $Y$ 的分布列及数学期望.
附： $P (μ - σ < X < μ + σ) = 0.6826$ ， $P (μ - 2 σ < X < μ + 2 σ) = 0.9544$ ， $P (μ - 3 σ < X < μ + 3 σ) = 0.9974$ .

查看试题解析

19. 《中华人民共和国民法总则》（以下简称《民法总则》）自2017年10月1日起施行.作为民法典的开篇之作，《民法总则》与每个人的一生息息相关.某地区为了调研本地区人们对该法律的了解情况，随机抽取50人，他们的年龄都在区间

[25, 85]

上，年龄的频率分布及了解《民法总则》的入数如下表：

年龄	$[25, 35)$	$[35, 45)$	$[45, 55)$	$[55, 65)$	$[65, 75)$	$[75, 85)$
频数	5	5	10	15	5	10
了解《民法总则》	1	2	8	12	4	5

参考公式和数据： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$

$P (K^{2} ⩾ k)$	0.050	0.010	0.001
$k$	3.841	6.635	10.828

(1)、填写下面

2 \times 2

列联表，并判断是否有99%的把握认为以45岁为分界点对了解《民法总则》政策有差异；

	年龄低于45岁的人数	年龄不低于45岁的人数	合计
了解	$a =$	$c =$
不了解	$b =$	$d =$
合计

(2)、若对年龄在

[45, 55)

，

[65, 75)

的被调研人中各随机选取2人进行深入调研，记选中的4人中不了解《民法总则》的人数为

X

，求随机变量的分布列和数学期望.

查看试题解析

20. 某景区的各景点从2009年取消门票实行免费开放后，旅游的人数不断地增加，不仅带动了该市淡季的旅游，而且优化了旅游产业的结构，促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变．下表是从2009年至2018年，该景点的旅游人数

y

（万人）与年份

x

的数据：

第x年	1	2	3	4	5	6	7	8	9	10
旅游人数y（万人）	300	283	321	345	372	435	486	527	622	800

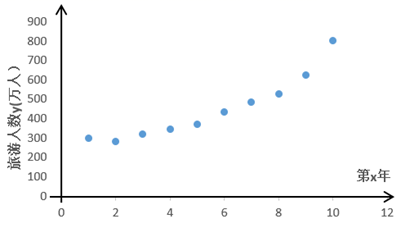
该景点为了预测2021年的旅游人数，建立了 $y$ 与 $x$ 的两个回归模型：

模型①：由最小二乘法公式求得 $y$ 与 $x$ 的线性回归方程 $\hat{y} = 50.8 x + 169.7$ ；

模型②：由散点图的样本点分布，可以认为样本点集中在曲线 $y = a e^{b x}$ 的附近．

参考公式、参考数据及说明：

①对于一组数据 $(v_{1} ， w_{1}) ， (v_{2} ， w_{2}) ， \dots ， (v_{n} ， w_{n})$ ，其回归直线 $\hat{w} = \hat{α} + \hat{β} v$ 的斜率和截距的最小二乘法估计分别为 $\hat{β} = \frac{\sum_{i = 1}^{n} (w_{i} - \bar{w}) (v_{i} - \bar{v})}{\sum_{i = 1}^{n} {(v_{i} - \bar{v})}^{2}} ， \hat{α} = \bar{w} - \hat{β} \bar{v}$ ．②刻画回归效果的相关指数 $\frac{b}{a} + \frac{a}{b} > 2 £ \neg \frac{c}{a} + \frac{a}{c} > 2 £ \neg \frac{c}{b} + \frac{b}{c} > 2$ ；③参考数据： $e^{5.46} \approx 235$ ， $e^{1.43} \approx 4.2$ ．

$\bar{x}$	$\bar{y}$	$\bar{u}$	$\sum_{i = 1}^{10} {(x_{i} - \bar{x})}^{2}$	$\sum_{i = 1}^{10} (x_{i} - \bar{x}) (y_{i} - \bar{y})$	$\sum_{i = 1}^{10} (x_{i} - \bar{x}) (u_{i} - \bar{u})$
$5.5$	449	6.05	83	4195	9.00

表中 $u_{i} = \ln y_{i} ， \bar{u} = \frac{1}{10} \sum_{i = 1}^{10} u_{i}$ ．

(1)、根据表中数据，求模型②的回归方程

\hat{y} = a e^{b x}

．（

a

精确到个位，

b

精确到0.01）．

(2)、根据下列表中的数据，比较两种模型的相关指数

R^{2}

，并选择拟合精度更高、更可靠的模型，预测2021年该景区的旅游人数（单位：万人，精确到个位）．

回归方程	① $y = 50.8 x + 169.7$	② $\hat{y} = a e^{b x}$
$\sum_{i = 1}^{10} {(y_{i} - \hat{y_{i}})}^{2}$	30407	14607

查看试题解析

21. 随着小汽车的普及，“驾驶证”已经成为现代人“必考”的证件之一.若某人报名参加了驾驶证考试，要顺利地拿到驾驶证，他需要通过四个科目的考试，其中科目二为场地考试.在一次报名中，每个学员有5次参加科目二考试的机会（这5次考试机会中任何一次通过考试，就算顺利通过，即进入下一科目考试；若5次都没有通过，则需重新报名），其中前2次参加科目二考试免费，若前2次都没有通过，则以后每次参加科目二考试都需要交200元的补考费.某驾校对以往2000个学员第1次参加科目二考试进行了统计，得到下表：

考试情况	男学员	女学员
第1次考科目二人数	1200	800
第1次通过科目二人数	960	600
第1次未通过科目二人数	240	200

若以上表得到的男、女学员第1次通过科目二考试的频率分别作为此驾校男、女学员每次通过科目二考试的概率，且每人每次是否通过科目二考试相互独立.现有一对夫妻同时在此驾校报名参加了驾驶证考试，在本次报名中，若这对夫妻参加科目二考试的原则为：通过科目二考试或者用完所有机会为止.

(1)、求这对夫妻在本次报名中参加科目二考试都不需要交补考费的概率；

(2)、若这对夫妻前2次参加科目二考试均没有通过，记这对夫妻在本次报名中参加科目二考试产生的补考费用之和为

X

元，求

X

的分布列与数学期望.

查看试题解析

22. 某单位计划在一水库建一座至多安装3台发电机的水电站，过去50年的水文资料显示，水库年入流量 $X$ （年入流量：一年内上游来水与库区降水之和，单位：亿立方米）都在40以上，不足80的年份有10年，不低于80且不超过120的年份有35年，超过120的年份有5年，将年入流量在以上三段的频率作为相应段的概率，假设各年的年入流量相互独立.

(1)、求未来3年中，设 $ξ$ 表示流量超过120的年数，求 $ξ$ 的分布列及期望；

(2)、水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量 $X$ 限制，并有如下关系：

年入流量 $X$

$40 < X < 80$

$80 \leq X \leq 120$

$X > 120$

发电机最多可运行台数

1

2

3

若某台发电机运行，则该台年利润为5000万元，若某台发电机未运行，则该台年亏损800万元，欲使水电站年总利润的均值达到最大，应安装发电机多少台？

查看试题解析

年入流量 $X$	$40 < X < 80$	$80 \leq X \leq 120$	$X > 120$
发电机最多可运行台数	1	2	3