初中数学浙教版七年级下学期期中复习专题7二元一次方程组

试卷更新日期：2021-04-08 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列方程组中不是二元一次方程组的是（）

A、 ${\begin{cases} s + 1 = 3 \\ 2 s - t = 4 \end{cases}$ B、 ${\begin{cases} m + n = 3 \\ 2 m - n = 4 \end{cases}$ C、 ${\begin{cases} x = 3 \\ y = 4 \end{cases}$ D、 ${\begin{cases} x + y = 3 \\ 2 x y - y = 4 \end{cases}$

查看试题解析
2. 下列二元一次方程组中，以 ${\begin{array}{l} x = 1 \\ y = - 2 \end{array}$ 为解的是（）

A、 ${\begin{array}{l} x + y = - 1 \\ 2 x - 3 y = - 4 \end{array}$ B、 ${\begin{array}{l} x - y = - 1 \\ 2 x + 3 y = 4 \end{array}$ C、 ${\begin{array}{l} x - y = - 1 \\ 2 x - 3 y = 4 \end{array}$ D、 ${\begin{array}{l} x + y = - 1 \\ 2 x + 3 y = - 4 \end{array}$

查看试题解析
3. 若方程组 ${\begin{array}{l} a + 2 b = 4 \\ 3a + 2b = 8 \end{array}$ ，则a+b等于（）

A、3 B、4 C、2 D、1

查看试题解析
4. 已知方程组 ${\begin{array}{l} x + 2 y - 5 = 0 \\ x + y + m = 0 \end{array}$ 和方程组 ${\begin{array}{l} 2 x + y + 8 = 0 \\ x + y + m = 0 \end{array}$ 有相同的解，则 $m$ 的值是（）

A、1 B、 $- 1$ C、2 D、 $- 2$

查看试题解析
5. 已知关于x ， y的方程组 ${\begin{array}{l} 2 x - 3 y = 4 \\ a x + b y = 2 \end{array}$ ，与 ${\begin{array}{l} 3 x - 5 y = 6 \\ b x + a y = - 4 \end{array}$ ，有相同的解，则a ， b的值为（）

A、 ${\begin{array}{l} a = - 2 \\ b = 1 \end{array}$ B、 ${\begin{array}{l} a = 1 \\ b = - 2 \end{array}$ C、 ${\begin{array}{l} a = 1 \\ b = 2 \end{array}$ D、 ${\begin{array}{l} a = - 1 \\ b = - 2 \end{array}$

查看试题解析
6. 已知 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ 是二元一次方程组 ${\begin{array}{l} 3 x + 2 y = m \\ m x - y = n \end{array}$ 的解，则m﹣n的值为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 已知关于x，y的方程组 ${\begin{array}{l} 3 x - 5 y = 2 a \\ x - 2 y = a - 5 \end{array}$ ，则下列结论中正确的是（）
①当a＝5时，方程组的解是 ${\begin{array}{l} x = 10 \\ y = 20 \end{array}$ ；②当x，y的值互为相反数时，a＝20；③当 $2^{x} \cdot 2^{y} = 16$ 时，a＝18；④不存在一个实数a使得x=y.

A、①②④ B、②③④ C、②③ D、②④

查看试题解析
8. 若方程组 ${\begin{matrix} 2 a - 3 b = 13 \\ 3 a + 5 b = 30 \end{matrix}$ 的解是 ${\begin{matrix} a = 8.3 \\ b = 1.2 \end{matrix}$ ，则方程组 ${\begin{matrix} 2 (x + 2) - 3 (y - 1) = 13 \\ 3 (x + 2) + 5 (y - 1) = 30 \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 8.3 \\ y = 1.2 \end{matrix}$ B、 ${\begin{matrix} x = 10.3 \\ y = 0.2 \end{matrix}$ C、 ${\begin{matrix} x = 6.3 \\ y = 2.2 \end{matrix}$ D、 ${\begin{matrix} x = 10.3 \\ y = 0.2 \end{matrix}$

查看试题解析
9. 如果方程组 ${\begin{cases} 2 x + y = □ \\ x - 2 y = 3 \end{cases}$ 的解为 ${\begin{cases} x = 5 \\ y = △ \end{cases}$ ，那么“□”和“△”所表示的数分别是（）

A、14，4 B、11，1 C、9，-1 D、6，-4

查看试题解析
10. 有下列说法：
①在同一平面内，过直线外一点有且只有一条直线与已知直线平行；②无论k取任何实数，多项式 $x^{2} - k y^{2}$ 总能分解成两个一次因式积的形式；③若 ${(t - 3)}^{3 - 2 t} = 1$ ，则 $t$ 可以取的值有3个；④关于 $x$ ， $y$ 的方程组为 ${\begin{array}{l} a x + 2 y = - 5 \\ - x + a y = 2 a \end{array}$ ，将此方程组的两个方程左右两边分别对应相加，得到一个新的方程，当 $a$ 每取一个值时，就有一个确定的方程，而这些方程总有一个公共解，则这个公共解是 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ .其中正确的说法是 $($ $)$

A、①④ B、①③④ C、②③ D、①②

查看试题解析

二、填空题

11. 已知方程组 ${\begin{cases} 3 a + b = 4 \\ a - 2 b = 1 \end{cases}$ ，则2a+3b的值是。

查看试题解析
12. 已知关于x、y的方程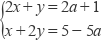的解满足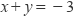，则a的值为.

查看试题解析
13. 一个关于x、y的二元一次方程组的解是 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ ，这样的方程组可以是；（只要求写出一个）

查看试题解析
14. 若关于x，y的二元一次方程组 ${\begin{cases} x + y = 2 \\ A = 0 \end{cases}$ 的解为 ${\begin{cases} x = 1 \\ y = 1 \end{cases}$ ，则多项式A可以是(写出一个即可)。

查看试题解析
15. 已知 ${\begin{cases} x = 2 \\ y = 1 \end{cases}$ 是方程组 ${\begin{cases} m x - y = 1 \\ x - n y = 3 \end{cases}$ 的解，则（m﹣n）³＝.

查看试题解析
16. 已知关于 $x, y$ 的方程组 ${\begin{array}{l} x - y = 2 a \\ 3 x + y = 3 a - 15 \end{array}$ 的解互为相反数，则常数a的值为.

查看试题解析
17. 若方程组 ${\begin{matrix} 3 x + 4 y = 12.5 \\ 2 x + 5 y = 13 \end{matrix}$ 的解是 ${\begin{matrix} x = 1.5 \\ y = 2 \end{matrix}$ ，请求出方程组 ${\begin{matrix} 3 (m - 5) + 4 (n + 3) = 12.5 \\ 2 (m - 5) + 4 (n + 3) = 13 \end{matrix}$ 中m，n的值，m＝， n＝.

查看试题解析
18. 已知关于x，y的二元一次方程组 ${\begin{array}{l} a x + b y = 7 \\ b x + a y = 8 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ ，那么关于m，n的二元一次方程组 ${\begin{array}{l} a (m + n) + b (m - n) = 7 \\ b (m + n) + a (m - n) = 8 \end{array}$ 的解为．

查看试题解析

三、计算题

19. a取何值时(a为整数），方程组 ${\begin{array}{l} 2 x + a y = 4 \\ x - 2 y = 0 \end{array}$ 的解是正整数，并求这个方程组的解．

查看试题解析
20. 已知方程组 ${\begin{array}{l} x - y = m + 3 \\ x + 3 y = m \end{array}$ 中的x、y互为相反数，则m的值为多少？

查看试题解析
21. m为正整数，已知二元一次方程 ${\begin{matrix} m x + 2 y = 10 ① \\ 3 x - 2 y = 0 ② \end{matrix}$ 有整数解，即x，y均为整数，求m的值及方程组的解．

查看试题解析
22. 若方程组 ${\begin{array}{l} 2 x - y - 4 m = 0 \\ 14 x - 3 y = 20 \end{array}$ 的解中 $y$ 值是 $x$ 值的3倍，求 $m$ 的值.

查看试题解析
23. 若方程组 ${\begin{matrix} x + a y = 0 \\ x + y = 1 \end{matrix}$ 的解是 ${\begin{matrix} x = 0.5 \\ y = ▲ \end{matrix}$ ，其中y的值被盖住了，求a的值．

查看试题解析
24. 甲、乙两人共同解方程组 ${\begin{array}{l} a x + 5 y = 15 ① \\ 4 x - b y = - 2 ② \end{array}$ ，由于甲看错了方程①中的a，得到方程组的解为 ${\begin{array}{l} x = - 3 \\ y = - 1 \end{array}$ ，乙看错了方程②中的b，得到方程组的解为 ${\begin{array}{l} x = 5 \\ y = 4 \end{array}$ ，试计算a²⁰¹⁹+（﹣ $\frac{1}{10}$ b）²⁰¹⁸ ．

查看试题解析
25. 已知关于x，y的方程组：（1） ${\begin{matrix} 2 a + 5 y = - 6 \\ a x - b y = - 4 \end{matrix}$ 与方程组（2） ${\begin{matrix} x - 4 y = 23 \\ b x + a y = 8 \end{matrix}$ 的解x，y的值刚好交换了位置，试求a，b的值及每一个方程组的解．

查看试题解析
26. 计算：

(1)、已知a-3b=2a+b-15=1，求代数式a²-4ab+b²+3的值.

(2)、已知方程组 ${\begin{cases} 2 x + a y = 3, \\ 4 x + 6 y = 2 - b \end{cases}$ 有无数多组解，求a,b的值.

查看试题解析