初中数学浙教版七年级下学期期中复习专题10三元一次方程组及其解法

试卷更新日期：2021-04-08 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列方程组中，是三元一次方程组的是（）

A、 ${\begin{array}{l} x + y = 0 \\ y + z = 1 \\ z + w = 5 \end{array}$ B、 ${\begin{array}{l} x + y = 0 \\ y + 2 x = 1 \end{array}$ C、 ${\begin{array}{l} 3 x + 4 z = 7 \\ 2 x + 3 y = 9 - z \\ 5 x - 9 y + 7 z = 8 \end{array}$ D、 ${\begin{array}{l} x^{2} - 2 y = 0 \\ y + z = 3 \\ x + y + z = 1 \end{array}$

查看试题解析
2. 三元一次方程组 ${\begin{array}{l} x + y = 3 \\ y + z = 5 \\ x + z = 4 \end{array}$ ，的解为（）

A、 ${\begin{array}{l} x = 1 \\ y = 3 \\ z = 2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 1 \\ z = 3 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = 2 \\ z = 1 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 2 \\ z = 3 \end{array}$

查看试题解析
3. 三元一次方程组 ${\begin{array}{l} 2 x = 3 y = 6 z \\ x + 2 y + z = 16 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 1 \\ y = 3 \\ z = 5 \end{array}$ B、 ${\begin{array}{l} x = 6 \\ y = 3 \\ z = 2 \end{array}$ C、 ${\begin{array}{l} x = 6 \\ y = 4 \\ z = 2 \end{array}$ D、 ${\begin{array}{l} x = 4 \\ y = 5 \\ z = 6 \end{array}$

查看试题解析
4. 解三元一次方程组 ${\begin{cases} x - y + z = - 3 ， ① \\ x + 2 y - z = 1 ， ② \\ x + y = 0 ， ③ \end{cases}$ 要使解法较为简便，首先应进行的变形为（）

A、①+② B、①-② C、①+③ D、②-③

查看试题解析
5.
为迎接2013年“亚青会”，学校组织了一次游戏：每位选手朝特制的靶子上各投三以飞镖，在同一圆环内得分相同．如图所示，小明、小君、小红的成绩分别是29分、43分和33分，则小华的成绩是（）

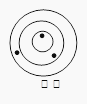A、31分 B、33分 C、36分 D、38分

查看试题解析
6. 某校一年级有64人，分成甲、乙、丙三队，其人数比为4：5：7．若由外校转入1人加入乙队，则后来乙与丙的人数比为何（）

A、3：4 B、4：5 C、5：6 D、6：7

查看试题解析
7. 在抗击疫情网络知识竞赛中，为奖励成绩突出的学生，学校计划用200元钱购买A、B、C三种奖品，A种每个10元，B种每个20元，C种每个30元，在C种奖品不超过两个且钱全部用完的情况下，有多少种购买方案（）

A、12种 B、15种 C、16种 D、14种

查看试题解析
8. 某单位在一快餐店订了22盒盒饭，共花费140元，盒饭共有甲、乙、丙三种，它们的单价分别为8元、5元、3元．那么可能的不同订餐方案有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 已知方程组 ${\begin{array}{l} x + y = 3 \\ y + z = - 2 \\ z + x = 9 \end{array}$ ，则x＋y＋z的值为（）

A、6 B、－6 C、5 D、－5

查看试题解析
10. 我国古代数学家张丘建在《张丘建算经）里，提出了“百钱买百鸡”这个有名的数学问题.用100个钱买100只鸡，公鸡每只五个钱，母鸡每只三个钱，小鸡每个钱三只.问公鸡，小鸡各买了多少只？在这个问题中，小鸡的只数不可能是（）

A、87 B、84 C、81 D、78

查看试题解析

二、填空题

11. “九九重阳节，浓浓敬老情”，今年某花店在重阳节推出“松鹤长春”“欢乐远长”“健康长寿”三种花束.“松鹤长春”花束中有8枝百合，16 枝康乃馨；“欢乐远长”花束中有6枝百合，16枝康乃馨，2枝剑兰；“健康长寿”花束中有4枝百合，12枝康乃馨，2枝剑兰.已知百合花每枝1元，康乃馨每枝 $\frac{3}{4}$ 元，剑兰每枝5元，重阳节当天销售这三种花束共2549元，其中百合花的销售额为458元，则剑兰的销售量为枝.

查看试题解析
12. 设 ${\begin{array}{l} 2 x + y + 3 z = 23 \\ x + 4 y + 5 z = 36 \end{array}$ ，则3x-2y+z= ．

查看试题解析
13. 在刚刚结束的万州二中秋季运动会中，有一个趣味项目，5分钟内运送三大筐数量相同的兵乓球，甲每次从第一个大筐中取出9个球；乙每次从第二个大筐中取出7个球；丙则是每次从第三个大筐中取出5个球.比赛激烈最终三人都记不清各自取了多少次球了，最后裁判清点发现第一个筐中剩下7个球，第二个筐剩下4个球，第三个筐剩下2个球，那么根据上述情况可以推知每个筐中至少有个兵乓球.

查看试题解析
14. 已知关于x、y的方程 ${\begin{array}{l} 2 x + y = 2 a + 1 \\ x + 2 y = 5 - 5 a \end{array}$ 的解满足 $x + y = - 3$ ，则a的值为.

查看试题解析
15. 有A、B、C三种商品，如果购5件A、2件B、3件C共需513元，购3件A、6件B、5件C共需375件，那么购A、B、C各一件共需元.

查看试题解析
16. 为防控新冠疫情，做好个人防护，小君去药店购买口罩，若买6个平面口罩和4个 $K N 95$ 口罩，则她所带的钱还剩下10元；若买4个平面口罩和6个 $K N 95$ 口罩，则她所带的钱还缺8元，若只买10个 $K N 95$ 口罩，则她所带的钱还缺元.

查看试题解析
17. 为确保信息安全，在传输时往往需加密，发送方发出一组密码a，b，c时，则接收方对应收到的密码为A，B，C，双方约定：A＝2a－b，B＝2b，C＝b＋c，例如发出的密码是1，2，3，则收到的密码是0，4，5.若接收方收到的密码是2，8，11时，则发送方发出的密码是

查看试题解析
18. 火锅是重庆的一张名片，深受广大市民的喜爱.重庆某火锅店采取堂食、外卖、店外摆摊（简称摆摊）三种方式经营，6月份该火锅店堂食、外卖、摆摊三种方式的营业额之比为3：5：2.随着促进消费政策的出台，该火锅店老板预计7月份总营业额会增加，其中摆摊增加的营业额占总增加的营业额的，则摆摊的营业额将达到7月份总营业额的，为使堂食、外卖7月份的营业额之比为8：5，则7月份外卖还需增加的营业额与7月份总营业额之比是.

查看试题解析

三、计算题

19. 解方程组：

(1)、 ${\begin{cases} x = 3 + 2 y \\ 3 x - 8 y = 13 \end{cases}$

(2)、 ${\begin{cases} x + y + z = 12 \\ x + 2 y - z = 6 \\ 3 x - y + z = 10 \end{cases}$ ．

查看试题解析
20. $\{\begin{matrix} x + 2 y + 3 z = 15 \\ \frac{x + 4 z}{3} = \frac{y - 3 z}{4} = 3 \end{matrix}$

查看试题解析
21. 已知x ， y ， z都不为零，且满足4x－3y－6z＝0，x＋2y－7z＝0．求 $\frac{2 x - 3 y + z}{3 x + y - 5 z}$ 的值.

查看试题解析
22. 已知 ${\begin{cases} 3 x + y + 2 z = 2 \\ 2 x + y + 3 z = - 11 \\ x - y - 4 z = - 10 \end{cases}$ 试解关于m、n的方程组 ${\begin{cases} x + m = y + n \\ z + 2 n = y + m \end{cases}$

查看试题解析
23. 已知 ${\begin{matrix} x + 4 y - 3 z = 0 \\ 4 x - 5 y + 2 z = 0 \end{matrix}$ ，xyz≠0，求 $\frac{3 x^{2} + 2 x y + z^{2}}{x^{2} + y^{2}}$ 的值．

查看试题解析
24. 一个三位数，如果把它的个位数字与百位数字交换位置，那么所得的新数比原数小99，且各位数字之和为14，十位数字是个位数字与百位数字之和．求这个三位数．

查看试题解析
25. 列方程（组），解应用题.
根据图中的信息，求桌子的高.

查看试题解析
26. 有一场足球比赛，共有九支球队参加，采取单循环赛，其记分和奖励方案如下表：

标准

胜一场

平一场

负一场

积分

3

1

0

奖励（元／人）

2000

800

0

甲队参加完了全部8场比赛，共得积分16分．

(1)、求甲队胜负的所有可能情况；

(2)、若每一场比赛，每一个参赛队员均可得出场费500元，求甲队参加了所有8场比赛的队员的个人总收入（奖金加上出场费）．

查看试题解析

标准	胜一场	平一场	负一场
积分	3	1	0
奖励（元／人）	2000	800	0