初中数学浙教版七年级下学期期中复习专题4 平行线的性质
试卷更新日期：2021-04-08 类型：复习试卷
一、单选题
-
1. 如图，已知a∥b，l与a，b相交.若∠1＝70°，则∠2等于（ ）
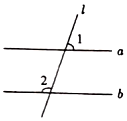A、.120° B、110° C、.100° D、.70°2. 如图，已知平行线a，b，一个直角三角板的直角顶点在直线a上，另一个顶点在直线b上，若 ，则 的大小为（ ）
A、 B、 C、 D、3. 如图，若直线 ，则下列各式成立的是（ ）
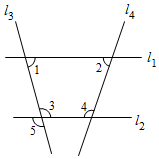A、 B、 C、 D、4. 如图，下列推理错误的是（ ）
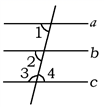A、∵ ， B、∵ C、 D、∵5. 如图，已知 ，则下列结论中正确的是（ ）
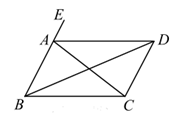A、 B、 C、 D、6. 如图，AB∥CD，∠BAE＝120°，∠DCE＝30°，则∠AEC＝（ ）度．
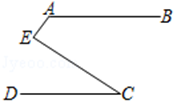A、70 B、150 C、90 D、1007. 若一副三角板按如图所示放置，则∠EGA的度数为（ ）
A、30° B、45° C、60° D、75°8. 如图，由AB∥CD，可以得到（ ）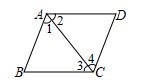
A、∠1＝∠2 B、∠2＝∠3 C、∠1＝∠4 D、∠3＝∠49. 如图，三角板的直角顶点落在矩形纸片的一边上.若 ，则 的度数是（ ）
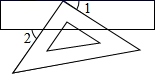A、 B、 C、 D、10. 如图，AB∥CD，∠EFD＝64°，∠FEB的角平分线EG交CD于点G，则∠GEB的度数为（ ）
A、66° B、56° C、68° D、58°二、填空题
-
11. 一大门的栏杆如图所示，BA垂直地面AE于点A，CD平行于地面AE，则∠ABC+∠BCD＝.
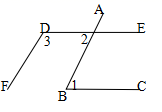
12. 如图， ，若 ，则 的度数为.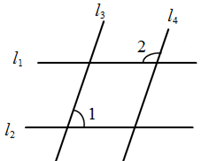
13. 如图，直线 ， ， ，点 在直线 上， ，若 ，则 的度数为.
14. 如图，已知AB∥CD，∠1：∠2：∠3=1：2：3，则∠EBA的度数为 ．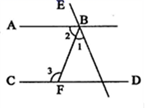
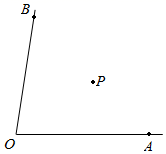
15. 在同一平面内， 与 的两边分别平行，若 ，则 的度数为16. 如图，AB∥CD，CE∥GF，若∠1＝60°，则∠2＝°.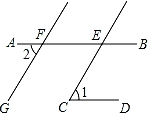
17. 如图所示，C岛在A岛的北偏东50°方向，C岛在B岛的北偏西40°方向，则从C岛看A、B两岛的视角∠ACB等于.
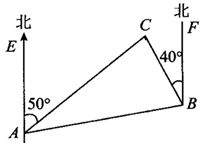18. 如果在某建筑物的A处测得目标B的俯角为37°，那么从目标B可以测得这个建筑物的A处的仰角为 ．三、计算题
-
19. 如图， ， ， ，求 、 的度数．
20. 已知：如图， ，求证： .
四、解答题
-
21. 如图，已知∠A=∠C，AB∥CD.那么∠E与∠F相等吗？请说明理由.
22. 如图，∠ABC与∠DEF的两边分别交于点M、N.若∠ABC＝∠DEF，且AB∥EF.试说明BC∥DE.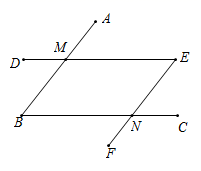
23. 补全解答过程：如图，EF∥AD，∠1=∠2，若∠BAC=70°，求∠AGD.
解：∵EF∥AD，（已知）
∴∠2= ， （两直线平行，同位角相等）.
又∵∠1=∠2，（已知）
∴∠1=∠3，（等量代换）
∴AB∥ ， （）
∴∠AGD＋∠BAC=180°.（）
∵∠BAC=70°，（已知）
∴∠AGD= .
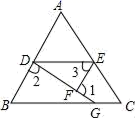
24. 完成下面的证明：如图，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，连接DE，DF，DE∥AB，∠BFD＝∠CED，连接BE交DF于点G，求证：∠EGF+∠AEG＝180°．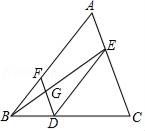
证明：∵DE∥AB（已知），
∴∠A＝∠CED（）
又∵∠BFD＝∠CED（已知），
∴∠A＝∠BFD（）
∴DF∥AE（）
∴∠EGF+∠AEG＝180°（）
五、作图题
