山东省日照市莒县2019-2020学年高二下学期数学期中过程性测试试卷

试卷更新日期：2021-04-07 类型：期中考试

进入出卷网下载

一、单选题

1. 下列求导运算正确的是（）

A、 ${(x + \frac{3}{x})}^{'} = 1 + \frac{3}{x^{2}}$ B、 ${(\log_{2} x)}^{'} = \frac{1}{x \ln 2}$ C、 ${(3^{x})}^{'} = 3^{x}$ D、 ${(x^{2} \cos x)}^{'} = - 2 x \sin x$

查看试题解析
2. 公园有4个门，从一个门进，另一个门出，则不同的走法的种数为（）

A、16 B、13 C、12 D、10

查看试题解析
3. 生物实验室有5只兔子，其中只有3只测量过某项指标。若从这5只兔子中随机取出3只，则恰有2只测量过该指标的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{5}$ C、 $\frac{2}{5}$ D、 $\frac{1}{5}$

查看试题解析
4. 3名男生､3名女生排成一排，男生必须相邻，女生也必须相邻的排法种数为（）

A、2 B、9 C、72 D、36

查看试题解析
5. 甲、乙两人参加“社会主义价值观”知识竞赛，甲、乙两人的能荣获一等奖的概率分别为 $\frac{2}{3}$ 和 $\frac{3}{4}$ ，甲、乙两人是否获得一等奖相互独立，则这两个人中恰有一人获得一等奖的概率为（）

A、 $\frac{3}{4}$ B、 $\frac{2}{3}$ C、 $\frac{5}{7}$ D、 $\frac{5}{12}$

查看试题解析
6. 已知盒中装有3个红球、2个白球、5个黑球，它们大小形状完全相同，现需一个红球，甲每次从中任取一个不放回，在他第一次拿到白球的条件下，第二次拿到红球的概率（）

A、 $\frac{3}{10}$ B、 $\frac{1}{3}$ C、 $\frac{3}{8}$ D、 $\frac{2}{9}$

查看试题解析
7. 函数 f(x)=(x−3)e^x 的单调递增区间是（）

A、 $(- \infty ， 2)$ B、 $(0 ， 3)$ C、 $(1 ， 4)$ D、 $(2 ， + \infty)$

查看试题解析
8. 点P是曲线x²﹣y﹣2ln $\sqrt{x}$ =0上任意一点，则点P到直线4x+4y+1=0的最小距离是（）

A、 $\frac{\sqrt{2}}{2}$ (1-ln2) B、 $\frac{\sqrt{2}}{2}$ ( $\frac{1}{2}$ +ln2) C、 $\frac{\sqrt{2}}{2}$ (1+ln2) D、 $\frac{1}{2}$ (1+ln2)

查看试题解析

二、多选题

9. 已知函数 $y = f (x)$ 的导函数 $f^{'} (x)$ 的图象如图所示，则下列判断正确的是（）

A、函数 $y = f (x)$ 在区间 $(- 3 ， - \frac{1}{2})$ 内单调递增 B、当 $x = - 2$ 时，函数 $y = f (x)$ 取得极小值 C、函数 $y = f (x)$ 在区间 $(- 2 ， 2)$ 内单调递增 D、当 $x = 3$ 时，函数 $y = f (x)$ 有极小值

查看试题解析
10. 已知二项式 ${(2 x - \frac{1}{\sqrt{x}})}^{n} (n \in N^{*})$ 的展开式中第2项与第3项的二项式系数之比是 $2 : 5$ ，则下列说法正确的是（）

A、所有项的系数之和为1 B、所有项的系数之和为-1 C、含 $x^{3}$ 的项的系数为240 D、含 $x^{3}$ 的项的系数为-240

查看试题解析
11. 甲､乙两类水果的质量(单位： $kg$ )分别服从正态分布 $N (μ_{1} ， σ_{1}^{2}) ， N (μ_{2} ， σ_{2}^{2})$ ，其正态分布的密度曲线 $f (x) = \frac{1}{\sqrt{2 π} \cdot σ} e^{- \frac{{(x - μ)}^{2}}{2 σ^{2}}} ， x \in R ，$ 如图所示，则下列说法正确的是（）

A、甲类水果的平均质量 $μ_{1} = 0.4 kg$ B、甲类水果的质量比乙类水果的质量更集中于平均值左右 C、甲类水果的平均质量比乙类水果的平均质量小 D、乙类水果的质量服从的正态分布的参数 $σ_{2}^{} = 1.99$

查看试题解析
12. 下列不等式正确的有（）

A、 $\ln 3 < \sqrt{3} \ln 2$ B、 $\ln π < \sqrt{\frac{π}{e}}$ C、 $2^{\sqrt{15}} < 15$ D、 $e \ln 2 < 2$

查看试题解析

三、填空题

13. 已知随机变量 $ξ$ 服从二项分布， $ξ ~ B (6, \frac{1}{2})$ ，则 $E (2 ξ + 3) =$ ， $D (2 ξ + 3) =$ .

查看试题解析
14. 函数 $f (x) = \frac{1}{3} x^{3} - 4 x + 4$ 的极大值为.

查看试题解析
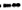15. 《易经》是中国传统文化中的精髓，下图是易经八卦图（含乾、坤、巽、震、坎、离、艮、兑八卦），每卦有三根线组成（“ ”表示一根阳线，“ ”表示一根阴线），从八卦中任取两卦，这两卦的六根线中恰有三根阳线和三根阴线的概率．

查看试题解析
16. 已知函数 $f (x) = (k x - 2) e^{x} - x (x > 0)$ ，若 $f (x) < 0$ 的解集为 $(s ， t)$ ，且 $(s ， t)$ 中恰有两个整数，则实数 $k$ 的取值范围为.

查看试题解析

四、解答题

17. 已知二项式 ${(x^{2} + \frac{2}{\sqrt{x}})}^{n}$ 的展开式中第五项为常数项.

(1)、求展开式中二项式系数最大的项；

(2)、求展开式中有理项的系数和.

查看试题解析
18. 已知函数 $f (x) = e^{x} \cos x - x$ ．
（Ⅰ）求曲线 $y = f (x)$ 在点 $(0 ， f (0))$ 处的切线方程；

（Ⅱ）求函数 $f (x)$ 在区间 $[0 ， \frac{π}{2}]$ 上的最大值和最小值．

查看试题解析
19. 男运动员6名，女运动员4名，其中男､女队长各1名.现选派5人外出参加比赛，在下列情形中各有多少种选派方法？

(1)、男运动员3名，女运动员2名；

(2)、队长中至少有1人参加；

(3)、既要有队长，又要有女运动员.

查看试题解析
20. 已知 $x = 1$ 是 $f (x)=2 x + \frac{b}{x} + \ln x$ 的一个极值点.

(1)、求函数 $f (x)$ 的单调递减区间；

(2)、设函数 $g (x) = f (x) - \frac{3 + a}{x}$ ，若函数 $g (x)$ 在区间 $[1 ， 2]$ 内单调递增，求 $a$ 的取值范围.

查看试题解析
21. 为加快推进我区城乡绿化步伐，植树节之际，决定组织开展职工义务植树活动，某单位一办公室现安排4个人去参加植树活动，该活动有甲､乙两个地点可供选择.约定：每个人通过掷一枚质地均匀的骰子决定自己去哪个地点植树，掷出点数为1或2的人去甲地，掷出点数大于2的人去乙地.

(1)、求这4个人中恰有2人去甲地的概率；

(2)、求这4个人中去甲地的人数大于去乙地的人数的概率；

(3)、用 $X, Y$ 分别表示这4个人中去甲､乙两地的人数，记 $ξ = | X - Y |$ ，求随机变量 $ξ$ 的分布列与数学期望 $E (ξ)$ .

查看试题解析
22. 已知函数 $f (x) = (x + 1) \ln (x + 1) - \frac{1}{2} a x^{2} - x$ （ $a \in R$ ）.
（Ⅰ）设 $f^{'} (x)$ 为函数 $f (x)$ 的导函数，求函数 $f^{'} (x)$ 的单调区间；

（Ⅱ）若函数 $f (x)$ 在 $(0 ， + \infty)$ 上有最大值，求实数 $a$ 的取值范围.

查看试题解析