山东省临沂市兰陵县2019-2020学年高二下学期数学期中考试（5月）试卷

试卷更新日期：2021-04-07 类型：期中考试

进入出卷网下载

一、单选题

1. 设复数 $z$ 满足 $z (2 + i) = 5$ ，则 $| z - i | =$ （）

A、 $\sqrt{2}$ B、2 C、 $2 \sqrt{2}$ D、4

查看试题解析
2. 函数 $f (x) = c o s x (s i n x + 1)$ 的导数是（）．

A、 $c o s 2 x + s i n x$ B、 $c o s 2 x - s i n x$ C、 $c o s 2 x + c o s x$ D、 $c o s 2 x - c o s x$

查看试题解析
3. ${(1 + y)}^{n}$ 的展开式中，所有的二项式系数之和等于512，则第3项是（）

A、 $C_{9}^{3} y^{3}$ B、 $C_{9}^{2} y^{2}$ C、 $C_{8}^{3} y^{3}$ D、 $C_{8}^{2} y^{2}$

查看试题解析
4. 已知随机变量 $ξ + η = 8$ ，若 $ξ \sim B (10 ， 0.4)$ ，则 $E (η)$ ， $D (η)$ 分别是（）

A、4和2.4 B、2和2.4 C、6和2.4 D、4和5.6

查看试题解析
5. 甲、乙、丙、丁、戊五位同学站成一排照相，其中要求甲和乙必须相邻，且丙不能排最左端，则不同的排法共有（）

A、12种 B、24种 C、36种 D、48种

查看试题解析
6. 一个盒子里装有3种颜色，大小形状质地都一样的12个球，其中黄球5个，蓝球4个，绿球3个，现从盒子中随机取出两个球，记事件A“取出的两个球颜色不同”，事件B“取出一个黄球，一个蓝球”，则 $P (B | A) =$ （）

A、 $\frac{12}{47}$ B、 $\frac{15}{47}$ C、 $\frac{20}{47}$ D、 $\frac{2}{11}$

查看试题解析
7. 同时抛掷5枚均匀的硬币80次，设5枚硬币正好出现2枚正面向上，3枚反面向上的次数为 $X$ ，则 $X$ 的均值为（）

A、20 B、25 C、30 D、40

查看试题解析
8. 已知函数 $f (x)$ 的导函数为 $f^{'} (x)$ ，且满足 $f (x) = 2 x f^{'} (1) + \ln x$ ，则 $f (1) =$ （）

A、 $- e$ B、 $e$ C、2 D、-2

查看试题解析

二、多选题

9. 若 ${(1 + m x)}^{8} = a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{8} x^{8}$ 且 $a_{1} + a_{2} + \dots + a_{8} = 255$ ，则实数m的值可以为（）

A、 $-$ 3 B、 $-$ 1 C、0 D、1

查看试题解析
10. 如图所示的折线图为某小区小型超市今年1月份到5月份的营业额和支出数据（利润=营业额－支出），根据折线图，下列说法正确的是（）

A、该超市这五个月中的营业额一直在增长； B、该超市这五个月的利润一直在增长； C、该超市这五个月中五月份的利润最高； D、该超市这五个月中的营业额和支出呈正相关．

查看试题解析
11. 给出以下四个说法，其中正确的说法是（）

A、残差点分布的带状区域的宽度越窄相关指数越小； B、在刻画回归模型的拟合效果时，相关指数 $R^{2}$ 的值越大，说明拟合的效果越好； C、在回归直线方程 $\hat{y} = 0.2 x + 12$ 中，当解释变量 $x$ 每增加一个单位时，预报变量 $\hat{y}$ 平均增加0.2个单位； D、对分类变量 $X$ 与 $Y$ ，若它们的随机变量 $K^{2}$ 的观测值 $k$ 越小，则判断“ $X$ 与 $Y$ 有关系”的把握程度越大．

查看试题解析
12. 已知函数 $f (x)$ 的定义域为[－1，5]，部分对应值如下表， $f (x)$ 的导函数 $y = f^{'} (x)$ 的图象如图所示，下列关于 $f (x)$ 的命题正确的是（）

$x$

$- 1$

0

4

5

$f (x)$

1

2

2

1

A、函数 $f (x)$ 的极大值点为0，4； B、函数 $f (x)$ 在[0，2]上是减函数； C、如果当 $x \in [- 1 ， t]$ 时， $f (x)$ 的最大值是2，那么 $t$ 的最大值为4； D、函数 $y = f (x) - a$ 的零点个数可能为0、1、2、3、4个．

查看试题解析

三、填空题

13. 计算： $A_{3}^{3} + C_{5}^{3} + \frac{5!}{6} =$

查看试题解析
14. 若曲线 $f (x) = \frac{1}{2} x^{2} - a \ln x$ 在点 $(1 ， f (1))$ 处的切线与直线 $x + 3 y + 1 = 0$ 垂直，则常数 $a =$ .

查看试题解析
15. 设 $0 < P < 1$ ，若随机变量 $ξ$ 的分布列是：

$ξ$

0

1

2

$P$

$\frac{P}{2}$

$\frac{1}{2}$

$\frac{1 - P}{2}$

则当 $P$ 变化时， $D (ξ)$ 的最大值是．

查看试题解析
16. 为了解高三复习备考情况，某校组织了一次阶段考试，若高三全体考生的数学成绩近似服从正态分布 $N (100 ， {17.5}^{2})$ ，已知成绩117以上（含117）的学生有80人，则此次参加考试的学生成绩不超过82的概率为，如果成绩大于135分的为特别优秀，那么本次考试数学成绩特别优秀的大约有人．
参考数据： $P (μ - σ < x < μ + σ) = 0.68$ ， $P (μ - 2 σ < x < μ + 2 σ) = 0.96$

查看试题解析

四、解答题

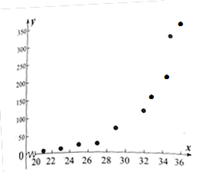
17. 已知复数 $z = (a^{2} - 4) + (a + 2) i$ ， $a \in R$ ．

(1)、若 $z$ 为纯虚数，求实数 $a$ 的值；

(2)、若 $z$ 在复平面上对应的点在直线 $x + 2 y + 1 = 0$ 上，求实数 $a$ 的值．

查看试题解析
18. 已知 ${(2 x + \frac{1}{\sqrt{x}})}^{n}$ 展开式前三项的二项式系数和为22．

(1)、求 $n$ 的值；

(2)、求展开式中的常数项；

(3)、求展开式中二项式系数最大的项．

查看试题解析

19. 经观测，某昆虫的产卵数

y

与温度

x

有关，现将收集到的温度

x_{i}

和产卵数

y_{i} (i = 1 ， 2 ， \dots ， 10)

的10组观测数据作了初步处理，得到如图的散点图及一些统计量表．

$\sum_{i = 1}^{10} x_{i}$	$\sum_{i = 1}^{10} y_{i}$	$\sum_{i = 1}^{10} z_{i}$	$\sum_{i = 1}^{10} {(x_{i} - \bar{x})}^{2}$	$\sum_{i = 1}^{10} (x_{i} - \bar{x}) (y_{i} - \bar{y})$	$\sum_{i = 1}^{10} (x_{i} - \bar{x}) (z_{i} - \bar{z})$
275	731.1	21.7	150	2368.36	30

表中 $z_{i} = \ln y_{i}$ ， $\bar{z} = \frac{1}{10} \sum_{i = 1}^{10} z_{i}$

附：对于一组数据 $(u_{1} ， v_{1})$ ， $(u_{2} ， v_{2})$ ， $\dots (u_{n} ， v_{n})$ ，其回归直线 $v = α + β u$ 的斜率和截距的最小二乘估计分别为 $β = \frac{\sum_{i = 1}^{n} (u_{i} - \bar{u}) (v_{i} - \bar{v})}{\sum_{i = 1}^{n} {(u_{i} - \bar{u})}^{2}}$ ， $α = \bar{v} - β \bar{u}$ ．

(1)、根据散点图判断，

y = a + b x

，

y = a + \sqrt{x}

与

y = c_{1} e^{c_{2} x}

哪一个适宜作为

y

与

x

之间的回归方程模型？（给出判断即可，不必说明理由）

(2)、根据（1）的判断结果及表中数据．

①试求 $y$ 关于 $x$ 回归方程；

②已知用人工培养该昆虫的成本 $h (x)$ 与温度 $x$ 和产卵数 $y$ 的关系为 $h (x) = x (\ln y - 2.4) + 170$ ，当温度 $x$ （ $x$ 取整数）为何值时，培养成本的预报值最小？

查看试题解析

20. 已知函数 $f (x) = - x^{3} + 3 x^{2} + 9 x - 8$ .

(1)、求函数 $f (x)$ 的极值；

(2)、若 $x \in [- 3 ， 0]$ 时， $f (x)$ < $c^{2} + c - 1$ 恒成立，求实数 $c$ 的取值范围.

查看试题解析
21. 今年4月23日我市正式宣布实施“3+1+2”的高考新方案，“3”是指必考的语文、数学、外语三门学科，“1”是指在物理和历史中必选一科，“2”是指在化学、生物、政治、地理四科中任选两科．为了解我校高一学生在物理和历史中的选科意愿情况，进行了一次模拟选科. 已知我校高一参与物理和历史选科的有1800名学生，其中男生1000人，女生800人. 按分层抽样的方法从中抽取了36个样本，统计知其中有17个男生选物理，6个女生选历史．
（I）根据所抽取的样本数据，填写答题卷中的列联表. 并根据 $K^{2}$ 统计量判断能否有 $90 %$ 的把握认为选择物理还是历史与性别有关？

（II）在样本里选历史的人中任选4人，记选出4人中男生有 $X$ 人，女生有 $Y$ 人，求随机变量 $ξ = X - Y$ 的分布列和数学期望．（ $K^{2}$ 的计算公式见下） $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，临界值表：

$P (K^{2} \geq k_{0})$

0.25

0.15

0.10

0.05

0.025

$k_{0}$

1.323

2.072

2.706

3.841

5.024

查看试题解析
22. 已知函数 $f (x) = x^{2} - m \ln x$ ， $h (x) = x^{2} - x + a$ ．

(1)、当 $a = 0$ 时， $f (x) \geq h (x)$ 在（1，+∞）上恒成立，求实数 $m$ 的取值范围；

(2)、当 $m = 2$ 时，若函数 $k (x) = f (x) - h (x)$ 在区间（1，3）上恰有两个不同零点，求实数 $a$ 的取值范围．

查看试题解析

$P (K^{2} \geq k_{0})$	0.25	0.15	0.10	0.05	0.025
$k_{0}$	1.323	2.072	2.706	3.841	5.024

$ξ$	0	1	2
$P$	$\frac{P}{2}$	$\frac{1}{2}$	$\frac{1 - P}{2}$