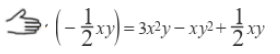初中数学浙教版七年级下学期期中复习专题10 整式的化简及运算
试卷更新日期:2021-04-07 类型:复习试卷
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下面计算 ① ;② ;③ ;④ ;⑤ ; ⑥ .其中错误的个数有( )A、1个 B、2个 C、3个 D、4个3. 若
 ,则
,则  内应填的式子是( ) A、 B、 C、3 D、4. 化简求值:( a4b7+ a3b8﹣ a2b6)÷(﹣ ab3)2 , 其中a= ,b=﹣4.( )A、1 B、﹣1 C、2 D、 ;5. 若M=(x-3)(x-4),N=(x-1)(x-6),则M与N的大小关系为( )A、M>N B、M=N C、M<N D、由x的取值而定6. 已知 ,则整式 的值为( ).A、-3 B、3 C、-6 D、67. 关于x的方程为(x-4)m=x-4且m≠1,则代数式 的值是( )A、36 B、40 C、56 D、688. 若 且 ,则代数式 的值等于( )A、-2 B、0 C、1 D、29. 关于x , y的二元一次方程ax+by+1=-2的一组解为 , 则(a+b-1)(1-a-b)的值为( )A、-16 B、-8 C、8 D、1610. 记 ,则 ( )A、一个偶数 B、一个质数 C、一个整数的平方 D、一个整数的立方
内应填的式子是( ) A、 B、 C、3 D、4. 化简求值:( a4b7+ a3b8﹣ a2b6)÷(﹣ ab3)2 , 其中a= ,b=﹣4.( )A、1 B、﹣1 C、2 D、 ;5. 若M=(x-3)(x-4),N=(x-1)(x-6),则M与N的大小关系为( )A、M>N B、M=N C、M<N D、由x的取值而定6. 已知 ,则整式 的值为( ).A、-3 B、3 C、-6 D、67. 关于x的方程为(x-4)m=x-4且m≠1,则代数式 的值是( )A、36 B、40 C、56 D、688. 若 且 ,则代数式 的值等于( )A、-2 B、0 C、1 D、29. 关于x , y的二元一次方程ax+by+1=-2的一组解为 , 则(a+b-1)(1-a-b)的值为( )A、-16 B、-8 C、8 D、1610. 记 ,则 ( )A、一个偶数 B、一个质数 C、一个整数的平方 D、一个整数的立方二、填空题
-
11. 一个长方形的面积是(x2-9)平方米,其长为(x+3)米,用含有x的整式表示它的宽为米.12. 若x2+4x-4=0,则3(x-2)2-6(x+1)(x-1)的值为 .13. 单项式-x2m-ny3与单项式 可以合并,则多项式4m-2n+(-m-n)2-2(n-2m)2的值是 .14. 在化简求(a+3b)2+(2a+3b)(2a-3b)+a(5a-6b)的值时,亮亮把a的值看错后代入得结果为10,而小莉代入正确的a的值得到正确的结果也是10,经探究后,发现所求代数式的值与b无关,则他们俩代入的a的值的和为 .15. 若(x+2019)(x+2018)=1009,则(x+2019)2+(x+2018)2=。
16. 数a,b,c 在数轴上的位置如图所示.化简:2|b﹣a|﹣|c﹣b|+|a+b|= .
三、计算题
-
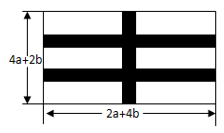
17. 计算题(1)、(2)、(3)、(4)、(5)、20052-2006×200418. 计算:(1)、2(m+1)2+(2m+1)( m-1)(2)、(3)、(3a2b3c4)2÷(- a3 b4)(4)、103×97(利用公式计算)(5)、(6)、-32×(7)、(x-5) 2-(x+5)(x-5)(8)、-3x(2x+5)-(5x+1)(x-2)19.(1)、先化简,再求值: ,其中 , ;(2)、说明代数式 的值与 的取值无关.20. 先化简,再求值(1+a)(1-a)-(a-2)2+(a-2)(2a+1).其中a=- .21. 已知 , ,并且 ,求多项式 .22. 某校为了改善校园环境,准备在长宽如图所示的长方形空地上,修建两横纵宽度均为a米的三条小路,其余部分修建花圃.(1)用含a,b的代数式表示花圃的面积并化简。(2)记长方形空地的面积为S1 , 花圃的面积为S2 , 若2S2-S1=7b2 , 求 的值.
 23. 有这样一道题“计算:(2m4-4m3n-2m2n2)-(m4-2m2n2)+(-m4+4m3n-n3)的值,其中 ,n=-1.”小强不小心把 错抄成了 ,但他的计算结果却也是正确的,你能说出这是为什么吗?24. 长方形的长为a厘米,宽为b厘米,其中 ,将原长方形的长和宽各增加3厘米,得到的新长方形的面积为 ;将原长方形的长和宽分别减少2厘米,得到的新长方形的面积为 .(1)、若a,b为正整数,请说明 与 的差一定是5的倍数;(2)、若 ,求将原长方形的长和宽分别减少7厘米后得到的新长方形的面积.
23. 有这样一道题“计算:(2m4-4m3n-2m2n2)-(m4-2m2n2)+(-m4+4m3n-n3)的值,其中 ,n=-1.”小强不小心把 错抄成了 ,但他的计算结果却也是正确的,你能说出这是为什么吗?24. 长方形的长为a厘米,宽为b厘米,其中 ,将原长方形的长和宽各增加3厘米,得到的新长方形的面积为 ;将原长方形的长和宽分别减少2厘米,得到的新长方形的面积为 .(1)、若a,b为正整数,请说明 与 的差一定是5的倍数;(2)、若 ,求将原长方形的长和宽分别减少7厘米后得到的新长方形的面积.